光流分析中的不连续性

在相互遮挡的物体的轮廓处，会出现光流的不连续（变化）。但是，通过我们前面所讨论的方法（即式(11.40)和(11.41)）所得到的解，在这些轮廓区域处会发生连续的变化。为了克服这个缺陷，我们必须先将这些轮廓区域找出来。这似乎是一个鸡和蛋的问题：如果我们有一个好的光流估计结果，那么，我们可以通过：查找图像中光流发生快速变化的地方，来实现对图像的分割；另一方面，如果我们可以对图像进行很好的分割，那么，我们将可以得到一个更好的光流估计结果。解决这个问题的方法是：将图像分割和光流的迭代求解过程结合在一起，也就是说，在每次迭代以后，我们先查找：图像中光流发生快速变化的地方；然后，我们在这些地方做上标记，以避免在下次迭代时，将这些“光流不连续区域”的解光滑地连接在一起。刚开始时，我们将：判断不连续区域的阈值，设得很高，以避免对图像过早地进行分割；随着光流估计结果越来越好，我们逐渐减小阈值。

对于某些特殊的情况，我们可以分析：关于光流连续性的假设的合理程度。一个常见情况是：物体做刚体运动，包括：平动和转动。为了简单，我们这里使用正射投影模型。对于做平动（并且，我们假设速度方向平行于像平面）的物体，在物体所对应的图像区域中，各个点的光流是相同的。因此，在该区域中，光流的变化是（极其）光滑的。正如我们所预料的，在区域的边界（即：物体“遮挡”背景的地方）上，光流将发生不连续变化。

图11.13　图像序列中相邻的四帧图像。这个图像序列所记录的是：在固定的随机噪声背景下，一个缓慢转动的球。球上覆盖有：光滑变化的亮度模式。我们用光流算法来处理这样的图像序列。

对于转动的理解要稍难一些。首先，我们这里只考虑瞬间量，也就是说，我们只关心：物体坐标在某一时刻的变化率；我们并不去“跟踪”物体在一段时间内的运动。在习题11.6中，我们证明了：物体绕着某一轴转动的过程等价于如下两种运动的“合并”，即：1)物体绕着和这个轴平行并且经过物体中心的轴转动，2)再加上一个平动。这个平动等于：一个从原点到转动轴的向量和旋转向量的叉积。因此，不失一般性，我们可以将转动限制为绕着过原点的轴转。

图11.14　用针状图所表示出的光流估计结果。图中(a)、(b)、(c)和(d)所对应的算法迭代次数分别为：1、4、16和64。

假设物体的转动（速度）由向量w=(α,β,γ)T所确定，其中，向量的长度表示旋转的角速度，并且，旋转轴和该向量的方向一致。物体上某一点的速度等于：从旋转轴指向该点的向量r=(x,y,z)T与给定的转动向量w的叉积。我们使用正射投影，因此，图像坐标x′和y′分别等于物体的坐标x和y。光流中的分量u和v分别等于：物体上的点在x—轴和y—轴方向上的速度分量，即：(www.xing528.com)

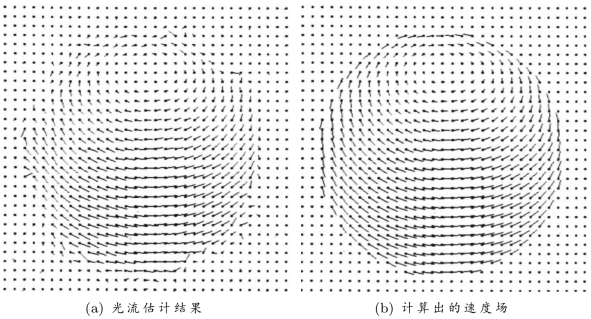
图11.15　(a)迭代算法所得到的光流估计结果。(b)根据物体运动计算出来的速度场。

此时，判断光流的不光滑程度就变得十分简单了，我们可以得到：

对于光滑弯曲的物体表面，在其轮廓附近，曲面的斜率（即：向量(zx,zy)T）趋于无穷大，因此光流将不再光滑。此外，绕着光轴的旋转（即：w=(0,0,γ)T），会增加光流的“光滑性”。

光流计算方法的一个重要应用是无源导航。在无源导航问题中，我们必须根据从环境中收集的信息，来控制某种交通工具的路径和姿态变化。并且，在收集信息的过程中，我们并没有从交通工具中发射辐射信号。我们将在第12章中详细讨论这个课题。