习题10.1请证明:下面3个二阶偏导数算子
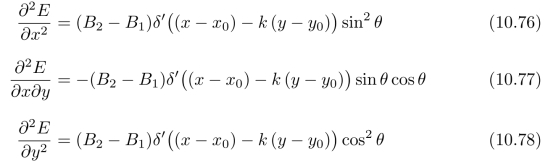
不满足旋转不变性。
进一步,我们想通过上面三个线性算子的线性组合:
![]()
来构造出一个满足旋转不变性的二阶线性偏微分算子,也就是说,与θ无关,请确定上式中参数a、b和c的值。最终,我们证明了:Lap lace算子是满足旋转不变性的唯一的二阶线性偏微分算子。
习题10.2连续图像上的噪声并不是一个非常简单的概念。但是,它对于分析:用于进行边缘提取的算子的连续形式,却是非常有用的。假设我们所处理的噪声的波形为n(x,y),其均值为0,也就是说,对于整个图像区域R,我们有:

同时,我们假设:噪声的波形在图像中不同点的值,可以被看作是:独立的随机变量;并且,在不同的图像区域中,噪声具有相同的“功率”。假设:在给定的区域R中,噪声波形的自相关函数为:
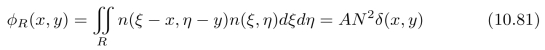
其中,A为区域R的面积。注意,自相关函数和区域面积之间存在线性依赖关系。这个结果是合理的,因为,我们希望:在半个图像区域中所计算出的结果,独立于在另外半个图像区域中所计算出的结果。因此,当我们将这两个随机变量加在一起时,和的方差等于各个随机变量的方差的和。
式(10.81)中的N 2确定了:噪声在单位面积上的“功率”大小。注意,单位面积上的真实功率是无穷大的,这是因为我们所处理的“信号”,其频谱是“平的”,也就是说,噪声的带宽是无穷大。只有限制频带宽度,我们才能使得:噪声在单位面积上的“功率”是有限的。我们可以让噪声通过一个低通滤波器,来实现这个目的。
(a)我们感兴趣的是:噪声通过一个点扩散函数为h(x,y)的滤波器后,在单位面积上的功率。滤波后的噪声的平方的积分为:
![]()
其中,o(x,y)=n(x,y)⊗h(x,y)。证明:滤波器输出结果的平方的积分(即:式(10.82))为
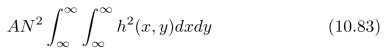
注意:噪声的滤波结果不再是不相关的了,但是,这并不影响:我们计算噪声波形的平方的积分。
(b)我们让一张图像通过一个Gauss平滑滤波器,该滤波器的点扩散函数为:
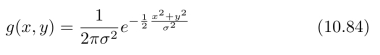
请问:输出结果中,单位面积上的噪声的功率是多少?随着σ的变化,这个结果将发生什么变化?请考虑:当σ→0时的极限情况。
习题10.3在这个问题中,我们将比较:三种边缘增强算子的“表现”。对于每一种情况,我们都先使用Gauss函数(即:式(10.84))和图像做卷积,从而减小噪声的影响;然后,使用微分算子来“突出”高频分量。这三种算子分别为:1)一阶方向导数,2)二阶方向导数,3)Laplace算子(它是一个旋转对称算子)。我们将探索:每一个算子对于阶梯函数(即:信号)和随机噪声的响应。我们使用:信号波峰值与噪声的均方根的比值(即:PSNR),来衡量每一种算子的“表现”。令:
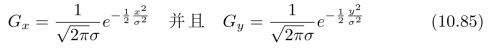
于是,旋转对称的Gauss函数G可以表示为Gx和Gy的乘积,即:G=Gx Gy。或者,我们也可以令:
![]()
此时,G可以表示为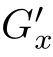 和
和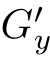 的卷积,即:G=
的卷积,即:G=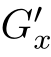 ⊗
⊗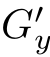 。同时,我们还需要注意的是:对Gauss函数与图像的卷积结果进行求导运算,等价于:Gauss函数的导数与图像的卷积。这是由于求导是一个:线性移不变算子,因此,这两个算子(即:求导和卷积)是可交换的。
。同时,我们还需要注意的是:对Gauss函数与图像的卷积结果进行求导运算,等价于:Gauss函数的导数与图像的卷积。这是由于求导是一个:线性移不变算子,因此,这两个算子(即:求导和卷积)是可交换的。
我们可以使用:相应的点扩散函数,来表示三种算子,即:
![]()
我们的测试函数选为:单位阶梯函数,它的边缘经过原点,即:
![]()
我们也可以将单位阶梯函数E(x,y)看作:

其中δ是单位无限冲击函数。
(a)对于单位阶梯函数,请判断:式(10.87)中的每一种算子的响应。提示:在第6章中,我们曾经介绍过:求导和积分可以看作:某一恰当的广义函数的卷积。注意:这些算子是可交换的!注意到这一点,可以大大简化我们的工作,例如,你可能不会想要去:求出式(10.87)中的三种算子所对应的点扩散函数的显式格式。
(b)使用式(10.87)中的每一种算子,所得到的边缘增强图像中,最大值和最小值所对应的点各是什么?在这三张边缘增强图像中,有两张应该具有相同的极值点。
和上一题一样,我们使用如下积分:
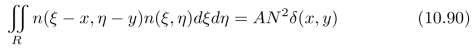
来表征图像的噪声,那么,在边缘增强结果中,单位面积上噪声的功
率为:
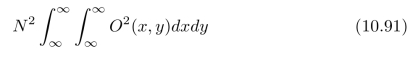
其中O(x,y)是:算子的点扩散函数。
(c)对于式(10.87)中的每一种算子,请计算:1)它们各自所对应的噪声的方差,以及,2)信号峰值和噪声的均方差的比值。在这里,均方差正好是方差的平方根。如果算子的“尺度”σ是固定的,那么,三种算子中,哪一种表现最好?哪一种最差?
(d)信噪比依赖于:算子的“尺度”σ。要使得式(10.87)中的第一种算子的信噪比等于第三种算子的信噪比,那么,第一种算子的“尺度”σ,应该是第三种算子的多少倍?
习题10.4对于一张理想的、直的单位阶梯边缘的图像,使用Lap lace-Gauss级联滤波器对其作用以后,所得到的“跳变零”点,正好位于边缘上。这里,我们将探索:当边缘是一条曲线时,将发生什么情况?考虑一个理想的圆盘图像,即:
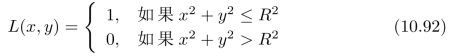
在该图像与Lap lace-Gauss级联滤波器的卷积结果中,如果存在“跳变零”点,那么,这些“跳变零”点一定形成一个圆,这是因为:图像和算子都是旋转对称的。请判断:由“跳变零”点形成的圆,其半径是否为R?如果不是,那么其半径是否接近于R?是否存在由其他半径的“跳变零”点所形成的“假的”圆?
提示:计算Gauss函数与圆盘的卷积,是非常困难的,但是,我们可以使用如下事实:Lap lace算子和Gauss卷积是可交换的。
习题10.5请使用Tay lor展开式来证明:下面三个模板
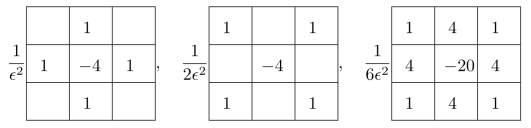
所产生的结果分别为:
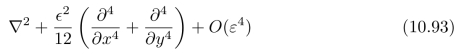
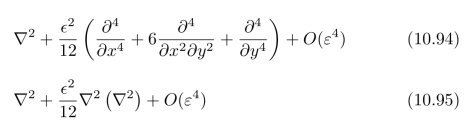
其中∇2表示:Lap lace算子。
习题10.6证明:如果我们用一个失焦的成像系统对一条理想的边缘进行成像,那么,所得到的“模糊”边缘的亮度b(x)为:(https://www.xing528.com)
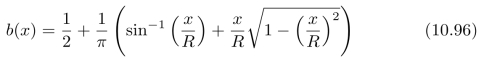
其中,|x|<R,并且,我们使用竖直朝向的单位阶梯函数作为输入,此外,我们假设模糊核(即:一个圆)的半径为R。记住:模糊核的积分一定等于1,这是因为:能量只是被分散了,并没有凭空产生或消失。进一步,请证明:边扩散函数的最大斜率等于b(x)的高和宽的比值再乘以4/π。
提示:边扩散函数是对线扩散函数的积分。
习题10.7如果我们要生成一个独立于坐标系的尺度输出,那么,旋转对称算子是非常有用的。我们已经介绍过一些旋转对称算子,包括:梯度的平方、二次变分和Laplace算子。另一个有用的概念是:与坐标系无关的向量。这种向量的模长与坐标系的选取无关;并且,向量所在的方向,相对于曲面来说是固定的。亮度梯度就是一个与坐标系无关的向量。
(a)假设:从点(x,y)到点(x′,y′)之间的变换为:
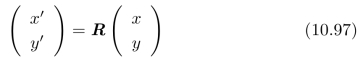
其中,矩阵R是一个正交的旋转矩阵,即:

并且,c2+s2=1。请证明:
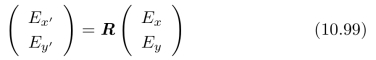
(b)证明:(Ex,Ey)T是一个与坐标系无关的向量。请通过(Ex,Ey)T推导出:一个旋转对称的尺度。
(c)现在证明:
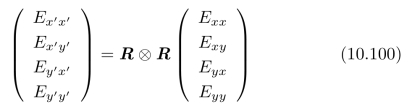
其中,R⊗R是:旋转矩阵R与其自身的K ronecker积,即:
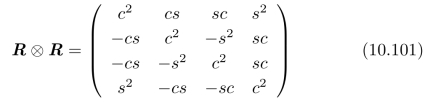
(d)由此,我们可以进一步推断出:向量
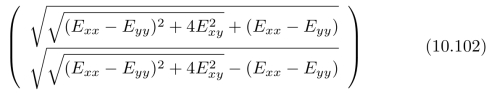
是一个与坐标系无关的向量。请通过该向量,推导出一个旋转对称的尺度。
(e)请将:一阶和二阶与坐标系无关的向量组合在一起,推导出:两个旋转对称的尺度。提示:使用点积,然后将其中一个向量旋转90°,从而获得第二个尺度。
(f)证明:如果(a,b)T和(c,d)T都是与坐标系无关的向量,那么,(a2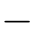 b2)(c2
b2)(c2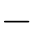 d2)+4abcd和(a2+c2)(b2+d2)都是旋转对称的尺度。
d2)+4abcd和(a2+c2)(b2+d2)都是旋转对称的尺度。
(g)由此,我们可以得出:下面的两个量![]()
![]() 都是旋转对称的。
都是旋转对称的。
习题10.8在某些情况下,我们希望检测图像中的直线,而不是边缘。例如,一个有趣的课题是:将工程图转化为符号形式,以便于计算机辅助设计(CAD)系统对其做进一步处理。这种情况下的“线”是指:具有低亮度的一维曲线。因此,不同于前面介绍的问题,即:寻找一阶导数的极值或二阶导数的“跳变零”点,我们这里所寻找的是:亮度的极值或一阶导数的“跳变零”点。
(a)请解释:为什么对于这种情况,寻找Ex=0和Ey=0的边缘检测器无法取得好的效果?
提示:如果亮度极小值沿着直线方向不是常数,会如何?
(b)我们可以将E(x,y)看作一个三维空间中的曲面。请证明:最速上升的方向为如下单位向量,即:
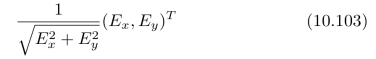
并且,沿着该方向的方向导数为:![]() 。
。
(c)请求出:使得二阶方向导数取得极值的两个方向。你可以用两个单位向量来表示这两个方向。证明:这两个方向之间的夹角是90°;并且,它们所对应的二阶方向导数的极值分别为:
![]()
提示:在练习3.5中,我们求得了:2×2的实对称矩阵的特征值和特征向量。
(d)我们现在需要确定:我们所寻找的线的中心点。我们可以求出:1)最速上升的方向,以及,2)二阶方向导数的最小值所对应的方向。使得这两个方向平行的点,就是我们所要找的中心点。请解释为什么我们可以这么做。
(e)请设计一个非线性算子,用来检测问题(d)中所定义的中心点。
(f)当图像区域的亮度为常数时,或者,当亮度随着x和y而发生线性变化时,你在上一问中所导出的算子将会有什么问题?请设法解决这个问题。
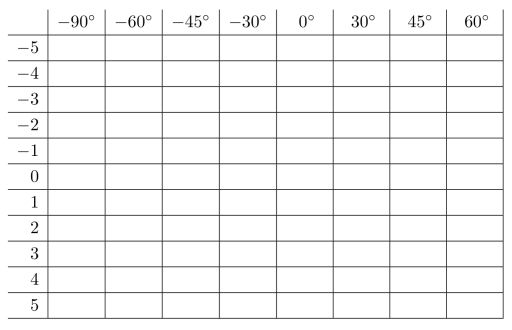
习题10.9本题中,我们将通过对简化模型的计算,来深入理解Hough变换。假设边缘检测结果构成一个4×4的二值图。请针对下面给出的4种情况逐一进行分析。
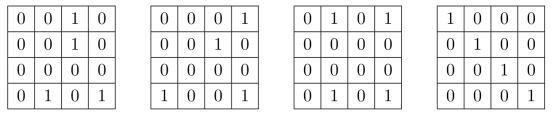
我们将ρl的11个取值设定为{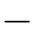 5,
5, 4,···,0,1,···,5};将θn的8个取值设定为{
4,···,0,1,···,5};将θn的8个取值设定为{ 90°,
90°,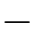 60°,
60°,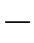 45°,
45°, 30°,0°,30°,45°,60°}。相应地,Hough变换统计结果Nn,l构成一个11×8的矩阵,对应于下面的表格。请完成Hough变换的计算,填写下表。
30°,0°,30°,45°,60°}。相应地,Hough变换统计结果Nn,l构成一个11×8的矩阵,对应于下面的表格。请完成Hough变换的计算,填写下表。
习题10.10对于下面的二值图,请通过计算查找边缘和角点。

(a)请计算:式(10.25)中的P rew itt算子所得到边缘增强图像,进而给出Prew itt算子的边缘检测结果。
(b)请计算:式(10.28)中的Sobel算子所得到边缘增强图像,进而给出Sobel算子的边缘检测结果。
(c)分别选用4×4、5×5、6×6的窗口进行Harris角点检测,对所得到的结果进行对比分析,完成实验报告。

图10.13 Horn教授在《Robot V ision》中文版中题写的“致广大中国读者”。
习题10.11本题中,我们来探索一个具有挑战性的问题:对小图像区域进行拼接。一张写了文字的纸张,被碎纸机切割成许多形状规则的“小纸片”。我们将所有的“小纸片”收集起来后,希望能够通过算法,复原出纸张上的文字内容。图10.13中给出了Horn教授在《Robot Vision》中文版中题写的“致广大中国读者”[4],我们以这张图像为例,来进行实验。首先,我们将图10.13切割成一系列的“小方块”,如图10.14(a)所示;然后,对这些“小方块”进行随机排列,参见图10.14(b)。我们要探索的问题是:如何根据图10.14(b)复原出图10.13?显然,在这个任务中,边缘和角点发挥着重要作用。

图10.14 碎纸机对(写了文字的)纸张的处理过程和结果。
【注释】
[1]参见:D.Marr,V ision:A com putational Investigation in to the Hum an Represen tation and Processing ofV isual Inform ation,1982.
[2]在数值计算过程中,ρm只能取一系列的离散值(例如:取整数值),此时,ρm=![]() 应该相应地调整为ρm=
应该相应地调整为ρm=![]() ,其中
,其中![]() 表示“四舍五入”操作。
表示“四舍五入”操作。
[3]注意,沿着边缘法线方向的方向导数为:
[4]参见:《机器视觉》,Berthold K.P.Horn(著),王亮、蒋新兰(译),中国青年出版社。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




