平行轴旋转定理解析

注意，在二值图分析的章节中，我们在计算图像区域的朝向时，首先，将旋转轴移动到了区域的中心，然后，计算图像区域绕着该轴旋转时的转动惯量。最小和最大转动惯量的比值，给出了图像区域形状的一种描述。比值越接近0，图像区域的形状越接近一条直线；比值越接近1，图像区域的形状越接近一个圆。

在上一小节中，我们用了上面的结论来设计角点检测算法，但是，我们并没有将旋转轴移动到梯度空间中二值图的中心，而是让旋转轴过原点。注意：图像中的一组平行的边缘对应于：梯度空间中一条过原点的直线。图10.9中所示的梯度空间中的一条不过原点的直线，对应着很多条不平行的边缘，因此，图像区域中存在角点（如果图像区域足够小）！

下面，我们将通过数学分析，说明两种不同情况：1)将旋转轴移动到梯度空间中二值图的中心和2)让旋转轴过原点，之间的关系。

图10.9　边缘图像并不是对应于梯度空间中的一条直线，而是对应于梯度空间中的一条过原点的直线。梯度空间中的一条不过原点的直线，对应着很多条不平行的边缘，因此，图像区域中存在角点。

我们令为梯度空间中二值图的中心，也就是说，

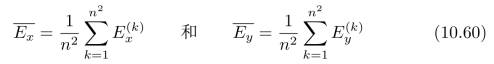
于是，式(10.51)可以被进一步写为：

我们令：(www.xing528.com)

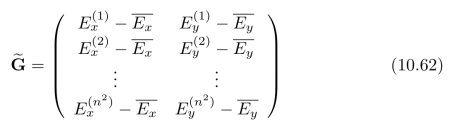
进一步，我们令：

于是，式(10.52)可以被进一步写为：

上式又被称为：平行轴旋转定理。对于任意给定方向u=(c,s)T，当旋转轴过原点时，转动惯量为u T S u；当旋转轴过中心时，转动惯量为u T S u。因此，两者之间的关系为：

对于图10.9中的情况，当u=(c,s)T恰巧平行于图中的直线方向时，u T S u=0，但是，u T S u=。只有当图10.9中的直线过原点时，对于所有的图像亮度梯度(Ex,Ey)T，才有Ex c+Ey s=0，也就是说，；此时，u T S u=0。这种情况所对应的图像小块正好是边缘。因此，在上一小节中，我们通过：分析矩阵S的两个特征值之间的关系，来实现角点检测，而不是去分析矩阵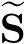 S的特征值。