如何进行角点检测？

多条边缘汇聚的地方被称为角点，参见图10.6。角点虽然是局部特征，但是却不能通过前面介绍的局部微分算子，例如：梯度算子、Laplace算子等，来直接进行计算。“多条边缘”这几个字本身就暗示着：无法通过一个点来进行观察和计算；“汇聚”这两个字暗示着：观察的区域不需要太大。

10.5.1　角点的判断标准

上述分析为我们提供了一个检测边缘的思路：判断某一个图像小块里面是否存在两条或者两条以上不平行的边缘。但是，这并不完善，即使图像小块中存在两条或者两条以上不平行的边缘，这些边缘也不一定相交；即使这些不平行的边缘相交，也不一定只有一个交点；即使这些不平行的边缘相交于一点，这一点也不一定在图像区域内部，可能在图像区域外面。但是，只要我们选择的图像小块足够小，上面的那些可能性就将不复存在。因此，

•只要在足够小的图像块中存在两条以上不平行的边缘，那么，图像小块中就一定存在角点！

图10.7　图像亮度的梯度给出了边缘点的法向方向，因此，我们只需要分析图像小块内部各个像素点的图像亮度梯度，看看是否存在多个法向方向，即可实现角点检测。

前面关于边缘检测的分析为我们进一步查找角点提供了基础，我们只需将其直接应用于图像小块中的像素点即可。图像亮度的梯度(10.12)给出了边缘点的法向方向，在边缘检测过程中，我们已经计算出了各个像素点的图像亮度梯度，因此，我们只需要分析图像小块内部各个像素点的图像亮度梯度，看看是否存在多个法向方向，即可实现角点检测，如图10.7所示。

注意，我们所要确定的，是图像小块中是否存在不同的法向方向，而不是去判断图像小块中是否存在不同的法向量。因此，我们不能直接通过：对（边缘检测过程中所得到的）图像亮度梯度做统计，来判断图像小块中是否存在角点。对于要分析的n×n图像小块，我们将其中所有n2个像素的图像亮度梯度列写成一个n2×2矩阵：

事实上，矩阵G中的每一行，都是“Ex—Ey空间”中的一个点。我们将“Ex—Ey空间”称为梯度空间。因此，矩阵G对应着梯度空间中的一个二值图，如图10.8所示。我们可以将在二值图相关章节中学习到的分析方法应用过来。在图像小块中，每一条边缘片段上的所有点的图像亮度梯度都位于：梯度空间中的某一条直线附近。因此，如果图像小块中存在角点，梯度空间中的二值图至少分布在两条直线附近，如图10.8所示。

图10.8　图像小块中每一个像素点的亮度梯度(Ex,Ey)，都对应于“梯度空间”中的一个点。图像小块中所有像素点的亮度梯度，就构成了梯度空间中的一个二值图。

10.5.2　角点检测算法

至此，角点检测问题被转化成了：梯度空间中的二值图形状分析问题。在前面关于二值图的章节中，我们分析过类似问题：通过计算二值图绕着过原点的轴旋转所产生的转动惯量，来判断二值图的形状。在这里，我们可以采用相同的方法来进行分析，首先计算：(www.xing528.com)

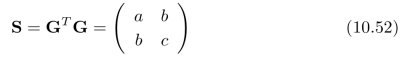
其中，

如果矩阵S的两个特征值λ1和λ2的比值接近于0，那么图10.8中的二值图接近于一条过原点的直线。此时，图像小块内只有平行的边缘，不存在角点。因此，矩阵S的两个特征值λ1和λ2的比值是区别边缘和角点的一个重要指标。最终，我们得到了下面的两个标准：

来确定图像小块中是否存在角点，其中T和η为设定的阈值，我们令λ1≤λ2。注意，条件λ1＞T已经保证了λ2/=0。由于需要对图像中的所有图像小块进行遍历，因此，我们希望每一个图像小块的计算都能尽量简洁。由于特征值的计算过程较为复杂，即：

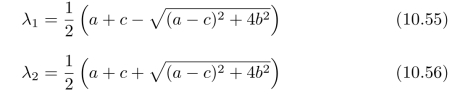
我们需要对式(10.54)中的标准做一些优化。由于

可以很容易地通过矩阵S直接计算出来。因此，Harris提出使用

来判断图像小块中是否存在角点，参数k的取值一般设为0.04到0.06之间。上述方法被称为Harris角点检测算法。当然，还有其他的判断方法。注意，式(10.54)分别给出了特征值λ1和λ2的算术平均值和几何平均值，我们可以用两者比值的平方来作为判断标准，也就是说，

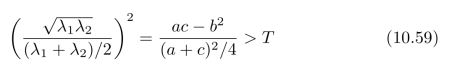
上式中用到了除法运算，从计算的角点考虑，做除法不如做减法，也就是说，不等号两边同乘以(a+c)2/4，再移项进行整理。于是，我们又回到了Harris判断标准(10.58)。