如何确定图像边缘生成原因？

经过边缘增强以后，如果所得到的信号（边缘增强图像）比噪声大得多，那么，我们可能会推断出：图像中的某一点是否位于边缘上。但是，这个推断并不一定可靠，因为噪声可能恰巧使得：这一点和周围的点之间出现显著的差别。

10.4.1　边缘检测和定位

我们所能做的是：选择一个阈值来对边缘增强图像做二值化处理，从而减少“假的边缘点被接受”的情况所发生的概率。如果阈值选得太大，那么，一些弱的边缘会被忽略掉。因此，我们需要在两种误差之间选择一个平衡。在边缘检测过程中，通过增加用来取平均值的小图像块的尺寸，我们可以减小噪声的影响，从而使得“弱的”边缘更容易被检测处理。我们可以从频率域来考虑这个问题，小图像块的尺寸越大，对应的低通滤波器的截止频率就越低，因此，增加用来取平均值的小图像块的尺寸，等价于：增加被抑制的频域范围。但是，我们又必须面对另一个取舍问题，在抑制噪声和定位边缘之间取得一种平衡。因为，如果小图像块中包含多个边缘，那么，所得到的边缘检测结果是不可靠的。我们注意到：短的边缘必须具有更大的对比度，才能够被检测出来！

经过边缘增强的图像，并不是只有边缘上的点有很大的值，边缘附近的点也有很大的值。如果为了去噪，我们预先对图像进行了“光滑”处理，那么，这种现象会更加明显。因此，这就产生了边缘定位的问题。如果不考虑噪声，我们可以期望：（在边缘增强图像中）边缘上的点取得局部最大值。这些局部最大值可以被用于：抑制边缘点附近的“很大的”值的影响。

如果我们使用梯度平方算子进行边缘检测，那么，在经过边缘增强的图像中，每一条边缘处都有一个“山脊状”突起，其大小与该边缘两侧的亮度差成正比。对于Lap lace算子和二次变分的情况，边缘处会有两条平行的“山脊状”突起，这两条“山脊状”突起分别位于边缘两侧。对于Laplace算子，这两条“山脊状”突起的方向是相反的（即：一条是凸出，一条是凹陷），我们可以将边缘定为：这两条“山脊状”突起的方向发生变化的地方。

10.4.2　简单边缘模型的缺陷

经过边缘检测，我们所定位的是：（图像中的）一些边缘点，还不是一条条完整的边缘。事实上，根据检测出的边缘点来生成边缘并不是一个简单的任务。为此，我们必须明确：引起边缘的物理原因。被边缘检测器所检测出的图像亮度的快速变化，是由三维场景中的哪些“因素”产生的？到目前为止，我们关于这方面还知之甚少。人们已经意识到了简单边缘模型的局限性，并且，已经提出了很多更加符合实际情况的边缘模型。

简单边缘模型将边缘看作是：理想阶梯函数加噪声。许多边缘检测方法所共有的一个问题是：它们所基于的前提假设通常并不符合实际情况。尽管许多物体表面具有相同的反射率，但是，这些物体表面所形成的图像却不一定具有相同的亮度；相反地，对应于不同物体表面“小块”的像素点，其灰度值却可能非常相似，参见图3.2。只有在极其特殊的情况下，我们才可以将图像看作是：由一组具有“一致亮度”的区域所组成的集合。对边缘检测方法的评估是很困难的，这其中的一个原因是：我们缺乏对任务的明确定义。我们如何辨别：边缘是否被“漏掉了”，或者，“伪边缘”出现在什么地方？这些问题的答案依赖于：我们要用边缘检测的结果来做什么？

我们在第1章的图1.13中所给出的例子，就形象地说明了上面所谈到的一些问题。图1.13(a)所显示的是：一个用积木搭建起来的简单场景所生成的图像。图1.13(b)显示的是：一个边缘查找器对该图像的输出结果。即使对于这种简单的情况，边缘查找器所检测到的边缘“碎片”也是不完美的。要将这些边缘“碎片”组合成：用来描述物体轮廓的清晰的线条图，还有许多细致的处理工作要做。图1.13(a)中物体的轮廓对应于图1.13(b)中的长直线，我们的任务逐渐变得明确了：如何根据（二值）图1.13(b)中的边缘点来确定长直线边缘？

10.4.3　确定长直线边缘

对于一些极其特殊的情况，我们可以探索如何确定图像中的边缘。本节中，我们讨论一种特殊的情况：根据检测出的边缘点，确定图像中长直线形状的边缘。我们以第2章中的图2.2为例，详细说明：根据图2.2(a)生成图2.2(b)的具体过程。首先，通过本章介绍的Sobel算子，我们共检测到了64409个边缘点，如图10.5(a)所示。

进一步，我们需要判断：（图10.5(a)中的）某一个边缘点p m=(xm,ym)T位于哪一条直线上。我们需要两个参数θn和ρl来指定一条直线：

参见图7.10。直线经过点p m的意思是：(xm,ym)T满足式(10.47)，也就是说，表达式

成立。给定点p m，我们无法确定直线的参数θn和ρl，但是，我们却可以轻易地判断：图10.5(a)中的某一个点在哪一条直线上。我们是如何做到的呢？虽然图10.5(a)中过某一个点有很多p m的直线{sn,l}，但是，在其中的一条直线sn′,l′上，有大量的点。“有大量的点”这几个字的具体意思是：有很多点{(xi,yi)T}都满足式(10.47)。于是，我们得到了寻找直线的一种方法：

•首先，对于每组给定的直线参数θn和ρl，将所有的边缘点{(xi,yi)T}逐一地代入式(10.47)，验证其是否成立；

•然后，统计（代入边缘点过程中）式(10.47)成立的次数；(www.xing528.com)

•如果成立次数大于给定阈值，则判定（由参数θn和ρl确定的）直线sn,l是一条直线形边缘，否则，判定直线sn,l不是边缘。

如果我们生活在Pau l Hough的时代（20世纪60年代），相信我们也能设计出相应的直线查找方法，但是，和Hough的工作比起来，上述方法还有一个明显的差距：存在计算冗余。假设边缘点(xi,yi)T对于式(10.47)不成立，在上述过程中，计算结果被直接舍弃了。事实上，计算结果中是包含更多有用信息的，通过计算，我们不仅知道：边缘点(xi,yi)T不属于参数为θn和ρl的直线，进一步，我们还知道：边缘点(xi,yi)T属于某一条参数为θn和的直线，其中=xi cosθn+yj cosθn，进一步，我们还知道，对于某一个固定的参数θn，边缘点(xi,yi)T只属于这一条直线。

为了提升计算效率，我们可以将上述过程中的“验证式(10.47)（对于直线参数θn和ρl）是否成立”变为：对于某一个固定的θn，计算使得边缘点(xi,yi)T代入后成立的参数：然后直接得出结论：对于某一固定的参数θn，边缘点(xi,yi)T只属于某一条参数为θn和ρm=的直线，对于剩下的一系列参数{ρl}l/=m都不成立。总结起来，一次计算取代了一系列验证过程。经过上述优化调整，我们就得到了是著名的Hough变换：

•首先，对于每一个给定的θn，将所有的边缘点{(xi,yi)T}逐一地代入，根据式(10.49)计算出，对应参数θn和ρm=的计数器Nm,n增加一次计数^[2]：Nm,n=Nm,n+1；

•然后，遍历所有的θn，统计出每一条直线sn,l（边缘点代入后）的成立次数N l,n；

•如果成立次数大于给定阈值，则判定（由参数θn和ρl确定的）直线sn,l是一条直线形边缘，否则，判定直线sn,l不是边缘。

图10.5(b)中给出了：根据（图10.5(a)中的）边缘点而得到的Hough变换统计结果N l,n，其中，l为行标，从1到1801，对应的ρl从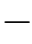1800到1800，间隔为2；n为列标，从1到900，对应的θn从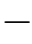90°到89.8°，间隔为0.2°。图10.5(a)中的亮度对应于N l,n的数值，其最大值为720。

Hough变换的统计结果N l,n给出了：直线sn,l上的边缘点数目。只有拥有足够多边缘点的直线，才被认为是直线形边缘。因此，我们可以对N l,n设置一个阈值，从而选取相应的直线形边缘。图10.5(c)中给出了：通过判断标准N l,n＞400选取出的206组直线参数。每一组直线参数对应于一条直线，图10.5(d)中画出了对应的206条直线，就是根据图10.5(a)中的边缘点所确定出的长直线边缘。对比图10.5(a)和10.5(d)，我们可以进一步观察：这些直线形边缘与边缘点之间的对应关系。图10.5(d)进一步验证了我们在第2章2.2小节中得出的结论：空间中一组平行直线的像都相交（或汇聚）于消失点。

我们可以进一步“筛选”图10.5(a)中的边缘点，只保留位于长直线上的点，如图2.2(b)所示。边缘点(xi,yi)T到直线ln,l的距离为：

如果边缘点(xi,yi)T到所有长直线的距离都大于某一阈值（例如4个像素点距离），则将其舍弃。最终，图2.2(b)中只保留了38413个边缘点，占图10.5(a)中边缘点总数的59.64%。

注意，Hough变换图像10.5(b)与CT扫描图像2.15(a)很相似。这并非偶然，事实上，Hough变换就是在对二值图做CT扫描！

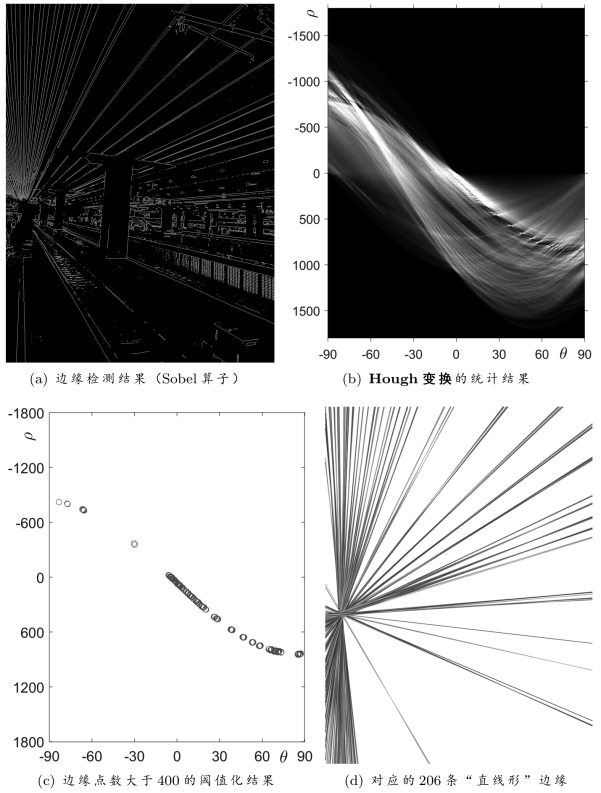
图10.5　我们可以通过Hough变换，来（根据边缘点）确定对应的“直线形”边缘。(a)Sob el算子对图2.2(a)的边缘检测结果，共检测出64409个边缘点。(b)根据边缘点得到的Hough变换统计结果N l,n，其中，ρl从-1800到1800，间隔为2；θn从-90°到89.8°，间隔为0.2°。(c)我们可以对N l,n设置一个阈值，从而选取相应的直线形边缘。通过判断标准N l,n＞400，总共选取出了206组直线参数。(d)每一组直线参数对应于一条直线，对应的206条直线就是检测出的直线形边缘。

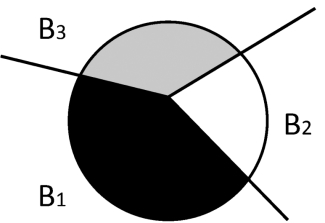
图10.6　多条边缘汇聚的地方被称为角点。“多条边缘”这几个字本身就暗示着：无法通过一个点来进行观察和计算；“汇聚”这两个字暗示着：观察的区域不需要太大。