求解函数k(σ)和光滑化算子的点扩散函数形状——习题解析

习题9.1求函数k(σ)的表达式，使得当δ→0时，下面的函数族：

定义了一个单位冲击函数。

习题9.2考虑下面的函数族：

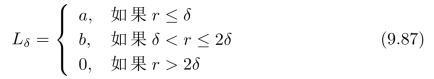
其中r=。当a和b取什么值时，这个函数族定义了一个：对应于Laplace算子的广义函数？也就是说，在什么情况下，Lδ和f(x,y)的卷积的极限等于∇2 f(x,y)？

提示：你可能会想将该算子作用于函数：

式(9.88)中的函数f(x,y)的Lap lace算子处理结果等于1。

习题9.3证明：如果一个矩阵可以被分解为两个向量

的外积，也就是说，，那么，矩阵

的（二维）离散Fou rier变换结果F(p,q)，也可以被分解为两个向量f1和f2的（一维）离散Fourier变换结果的乘积，并且，其中一个是关于p的函数，而另一个是关于q的函数，也就是说，F(p,q)=F1(p)F2(q)。

习题9.4证明：如果≥0对于所有的x和y都成立，那么，对于所有的p和q，都有F(0,0)≥|F(p,q)|。请问：什么时候F(0,0)=F(p,q)？

习题9.5通常，对于一个用于进行“光滑化”处理的算子，其点扩散函数的“形状”为：1)在原点(x,y)=(0,0)处，点扩散函数的值最大；2)在其他点处，点扩散函数的值都为正，并且，随着x和y趋于无穷，点扩散函数的值衰减到0。为了方便，我们可以将这样的点扩散函数，看作一种质量分布。不失一般性，我们假设：该质量分布的中心位于原点处。我们必须能够描述：这个质量分布的“分散情况”。一个质量分布的回转半径是：一个到质心的距离，具体地说，如果我们将该质量分布的全部质量集中在：到质心的距离等于回转半径的质点上，那么，该质点所产生的转动惯量等于：原来的质量分布（所产生）的转动惯量。质点的转动惯量等于：质点的质量与该质点到原点的距离平方的乘积。

质量分布h(x,y)的总质量M为：

我们令：r2=x2+y2，于是，回转半径R的定义为：

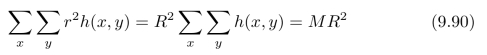
(a)求：圆柱体的回转半径，其中，圆柱体的定义为：

(b)求Gauss函数的回转半径，其中，Gauss函数为：

注意：(a)和(b)中的分布都具有“单位质量”；并且，将式(9.90)中的积分转化为：极坐标下的积分形式，可能会有助于求解。

(c)证明：两个函数的卷积的质量，等于这两个函数的质量的乘积。同时证明：两个函数的卷积的回转半径的平方，等于这两个函数的回转半径的平方和，也就是说，如果f=h*g，那么，其中，Rf、Rg和Rh分别为：f、g和h的回转半径。

(d)如果一个旋转对称的光滑函数和“自身”进行多次卷积，那么，所得到的卷积结果将变得和Gauss函数及其相似。假设：式(9.91)中的函数和自身卷积n次，那么，其对应的近似Gauss函数的标准差σ是多少？

习题9.6证明：a★(b*c)=(a★b)*c。其中，符号★表示相关；而*表示卷积。

习题9.7一个光学望远镜的调制传递函数为：

其中：P(p,q)是一个旋转对称的低通滤波器：

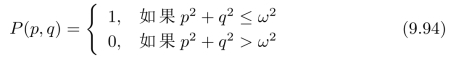
其中，截至频率ω取决于：入射光的波长以及光学器件的尺寸。

(a)两个半径相同的圆，当它们的圆心不重合时，公共部分的面积是多少？

(b)求A(p,q)。

(c)相应的点扩散函数是什么？

习题9.8考虑一个图像模糊系统，该系统的点扩散函数为：标准差为σ的Gauss函数。假设：噪声的功率谱是平的，功率为N 2；信号的功率谱也是平的，功率为S2，并且，S2＞N 2。此外，我们假设：噪声是在图像模糊以后加上去的。(www.xing528.com)

(a)请给出：去除图像模糊的最优滤波器所对应的调制传递函数。

(b)该调制传递函数的低频响应是什么？

(c)放大倍数最大的频率成分是什么？

(d)该最优滤波器的最大增益是多少？

习题9.9让我们来考虑如下的两张图像：

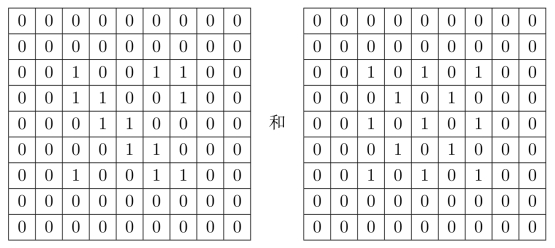
(a)对于如下的Gauss模糊核：

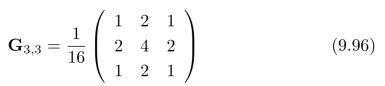
上面两张二值图模糊后的结果是什么？

(b)请解释如下的运动模糊核：

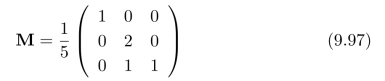
进一步，请计算：上面两张二值图经过运动模糊后的结果。

(c)请解释如下的均匀模糊核：

进一步，请计算：上面两张二值图经过均匀模糊后的结果。

(d)我们选用W iener滤波器进行图像复原，当参数τ=Φnn/Φbb选取为不同的值时，例如τ=0.1,0.01,0.001,0.0001，对应的图像复原结果是什么？请编写程序进行计算机仿真，然后，根据仿真结果完成实验报告。

习题9.10本题中，我们将探索图9.2中的圆柱形光斑所对应的离散图像，也即是说^[3]，在离散二值图中生成一个“圆”。

(a)首先，生成圆的边缘，假设圆的半径为r，也就是说，

于是，离散二值图中“圆”就是一系列整数对(xn,yn)，满足：

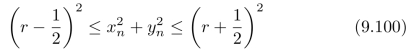
其中xn和yn都是整数。对于0°到45°的那段圆弧，我们可以通过求解：

来进行查找，参见图9.12。请分析式(9.100)和(9.101)之间的关系，进一步，根据图9.12设计出整数对(xn,yn)的查找算法。

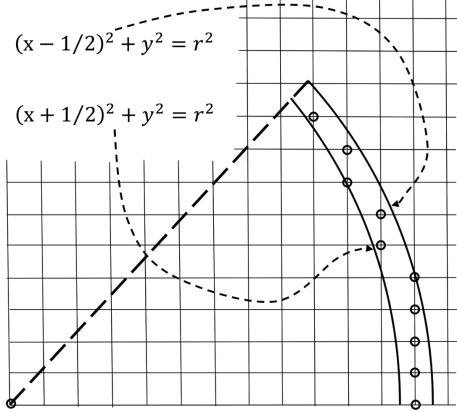
图9.12　对于0°到45°的圆弧，可以通过求解式(9.101)来“查找”整数对(xn,yn)。

(b)式(9.101)告诉我们：在算法执行过程中，需要“跟踪”参数：事实上，我们只需要跟踪一个参数τ1≤0，即可实现数据的迭代更新，请完成理论分析。

(c)对于45°到90°的圆弧，应该如何处理？请完成离散圆生成算法。

(d)对于尺度较小的光斑（例如10×10个像素），我们可以采用如下策略：首先，生成一个大尺度的光斑（例如100×100个像素）；然后，将大尺度光斑划分为一系列相同大小的“小区块”（包含10×10个像素）；最后，对“小区块”取平均，就得到了尺度较小的光斑。请设计程序实现上述操作，完成实验报告。

【注释】

[1]参见图14.7中的子图14.7(a)和14.7(d)。这样的噪声也称为白噪声。这个名称是非常形象的。白光是所有颜色的的光混杂在一起形成的。如果包含所有的频率成分，就会呈现出白色；否则，就会（由于某些频率成分的缺失而）呈现出其他颜色。

[2]在离散Fou rier变换结果中，高频成分位于“中心”位置，低频成分位于“四周”位置，参见式(9.24)。对变换结果做“平移”，就是将低频成分“移动到”中心位置，高频成分“移动到”四周位置，MatLab自带命令“あtshift”用于完成这一操作。

[3]参见论文：B.K.P.Horn,“Circle Generators for D isp lay Devices,”Com pu ter Graphics and Im age Processing,Vol.5,No.1,June 1976,pp.280-288.