如何生成离散Gauss模糊模板及其Wiener滤波器处理结果

上面两节中，我们针对连续情况进行了理论分析，本节中，我们将讨论相应的离散情况，包括两部分内容：1.离散Gauss模糊所对应的模板，2.数字图像的Gauss模糊过程与相应的W iener滤波器。

离散Gauss模糊所对应模板的生成方式并不是：直接对式(9.32)中的二维Gauss分布进行离散采样。这主要有两方面的原因：1.离散采样后，权重系数的和并不等于一；2.有更加方便简洁的方式来近似计算二维Gauss分布的离散形式（参见习题8.5）。

通常，我们可以用“二项式分布”来近似给出：式(9.32)中二维Gauss分布的离散采样结果，其背后的原理是中心极限定律。一维Gauss分布可以被采样为：一个含有n个元素的向量g n。向量g n中的元素对应于：多项式(1+z)n-1/2n-1的系数。例如，当n=5时，

相应地，二维Gauss分布的离散采样结果Gn为：两个一维Gauss分布采样结果g m和g n的外积，也就是说，

例如，当m=n=5时，

为了便于观察，我们将G5,5“放置”在一个21×21的全零矩阵的中心位置，如图9.8(a)所示。我们让G5,5与自身做卷积，得到了一个新的二维Gauss分布的离散采样结果：G9,9=G5,5*G5,5。同样地，我们将9×9的矩阵G9,9“放置”在一个21×21的全零矩阵的中心位置，如图9.8(b)所示。

我们对图9.8(a)做离散Fou rier变换，然后对变换结果做“平移”^[2]，所得到结果的幅度也近似为Gauss函数的离散形式，如图9.8(c)所示。我们继续对图9.8(b)做离散Fourier变换，然后对变换结果做“平移”，所得到结果的幅度也近似为Gauss函数的离散形式，如图9.8(d)所示。图9.8中的结果验证了我们前面的结论：空间域的尺度越大，对应的频率域的尺度就越小；反之亦然。

图9.9是数字图像的Gauss模糊以及相应的W iener滤波器处理结果。图9.9(a)所示的是原始清晰图像（包含21×21个像素点），图像亮度归一化为0到1之间。图9.9(b)所示的是模糊加噪声的图像，模糊核为图9.8(a)所示的5×5的离散Gauss模板；加性噪声设置为0到0.1之间的随机数。我们将式(9.76)中的Φn n/Φbb设置为0.01。此时，W iener滤波器的复原结果如图9.9(c)所示，边缘和角点得到了锐化，但是，噪声被明显地放大了。作为对比，我们将式(9.76)中的Φn n/Φbb设置为0.1。此时，W iener滤波器的复原结果如图9.9(d)所示，噪声被有效抑制住了，但是，边缘和角点的锐化效果不佳。当然，我们可以进一步对W iener滤波器做改进，例如，T ikhonov正则化方法将式(9.76)中的Φn n/Φbb替换为关于(p,q)的函数λ×(p2+q2)。

让我们来看一个算例，考虑如下3×3的离散Gauss核：

我们用该离散Gauss核来对：图像中“棋盘格”形状的二值图区域，进行模糊化模拟。将下面的6×6的“棋盘格”图像区域

图9.8　二维离散Gau ss模糊核及其离散Fou rier变换。(a)将G5,5“放置”在一个21×21全零矩阵的中心位置。(b)G5,5的自卷积结果G9,9。(c)图9.8(a)的离散Fou rier变换“平移”后的结果。(d)图9.8(b)的离散Fou rier变换“平移”后的结果。(www.xing528.com)

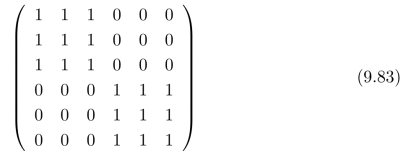
图9.9　图像的Gau ss模糊以及W iener滤波器的复原效果。(a)原始清晰图像，包含21×21个像素。(b)模糊加噪声的图像，Gauss模糊核如图9.8(a)所示。(c)信噪比设置为0.01时的图像复原结果。(d)信噪比设置为0.1时的图像复原结果。

与3×3的离散Gauss核进行循环卷积后，得到的模糊图像为：

图9.10　棋盘格图像的模糊和复原过程。

模糊图像中，边缘和角点都变得难以分辨，如图9.10(b)所示。采用W iener滤波器(9.76)进行复原，信噪比设为0.01，复原结果为：

较之于模糊图像9.10(b)，复原图像9.10(c)中的边缘和角点更清晰。

很多时候，我们往往并不知道Gauss模糊核的实际大小，图9.11中给出了一个具体例子。图9.11(a)中给出了对应的模糊图像，包含6 81×421个像素点。在使用W iener滤波器进行图像复原的过程中，我们需要设置两组参数：1)Gauss模糊核Gm,n的大小m×n，2)信噪比的倒数τ=Φnn/Φbb（参见式(9.75)）。图9.11(b)和9.11(c)中给出了选取33×33的高斯模糊核所得到的图像复原效果，参数τ分别设为0.005和0.0001。此时，图像复原效果并不明显，并且，在τ=0.0001时，图9.11(c)中明显出现：（噪声放大所引起的）“细碎状波纹”。

通过对比图9.11(d)、9.11(e)和9.11(f)，我们发现：随着（所选取的）高斯模糊核的尺寸不断增大，复原图像变得越来越清晰。另一方面，当所选取的高斯模糊核过大时，图像中（边缘附近的）“伪影”现象变得十分严重（参见图9.11(f)）。

图9.11　在使用W iener滤波器进行图像复原时，选取不同参数所得到的结果。其中，Gm,n表示：大小为m×n的Gauss模糊核，τ=Φn n/Φbb表示：信噪比的倒数。

当然，我们也可以将图中的多张复原图像“融合”在一起，从而形成一张“更好”的图像。要解决这个问题，首先需要给出一个合理的评价标准，用来确定复原图像的好坏。对于实际应用，我们却并没有原始图像用来做参考，因此，找到一个合理的评价标准并不是一件容易的事。到目前为止，这仍是一个开放性的问题，有待于大家的进一步探索。在习题9.9我们还将继续探索更多的图像模糊形式，例如：运动模糊和均匀模糊，以及对应的图像复原结果。