提高信号清晰度的Wiener滤波器优化

本节将探讨最优滤波器，W iener的研究工作奠定了最优滤波器的理论基础。1966年，W iener在他的著作《Extrapolation,Interpolation,and Smoothing ofStationary Time Serieswith Engineering Applications》中，通过一个绝妙的关于Fourier变换的对称定义，使用变分法导出了最优滤波器，也称为W iener滤波器。

本小节中，我们针对连续情况进行理论分析，得出一般性结论。在最后才给出离散化的算法处理方式。假设我们所得到的测量结果中包含：信号b(x,y)与加性噪声n(x,y)，也就是说，我们所得到的是b(x,y)+n(x,y)；任务是尽可能地复原出信号b(x,y)，如图9.7所示。

9.8.1　优化模型

我们用：处理结果o(x,y)和理想信号d(x,y)的差的平方的积分，也就是说，

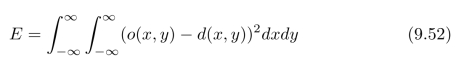
来作为衡量处理结果好坏的标准。通常，d(x,y)就是b(x,y)，如图9.7所示。我们需要最小化式(9.52)。我们之所以选择最小化误差平方的积分（最小二乘法），是因为在数学上容易进行处理。如果我们使用一个线性系统来进行滤波操作，那么，我们可以通过点扩散函数h(x,y)来描述这个系统。系统的输入为：

系统的输出为：

将式(9.54)代入(9.52)中，我们可以得到：

由于o2=(i⊗h)2，我们可以进一步计算：

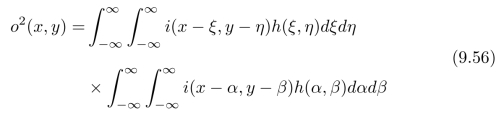
首先，将式(9.56)中的两个二重积分的乘积化为一个四重积分；然后，交换积分次序，即：先对x和y积分，再对其他变量积分；最后，我们可以进一步得到：

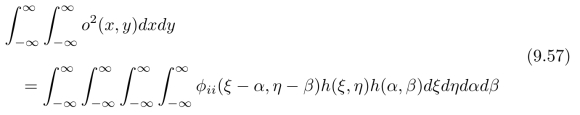
式(9.57)中的ϕii(x,y)是函数i(x,y)的自相关。此外，

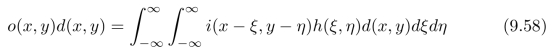
因此，

其中，ϕid(x,y)是函数i(x,y)和d(x,y)的互相关。最后，我们有：

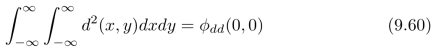
其中，ϕdd(x,y)是函数d(x,y)的自相关。

现在，我们可以将误差平方项的表达式(9.55)写为：

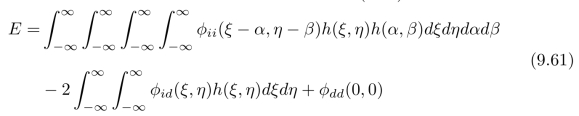
我们将在下一小节中介绍：如何通过寻找一个“最好”的点扩散函数h(x,y)来最小化式(9.61)。

9.8.2　变分法求解

求解式(9.61)是一个变分问题，我们将使用变分法来解决这个问题。在传统的微积分（特别是有关最优化的）问题中，我们所要寻找的是一个参数值，通过这个参数值，我们可以计算出函数的值。而在这里，我们所需要寻找的是一个函数，通过这个函数，我们可以计算出某个给定泛函的值。

泛函是一个依赖于函数的表达式，例如，式(9.61)中的E依赖于函数h(ξ,η)。我们假设：函数h(x,y)使得E取得最小值，那么，无论δh(x,y)的形式是什么，由函数h(x,y)+ϵδh(x,y)所确定的泛函值E+δE，都不能比E小。其中，δh(x,y)表示任意函数，用以对函数h(x,y)进行调整。如果h(x,y)真的使得E取得最小值，那么，对于任意函数δh(x,y)，都有：

否则，我们可以通过将h(x,y)换为h(x,y)+ϵδh(x,y)。新的函数h(x,y)+ϵδh(x,y)会使得E的值减小。这与我们的假设（即：h(x,y)使得E取得最小值）是矛盾的。现在，我们计算式(9.62)，即：

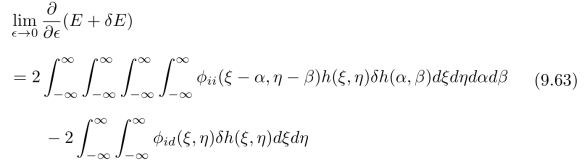
我们可以将上式进一步整理为：

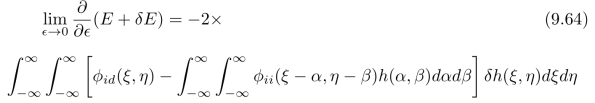(www.xing528.com)

极值条件（即式(9.62)）意味着：对于所有的δh(x,y)，式(9.64)的结果都等于零。要满足这个条件，在式(9.64)中，中括号里面的表达式必须等于零，也就是说，

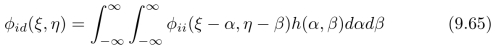
也就是说：

（或许你会对这个结果感到惊讶）。我们可以通过Fou rier变换，来求解上面这个关于h(x,y)的简单表达式，也就是说，

其中，Φii和Φid是功率谱。因此，我们只需要知道功率谱，就能设计出（基于给定假设的）图像复原系统。对于某“一类图像”来说，这个系统都是最优的。注意：我们并不知道d(x,y)，因此，无法计算ϕid和Φid。但是，我们可以赋予d(x,y)一些约束条件，从而对“一类图像”进行描述。

9.8.3　两个具体例子

首先，让我们来考虑第一个例子：设计一个噪声抑制系统，也就是说，系统的输入是：图像b(x,y)与噪声n(x,y)的和；系统的目标是：产生一个（在最小二乘意义上）尽可能和原始图像b(x,y)接近的输出o(x,y)。对于这个问题，d(x,y)=b(x,y)，并且，

根据Φii和Φid的定义，我们可以得到：

并且：

我们假设：信号与噪声不相关，那么，Φbn=Φn b=0。于是，

Φbb/Φn n被称为信噪比。从式(9.71)中可以清楚地看出“最优系统”所做的操作：对于信噪比很高的频率成分，系统的增益几乎等于1，而对于噪声占主导的频率成分，系统的增益非常低、接近于信噪比。

现在，让我们来考虑另外一种情况：信号b(x,y)首先经过一个点扩散函数为h(x,y)的系统，然后，再被加上噪声n(x,y)，也就是说，

我们希望设计一个点扩散函数为h′(x,y)的系统，使得式(9.72)中的信号i(x,y)经过该系统的作用以后，所得到的输出结果为：

和原始图像b(x,y)（在最小二乘的意义上）尽可能地接近。对于这个

问题，d(x,y)=b(x,y)，因此，

并且，

假设噪声和信号无关，即：Φbn=Φn b=0，于是，我们可以得到：

对于信噪比很高（也就是说，Φbb/Φnn很大）的频率成分，

但是，对于Φn n＞|H|2Φbb的频率成分，系统的增益

这个结果和我们前面用“启发式方法”所导出的结果，即式(9.42)和(9.43)，具有一定的相似性。