图像失焦导致的频率衰减和复原问题

对于一个成像系统而言，我们发现，根据理想成像模型本应该汇聚到一点的那些光线，事实上会轻微地扩散开来，形成一个小光斑。这种图像模糊可能会有多种形式，但是，我们有时可以使用：具有单位体积的Gauss点扩散函数，来对其进行建模，即：

由于式(9.32)中h(x,y)的值依赖于x2+y2，而不是单独依赖于x和y，因此，式(9.32)中的Gauss点扩散函数是一个旋转对称的函数。我们可以使用Hankel变换来计算其Fou rier变换，但是，由于Gauss函数的特殊性，我们可以采用更加简单方法，来计算其Fou rier变换。

注意，式(9.32)中的Gauss函数正好可以被分解为：两个函数的乘积，并且，这两个函数分别为：一个关于x的函数和一个关于y的函数。因此，我们可以先将二重求和分解为：两个一重求和的乘积，然后，再进行计算。这样做可能会更容易计算一些。

首先，我们来计算式(9.32)中的Gauss函数的Fourier变换：

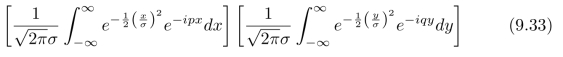
式(9.33)中的第一个积分等于：

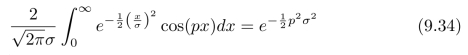
因此，我们最终得到了：

与我们所预料的一样，上式也是旋转对称的。

注意观察式(9.35)，我们注意到，低频信号得以通过，而对于频率的模长（即：大于1/σ的高频信号，其幅度得到很大的衰减。因此，我们可以将σ作为：对Gauss点扩散函数的“分散大小”的一种测量，因此，模糊越大，能通过式(9.35)中的滤波器的低频信号的频率范围就越小。我们不难发现：空间域的尺度变化和相应的频率域的尺度变化成反比。事实上，如果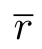是空间域上的有效半径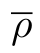，是对应频率域上的有效半径，那么，它们的乘积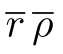是一个常数。

图像模糊的一种情况是失焦。在这种情况下，光线的汇聚点并不在像平面上，而是在像平面靠前或靠后一点的位置上。相应的点扩散函数为一个小圆柱，如图9.1所示。从镜头发出并且汇聚于空间中某一点的所有光线，会形成一个圆锥，这个圆锥与像平面相交，会形成一个圆斑，这个圆斑就是：图像失焦所对应的点扩散函数。在这个圆斑内，亮度是一致的，如图9.2所示，因此，我们可以得到：(https://www.xing528.com)

这里，

其中，d是透镜的直径、f′是透镜到聚焦点的距离、e是聚焦点到像平面的距离。使用Hankel变换，我们可以得到：

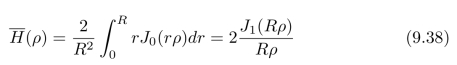
其中，J0(z)和J1(z)分别表示零阶和一阶Bessel函数。可以证明：

因此，在原点处取得最大值；然后，缓慢地在rB=3.83171···处衰减到零；然后，为负值；然后；再以衰减的振幅增大到零，如图9.4所示。对于二维系统，函数J1(z)/z所起的作用类似于：函数sin(x)/x在一维系统中所起的作用。函数J1(z)/z的振幅的渐近衰减速率为z-3/2。

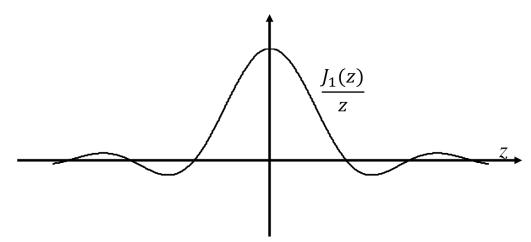
图9.4　二维系统中，函数J1(z)/z所起的作用类似于：函数sin(x)/x在一维系统中所起的作用。和函数J1(z)/z做卷积，输入信号中频率高于截止频率的频率成分会被系统“吃掉”，也就是说，点扩散函数为J1(z)/z的系统是一个理想的低通滤波器。

同样，低频分量得以通过式(9.38)中的滤波器，高频分量的幅度会得到很大的衰减，有些频率分量则完全不能通过该滤波器。由于J1(z)围绕水平面振荡，因此，一些频率成分发生“变号”。对于J1(z)＜0的频率成分，失焦图像中最亮的部分，对应于理想图像中最暗的部分；反之亦然。

使得J1(z)=0的频率成分则完全被系统“吃”掉了。从失焦图像中，我们无法对这些频率成分进行复原。正如我们前面所提到的，J1(z)的第一个零点为z=3.83171···。我们再一次发现：频率域的尺度变化和空间域的尺度变化成反比关系，也就是说，失焦半径R越大，使得J1(Rρ)=0的频率ρ就越小。

事实上，时间上的周期变化对应于频率，空间上的周期变化对应于波长，波长乘以频率等于波速。波速只和材料的性质有关，可以被看作一个常量。因此，对于在同种材料中传播的波，如果频率变为原来的k倍，那么，波长一定会变为原来的1/k。从这个角度出发，我们不难理解：频率域的尺度变化总是和空间域的尺度变化成反比。