线性移不变系统的特性与应用

图像可以被看作一个二维信号，以矩阵的形式进行存储。图像处理系统将一张图像转换成另一张新的图像，也就是说，将一个矩阵变成另一个新的矩阵。对于图9.1所示的一张失焦图像，如果像平面的位置合理，成像系统将场景中的每一个点，都汇聚到了图像上相应的像素点；如果像平面的位置不合理，成像系统将场景中的每一个点，都汇聚到了图像上相应的光斑，最终得到的图像是所有这些光斑的叠加，因此，图像会变得模糊。

我们可以用线性系统来对上述过程进行建模。系统的输入为：一张理想的对焦图像f={fi,j}，系统的输出是：对应的失焦图像g={gk,l}，线性系统将对焦图像f={fi,j}变为失焦图像g={gk,l}，称为图像退化。我们将在下一小节中详细讨论图像退化过程的数学模型，本节中，我们着重弄清楚一个基本概念：线性移不变。

假设f={fi,j}是由准确聚焦的成像系统所生成的图像。现在，如果我们改变光照条件，使得理想图像的亮度变为原来的两倍，那么，失焦图像的亮度也将变为原来的两倍。进一步，如果我们将成像系统稍稍移动一下，使得理想图像在像平面上轻微地移动一下位置，那么，失焦图像也将会做类似的移动。我们将从理想图像到失焦图像之间的变换，称作是一个线性移不变的操作。事实上，对于许多非相干光学图像处理系统，通常情况下，它们是线性移不变的（尽管它们的结构更加复杂）。

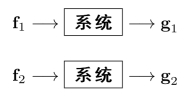
下面，我们将会给出一个关于线性移不变的更精确的定义。假设：当一个系统的输入为f1和f2时，系统的输出分别为g1和g2，也就是说，

如果对于任意α和β，当系统的输入为αf1+βf2时，系统的输出都为αg1+βg2，也就是说，

那么，我们称这个系统是线性的。

在实际应用中，大多数系统的最大输出值的大小都是有限的，因此，这些系统并不是严格线性的。

现在，让我们来考虑一个系统，当系统的输入为f={fi,j}时，系统的输出结果为g={gk,l}，也就是说，(www.xing528.com)

如果对于任意a和b，我们先将系统的输入移动(a,b)T；然后，将移动后的结果{fi-a,j-b}输入系统，此时，系统所产生的输出结果正好为{gk-a,l-b}，即：{gk,l}移动(a,b)T所得到的结果，也就是说，

那么，我们称这个系统是移不变的。

在实际情况中，图像的大小是有限的。因此，系统的移不变性质往往只是近似成立的。

对于理解成像系统的性质来说，掌握对线性移不变系统的分析方法是非常重要的。成像系统的缺陷常常被看作是一个线性移不变系统。该系统将一张理想图像变为我们所观察到的图像。

一个关于线性移不变系统的简单例子是：产生输入图像在“水平”和“竖直”方向上的差分。容易验证，该系统是线性移不变的。在后面的章节中，我们将会看到：对于边缘检测来说，这个差分系统是一个非常重要的预处理阶段。在我们运用针对一维信号的强大处理方法的同时，我们也必须指出其不足。线性移不变这个约束条件虽然方便了理论分析，但是，也极大地制约着图像处理操作的种类。

图9.2　对于图像失焦，点扩散函数h(x,y)的形状是一个“小圆柱体”。一个单位的能量意味着函数h(x,y)具有单位体积。