离散二维系统的卷积问题：习题优化

习题8.1一个二维离散系统的特征表现在：它的点扩散函数{hij}。假设：一个系统的输出{gij}和输入{fij}之间的关系满足：

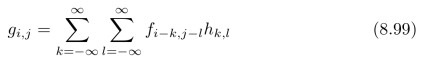
求系统的调制传递函数：{hij}的Fou rier变换结果。

提示：系统的调制传递函数是离散的吗？是周期函数吗？

习题8.2假设有一个离散二维系统，它的表现是一个卷积（正如我们在上一题中所看到的）。现在假设：系统的输入是噪声，也就是说，每一个fij都是：均值为0、方差为σ2的独立随机变量。

(a)系统的输出gij的均值和方差是什么？

(b)所有的点扩散函数都必须满足下面的约束条件，即：

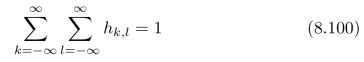
我们希望：系统输出中所包含的噪声最小。请问：应该选取什么样的点扩散函数？

(c)对于满足约束条件

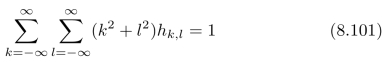
的所有的点扩散函数，哪一个使得系统的输出中所含有的噪声最小？

提示：你可能会想要使用Lagrang乘子，将约束条件加入到优化表达式中。

习题8.3考虑Lap lace算子的离散近似形式。我们使用如下的模板（即：权重系数模式）：

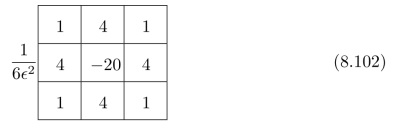
其中，ϵ是：图像单元（即：像素点）之间的距离。请将：式(8.102)中的权重系数模式，写为：9个无限冲击函数的和的形式。然后，请求出：其对应的Fou rier变换。进一步，请证明：当ϵ→0时，式(8.102)在原点附近（即：当u2+v2很小的时候）的Fou rier变换结果趋近于：(u2+v2)。

习题8.4考虑上一题中所使用的Lap lace算子的离散近似形式。对（模板的）中心点处的图像亮度进行Tay lor展开，并且，将(8.102)中的权重系数模式代入到Tay lor展开式中。请证明：最终所得结果与常数项和线性项无关。并且，进一步证明：上述过程所得到的结果是：我们所期望得到的二阶项的组合。同时，请求出：误差项的最小阶数。

习题8.5本题中，我们将建立一种：幂级数与离散点扩散函数之间的有用关系。同时，我们将展示一种：使用离散滤波器来逼近Gauss滤波器的方法。考虑两个多项式f(x,y)和g(x,y)。

(a)证明：由多项式的乘积f(x)g(x)的各项系数所组成的系数序列等于：多项式f(x)和g(x)这两个系数序列之间的卷积。请将这个结论进一步扩展为：包含x的负幂项的情况。

我们可以将上面的结果推广到二维情况，也就是说，乘积f(x,y)g(x,y)的系数序列等于：多项式f(x,y)和g(x,y)的（这两个）系数序列之间的二维离散卷积。注意，此时的“系数序列”应该排列成一个矩阵。此外，还需注意的是：根据二维离散卷积的性质，我们可以直接得出如下结论，即：幂级数的乘法满足结合律和交换律。现在，让我们来考虑一个具体的例子，即问题(b)。

(b)证明：如果在一个卷积过程中，滤波器的权重系数模式为：

那么，该卷积可以被分解为：两次卷积。并且，在这两次卷积过程中，滤波器的形式是相同的，其权重系数为：

使用式(8.104)中的2×2的权重系数模式来进行3次卷积，那么，我们可以通过一次卷积，来得到：这三次卷积所得到的结果，请问：这个等效的一次卷积的权重系数模式是什么？

(c)证明：我们只需要将幂级数中的x换为e-iuw、将y换为e-ivh，就可以得到：幂级数的系数所对应的离散滤波器。

(d)请问：和多项式1+x+y+xy所对应的卷积滤波器的Fou rier变换是什么？

通过(1+x)n的展开式，我们可以得到一个特别重要的多项式：

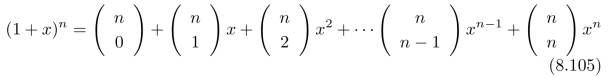
其中，二次项系数为：

(e)我们可以通过：(d)中的滤波器和它自身卷积n次，从而得到：一个二维的二项式分布，其通项为：

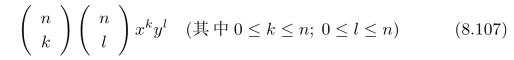(www.xing528.com)

证明：上式的调制传递函数的幅度为：

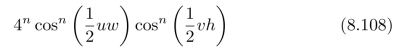
如何消除式(8.108)中的系数4n？通过何种操作，我们可以使得：所得到的调制传递函数为实数（至少当n为奇数时）？

(f)n阶二项式分布近似于：均值为(n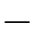1)/2、方差为2n-1的Gauss函数。Gauss函数的幅度为2n-1。n阶二项式分布的调制传递函数也近似于一个Gauss函数。请求出：式(8.108)所逼近的Gauss函数的幅度、均值和方差。

当我们想用（有限大小的）离散滤波器来近似表示Gauss函数时，上面的分析是很有用的。

习题8.6请分析下面3个模板的意义，也就是说，用下面三个模板和图像做卷积，分别起到什么作用？

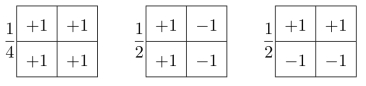
上面三个模板分别和下面的图像做卷积，得到的结果是什么？

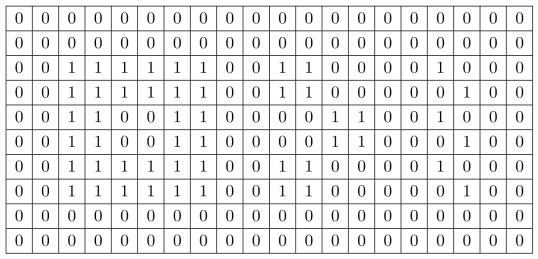
上面的三个模板依次和图像做卷积，得到的结果是什么？请根据计算结果进行理论分析，完成实验报告。

习题8.7本题中，我们来看一个具体的算例：图8.8中的例子。请计算输入图像经过CT扫描后所得到的结果，以及（CT扫描所生成的）数据阵列在经过后向投影以后，所得到的输出图像。系统的输入图像选为下面的“三角形”二值图：

(a)请分析后向投影算法的具体实现过程。给出算法的伪代码描述形式，然后，编写程序实现算法。

(b)根据第2章的习题2.10中的分析，对本题中给出的输入图像进行CT扫描，给出实验仿真结果。例如：当方向采样精度选为Δθ=π/100时，所得到的CT扫描结果如图8.8(c)所示。

(c)进一步，请给出对（经过CT扫描所得到的）数据阵列的后向投影结果，如图8.8(b)所示。

(d)不难看出，“图像处理系统”的输入图像8.8(b)是对输入图像8.8(a)的模糊化结果，可以“近似”描述为一个卷积过程。请依据图8.8中的结果，分析卷积核的特征。进一步，请根据输入图像8.8(a)和输出图像8.8(b)，来确定卷积核的具体形式。

(e)在第2章的习题2.10中，我们研究了一个极其特殊的情况：只存在一个“金属点”P=(x0,y0)T。在习题2.10中，我们通过求解线性方程组，来寻找“金属点”P的位置。我们能否通过后向投影来寻找“金属点”P的位置？如果能，应该如何查找？

图8.9　图像可以被显示在一个半球面上。对应的“像素”点并不是均匀地分布在半球面上。我们需要想办法让这些“像素”点均匀（或尽量均匀）地分布在球面上。

(f)当扫描区域中存在两个或多个“金属点”时，我们在第2章的习题2.10中介绍的寻找“金属点”位置的方法，是否能让有效？如果无效，我们应该如何对其进行修正？我们能否通过后向投影来寻找这些“金属点”的位置？如果能，请给出具体实现方法；如果不能，请说明理由。

提示：你可能会想要参见第7章习题7.10中的分析过程。

习题8.8除了（我们平时常见的）以矩阵形式显示出来的图像以外，我们还可以通过多种不同的形式来显示一张图像。例如，在图8.9中，图像被显示在一个半球面上。

(a)如果仔细观察，你会发现：图8.9中的“像素”并不是均匀地分布在半球面上。请问：能否让这些“像素”均匀地分布在半球面上？如果能，应该如何操作？如果不能，请说明理由。

(b)事实上，图8.9中的每一个“像素”点，都对应着一个方向。我们之所以要让这些“像素”点均匀地分布在半球面上，是为了对探测方向进行均匀采样。这具有非常大的应用价值，因此，不管能否让这些“像素”点均匀地分布在半球面上，我们都要想办法让这些“像素”点均匀（或尽量均匀）地分布在半球面上。请设计具体的实现方法。

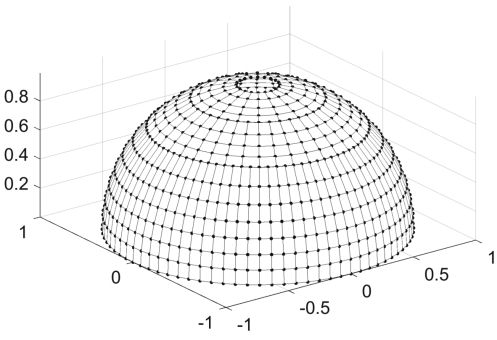
图8.10　要实现对探测方向进行均匀采样，并不是一个简单的问题。

(c)在此基础上，请进一步探索：如何将习题8.7中研究的CT扫描和后向投影过程，拓展到图8.9所示的半球面上图像的情况？

提示：这个问题并不简单。可以在图8.10的基础上做进一步探索。

【注释】

[1]“Tep litz”这个词还是Horn教授最早告诉我的，他的出生地Tep litz-Sch¨onau小镇，就是为了纪念这位伟大的数学家而命名的。

[2]向量a和向量x中的元素个数可能不同，但是，我们可以通过“补充”0的方式，强行使得：向量a和向量x中的元素个数相同。

[3]注意，W n是一个对称矩阵，因此，对于所有的k=0,1···,n-1，都有W n(z k◦)=z k◦W n成立。

[4]置换矩阵中的P 0和P 1只更换向量中元素的位置，较之于乘法运算，上述操作的工作量可以直接被“忽略”。