深入理解卷积定理的多项式角度

两个向量a和b经过相互作用，从而生成一个新的向量。这并不是我们非常熟悉的“操作”。这两个向量之间可以进行内积，但是其结果是一个数a T b。这两个向量之间可以进行外积，但是其结果是一个矩阵ab T。前面所讨论的卷积和循环卷积，其结果是一个向量。从线性代数或矩阵论的观点来看，卷积的生成方式为：用其中的一个向量a来生成一个矩阵A=(a*)，然后矩阵A乘以向量b得到一个新的向量A b=a*b。当然，通过向量a来生成一个矩阵A的方式有很多，例如，我们可以定义如下的A=(a◦)：

也就是说，将向量a中的各个元素逐一地“放到”矩阵A的对角线上。于是，我们可以将两个向量a和b之间的线性运算定义为：

也就是说，两个向量a和b中对应元素相乘所得到的向量，也称为：向量a和b的点乘。首先，点乘满足交换律，也就是说，

我们可以通过点乘来描述离散Fou rier变换矩阵W n中各个列向量之间的关系，也就是说，

此外，式(8.11)中的循环卷积矩阵A c可以被表示为：

进一步，根据点乘的性质，我们可以计算^[3]：将式(8.14)代入，最终，我们得到了如下结论：

注意，W n y、W n a和W n x分别是y、a和x的离散Fou rier变换结果。我们令：

于是式(8.59)可以被进一步写为：

或者进一步写为：

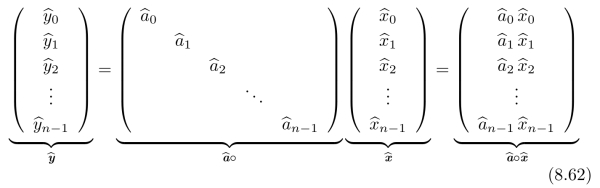
对比式(8.14)和(8.61)，我们得到了卷积定理：

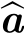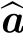•两个向量a和x的循环卷积a⊗x对应于：这两个向量的离散Fou rier变换结果（ a和 x）的点乘 a◦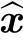 x。反之亦然。

最后，我们可以从多项式的角度来深入理解卷积定理。事实上，式(8.60)中的离散Fou rier变换结果是：多项式在（wn=1的解锁对应的）n个点上的离散采样。离散Fourier变换结果之间的点乘等价于：多项式的乘积在（wn=1的解锁对应的）n个点上的离散采样。从这个角度出发，卷积定理在说：多项式之间的乘积对应于多项式系数之间的卷积；反之亦然。事实上，这个结论是显然的，参见习题8.5。

想想我们计算乘法的过程，例如；312×564。我们在小学三年级学的乘法运算法则背后的原理是：将多项式的乘积(2×z0+1×z1+3×z2)×(4×z0+6×z1+5×z2)展开，再对系数进行归并。由于z3=1，归并的结果为：(2×4+1×5+3×6)z0+(2×6+3×5+1×4)z1+(2×5+1×6+3×4)z2。相应的多项式系数正好是：相乘的两个多项式的系数的循环卷积。

8.5.1　特征值分析

熟悉线性代数的朋友可能会一眼看出：式(8.58)事实上是矩阵的特征值分解形式。我们对式(8.58)的等号两端进行转置，可能更容易

看出这一点，也就是说，

其中，

是一个对角矩阵。在特征值分解中，我们常将对角矩阵D记为Λ，称为矩阵A Tc所对应的特征值矩阵；而离散Fourier变换矩阵W也称为：矩阵A Tc所对应的特征向量矩阵。离散Fourier变换矩阵W实现了对矩阵A Tc的对角化，也就是说，

于是，从特征值分析的角度，我们将离散Fou rier变换和卷积定理联系在了一起，也就是说，

进一步，我们可以得到：

这正好是式(8.61)中给出的卷积定理的结论。

8.5.2　快速Fourier变换

在本小节的最后，我们来谈一下离散Fourier变换（DFT）的快速计算方法：快速Fou rier变换（FFT）。快速Fourier变换（FFT）被誉为二十世纪最伟大的算法之一，其探索和研究过程可以追溯到高斯。本小节中，我们将介绍一种全新的方法，从矩阵分解的角度来理解快速Fourier变换。

我们可以直接通过矩阵W和向量a相乘的形式，来计算a的离散Fourier变换 a，也就是说，矩阵W的第k行与向量a做内积，从而得到 a中的第k个元素。每次内积需要做n次乘法运算，因此，整个离散Fourier变换过程共包含n2次乘法运算。

注意观察离散Fourier变换所对应的矩阵和向量相乘的形式：(www.xing528.com)

我们可以发现其中的一些规律。比如说，我们要计算第1行和第n/2行的结果，按照矩阵和向量相乘的形式，我们总共需要进行2n次操作，也就是说，

但是，我们稍微做一下调整，就可以大大减少上面两个过程的计算量。例如，我们令：

于是，(8.71)中的两个计算过程则可以通过：

直接求得。而上面的计算方式只进行了n+2次操作，节省了将近一半的计算量。

然后，我们来计算第2行和第n/2+1行的结果，也会发现类似的规律。此时，

此时，我们可以通过：

计算第2行和第n/2+1行的结果。同样，上面的计算方式只进行了n+2次操作，节省了将近一半的计算量。继续计算下去，不难发现：

其中，

是一个单位矩阵，而矩阵

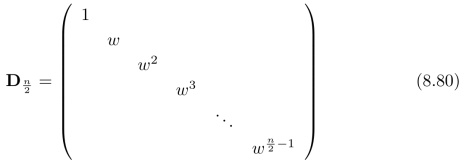
是一个对角矩阵，而矩阵：

用于获取向量a中的偶数项元素；矩阵

用于获取向量a中的奇数项元素。下面的置换矩阵

用以对向量a中的元素进行重新排列。事实上，从式(8.76)到(8.78)所给出的是：离散Fourier变换矩阵W n的矩阵分解形式，也就是说，

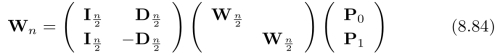
一个不包含“0”元素的矩阵W n被分解成了3个稀疏矩阵，从而使得计算量减小了一半^[4]。继续对上式中的矩阵做分解，我们可以进一步得到：

其中，

于是，在原有基础之上，又节省了一半的计算量。将上面的操作过程一直进行下去，矩阵W变得越来越稀疏，也就是说，

直到最后变为一个单位矩阵为止，如图8.4所示。

每经过一次操作，非零元素都减少为原来的一半。非零元素由最初的n2个变为（单位矩阵中的）n个，因此，操作次数为log2 n。式(8.78)中最左边矩阵中非0且非1的元素个数为n，该次操作对应值n次乘法运算；式(8.85)中最左边矩阵中非0且非1的元素个数也为n，

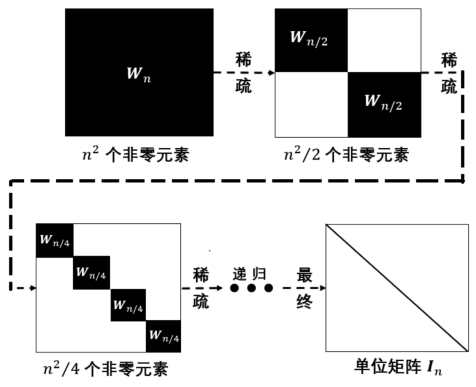
图8.4　快速Fou rier变换算法是：对离散Fou rier变换矩阵W做矩阵分解。使得矩阵变得越来越稀疏，直到最终变为一个单位矩阵为止。

该次操作也对应值n次乘法运算。继续分析下去，不难证明：对应每一次操作，都要进行n次乘法运算。因此，快速Fou rier变换中，乘法运算的总次数为n log2 n，远低于直接使用离散Fou rier变换（即：矩阵乘以向量）的乘法运算次数n2。最后，我们再次强调：

•快速Fourier变换（FFT）只是离散Fourier变换（DFT）的快速计算方法，而并非一种新的变换！

因此，快速Fou rier变换（FFT）的计算结果就是离散Fou rier变换（DFT）的结果！