离散傅里叶变换简介：理论及应用

进一步，我们想将上一小节中的分析拓展到循环卷积的情况。此时，相应的操作除了把向量“整体向下平移一个单位”外，还需要把“移出去”的元素an-1再“补回来”，作为向量a的第一个元素，也就是说，

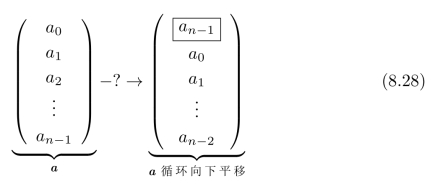
正如在上一小节中所分析的，借助于多项式，可以将向量中的元素“整体向下平移”，因此，我们先从多项式开始进行推理和分析，在分析的过程中，再逐步考虑如何对多项式施加约束，从而将“移出”向量的元素“补回去”。首先，定义多项式：

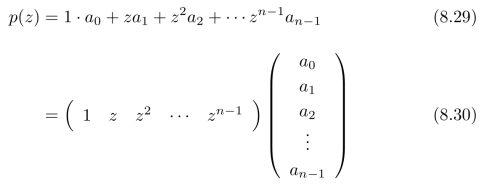
在多项式的两端同时乘以z，就得到了“整体平移一个单位”后的向量所对应的多项式，也就是说，

被移出向量的元素an-1所对应的基是zn。如果元素an-1被“补回去”作为向量的第一个元素，那么，它所对应的基是1。因此，要想将被移出向量的元素an-1被“补回去”，只需令：

此时，多项式(8.31)可以被进一步写为：

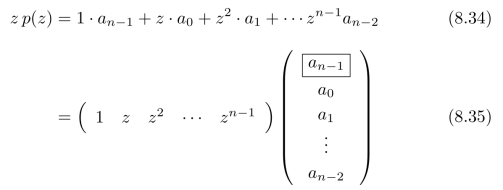
此时，z的取值不再是任意的，而是必须满足方程式(8.33)。这样的z总共有n个：这n个zk恰好构成了复平面中单位圆上的n等分点，如图8.3所示。

图8.3　为了将被移出向量的元素an-1被“补回去”，作为向量的第一个元素，需要满足条件zn=1。这样的z总共有n个，它们恰好构成了复平面中单位圆上的n等分点。

此时，基（函数）z也相应地变成了：由一组{zk}（其中k=0,1,2,···,n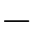1）所组成的一个n维列向量：

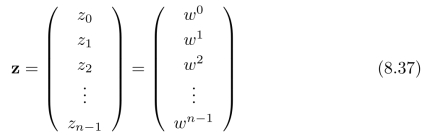
其中，

相应的，我们可以计算向量z的l次方：

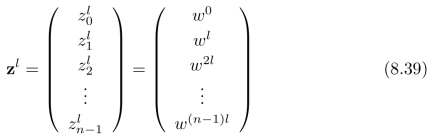
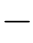此时，基（函数）zl也相应地变成了：由一组（其中k=0,1,2,···,n1）所组成的一个n维列向量z l。将这n个列向量放在一起，就构成了一组基，记为：

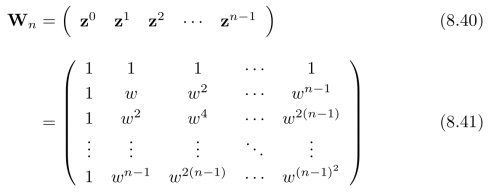(www.xing528.com)

矩阵W n又被称为离散Fou rier变换（DFT）矩阵。本质上，DFT矩阵是一组（多项式）基1,z,z2,z3,···,zn-1在约束条件(8.33)下的离散形式。矩阵W n中的列向量z0,z1,z2,···,z n-1又称为离散Fou rier变换的一组基。一个重要的结论是这组基相互之间是正交的，也就是说，

我们可以通过计算：两个向量的内积，来判断两个向量之间是否正交。对于两个复向量z k和z l，内积的定义为：

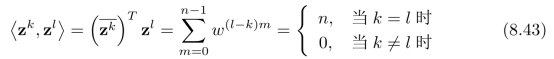
其中，z k表示向量z k的共轭，也就是说，对向量z k中的每一个元素取共轭。注意，w(l-k)m构成一个关于m的等比数列。我们可以应用等比数列求和公式（以及条件wn=1），直接得到上面的结论。

矩阵W n的Herm itian转置（也称为共轭转置）为：

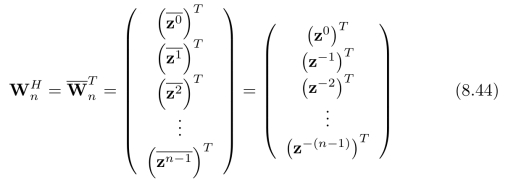
进一步，我们可以直接计算：

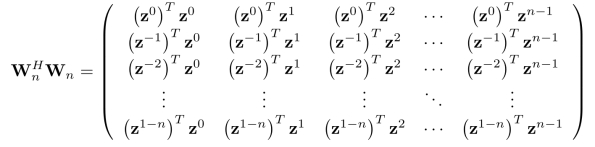
其中I n表示一个n×n的单位矩阵。于是，我们求出了矩阵W n的逆：

上式也被称为：离散Fou rier逆变换（IDFT）的矩阵。注意，根据式(8.33)，可以得到：

于是，我们可以进一步得到：

进一步，离散Fourier变换（DFT）矩阵可以被简化为：

离散Fourier逆变换（IDFT）的矩阵可以被进一步简化为：

注意，W n是一个对称矩阵，也就是说，=W n。