循环卷积计算方法及应用简述

我们还有一个问题没有解决，式(8.8)中矩阵A中的“空白”位置的元素是什么？注意，我们在整体向下平移向量a=(a1,a2,···,am)T的过程中，矩阵A中出现了没有被“触碰”到的“空白”位置（矩阵A的“右上角”）。

这些空白位置的元素应该被“设置”成什么值？一种自然的选择是将这些元素全部设置为0，如图8.1所示。当然，这并不是唯一的选择，我们还可以选择：

•将移出矩阵的元素“放回”到矩阵的相应列中的空白位置！

具体地说，将矩阵的第一列a整体向下平移，形成矩阵的第二列，移出去的元素an-1被“放回”作为第二列的第一个元素（空白位置）；然后，矩阵的第二列整体向下平移，形成矩阵第三列，移出去的元素an-2被“放回”作为第三列的第一个元素（空白位置）；以此类推进而生成矩阵A c，

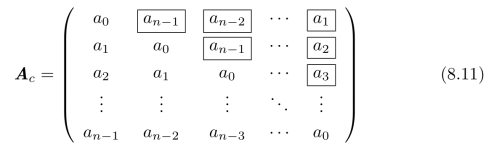
我们用“方框”标出了被“放回”的元素。此时，矩阵A c是一个方阵，也就是说，m=n。

注意：矩阵A c同时也是一个Toep litz矩阵，也就是说，矩阵A c的对角线上的元素都相同。因此，存在一种与图8.1类似的方式，来生成矩阵A c，首先，对向量a进行周期延拓，即令：

然后，通过逐一向下（整体）平移向量a c，即可生成矩阵A c，如图8.2所示。注意观察矩阵A c的代表列（第一列）a T与代表行（最后一行）b之间的关系不难发现同样的规律：

•向量b=(an-1,an-2,···,a0)是a的转置a T=(a0,a1,···,am-1)经过翻转后得到的！

所不同的是，矩阵A c并不是整体平移向量b，使得b逐步“进入”矩阵A再“走出”矩阵A而生成的。矩阵A c的生成过程为：首先对向量b进行周期延拓，生成

(www.xing528.com)

然后，整体平移向量b c，使得b c逐步“进入”（n×n的）矩阵区域再“走出”（n×n的）矩阵区域而生成的（如图8.2所示）。

由于系统A c也是由列向量（系统的单位冲击响应）a=A e1=(a0,a1,···,an-1)T生成的，因此，输出信号y可以表示为：系统的单位冲击响应a与输入信号x的作用结果，记为：

图8.2　对于循环卷积（周期卷积）。矩阵A c的各个列向量也是：矩阵A c的第一列a=(a1,a2,···,am)T逐一整体向下平移而生成的。与图8.1所示的离散卷积不同的是：移出矩阵A c的元素被“放回”到矩阵中相应列中的空白位置（用“方框”标出）。矩阵A c的第一列整体向下平移，形成第二列，移出去的元素an-1被“放回”作为第二列的第一个元素（空白位置）；然后，矩阵A c的第二列整体向下平移，形成第三列，移出去的元素an-2被“放回”作为第三列的第一个元素（空白位置）；以此类推进而生成矩阵A c中的所有列向量。矩阵A的各个行向量是：向量b=(am,am-1,···,a1)逐步“进入”矩阵A再“走出”矩阵A而生成的。矩阵A的（代表性）行向量b与列向量a之间的关系是：b是a T经过翻转后得到的。

我们称a⊗x为向量a与向量x的循环卷积（或周期卷积）。

将式(8.11)中的矩阵A c代入式(8.14)，可以得到循环卷积（或周期卷积）的具体计算形式^[2]：

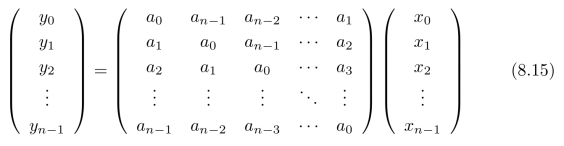
逐一计算向量y中的各个元素。事实上，周期本身就对应着模运算：

除以n的余数。观察对应元素的下标，不难发现如下规律：

其中n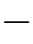1≥l,k≥0，s=0,1,2,···,n1，而mod(a,n)表示a除以n后所得到的余数。