离散信号与线性系统分析

所谓离散信号，就是一个向量，实际应用中，我们研究的是有限维向量x=(x1,x2,···,xn)T，对应的线性系统是一个矩阵：

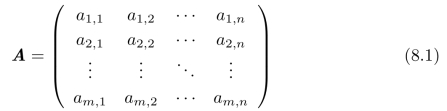
线性系统的作用是：将一个向量x=(x1,x2,···,xn)T变成另一个向量y=(y1,y2,···,ym)T，也就是说，

我们也称向量x为系统的输入信号，向量y为系统的输出信号。

8.1.1　单位冲击响应

我们的第一个问题是：如何通过观察系统的输入信号和输出信号来了解系统的特性？乍一看，这是一个难以实现的任务，因为系统的“输入/输出”信号是关于向量x和y的，而系统的特性是关于矩阵A的。解决这个问题的方法是：选取一系列“特殊”的输入信号！如果我们将输入信号选为x=e1=(1,0,0,···,0)T，那么，所得到的输出信号y=A e1=(a1,1,a2,1,···,am,1)T正好是矩阵A的第一列！然后，我们可以将输入信号选为x=e2=(0,1,0,···,0)T，那么，所得到的输出信号y=A e2=(a1,2,a2,2,···,am,2)T正好是矩阵A的第二列。同理，我们可以继续得到矩阵的第三列A e3、第四列A e4、······，直到最后一列A e n。也就是说，

•通过观察一系列特殊的输入信号e1,e2,···,e n所对应的输出信号A e1,A e2,···,A e n，我们就得到了线性系统（即：矩阵A）的全部信息！

向量e1=(1,0,0,···,0)T类比于连续信号情况下的“无限冲击函数”，对应的向量A e1=(a1,1,a2,1,···,am,1)T类比于连续信号情况下的“无限冲击响应”。我们不妨将单位向量e1的系统输出结果（即矩阵A的第一列）

称为系统的单位冲击响应，在信号与系统理论中，“无限冲击响应”相关内容的核心是：通过观察系统的“输入/输出”信号来了解系统的特性！从线性代数的观点来看，就是将矩阵的各个列向量A e1,A e2,···,A e n提取出来！

对于任意的x，向量A x是：矩阵A的各个列向量的线性组合，线性组合系数为x的各个元素，即：

注意：矩阵的各个列向量A e1,A e2,···,A e n是一组特殊的输出信号。对于任意的输入信号x，其对应的输出信号为：这组特殊的输出信号A e1,A e2,···,A e n的线性叠加，相应的叠加系数x1,x2,···,xn为输入信号x的各个元素。这个结果又被称为叠加原理。

•通过观察线性系统的“输入/输出”信号，可以了解线性系统的特性，进而可以根据（已有的）对系统“输入/输出”信号的观察结果，预测线性系统对任意输入信号的输出结果。

要了解系统的特性，我们需要一组（特殊的）输出信号A e1,A e2,···,A e n，但是，在某些特殊的情况下，我们只需要一个输出信号A e1（系统的单位冲击响应）即可。例如，

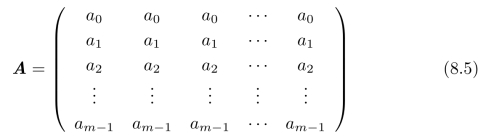
矩阵的所有列向量都相同，此时，A e1=A e2=···=A e n。这种情况过于特殊，我们将讨论一种更为一般的情况，即所谓的移不变系统。

8.1.2　移不变系统与卷积

我们将探寻一种特殊的系统，该系统可以根据系统的单位冲击响应（即：矩阵A的第一列）A e1得到（或推出）系统的全部信息。要根据矩阵A的第一列推出矩阵A的所有列，其前提条件是：

•矩阵A的各个列向量都是根据矩阵A的第一列按照某种已知的方式生成的！

除了式(8.5)所示的对矩阵A的第一列进行重复复制的情况外，一种更加一般的情况是：

•对矩阵A中的第一列进行整体平移，从而逐一地生成矩阵A中的其他列向量。(www.xing528.com)

也就是说，矩阵的第二列是矩阵的第一列整体向下平移一个位置形成的；矩阵的第三列是矩阵的第二列整体向下平移一个位置形成的；按照上述规律继续进行下去，从而（逐一地）生成矩阵中所有的列向量。此时，生成的矩阵A为：

矩阵A又被称为移不变系统，“移”是指：列向量的整体（向下）平移；“不变”是指：列向量的模式（元素a0,a1,···,am-1的排列顺序）始终保持不变。不难发现，式(8.6)中矩阵A的各个对角线上的元素都相同，这类矩阵又被称为Toep litz矩阵^[1]，是一类重要的矩阵。

式(8.2)中的输出信号y是线性系统A与输入信号x的作用结果，而线性移不变系统A又是由列向量（系统的单位冲击响应）

生成的，因此，输出信号y可以表示为：系统的单位冲击响应a与输入信号x的作用结果，记为：

我们称a*x为向量a与向量x的卷积。具体定义为：

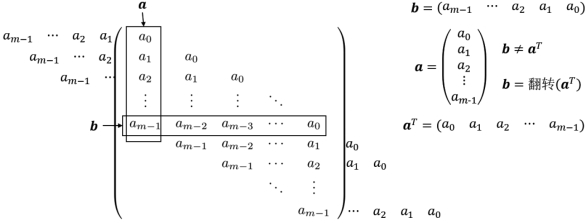
图8.1　移不变系统和离散卷积。矩阵A的各个列向量是：矩阵A的第一列a=(a0,a1,···,am-1)T逐一整体向下平移而生成的。矩阵A的各个行向量是：向量b=(am-1,am-2,···,a0)逐步“进入”矩阵A再“走出”矩阵A而生成的。矩阵A的（代表性）行向量b与列向量a之间的关系是：b是a T经过翻转后得到的。

•首先，通过（逐一地）对列向量a进行整体（向下）平移，生成一个Toep litz矩阵A；然后，通过“矩阵/向量”相乘A x，得到卷积结果a*x=A x。注意，式(8.8)只给出了卷积的定义，并没有（直接）给出卷积的计算式。向量y中的各个元素是：由矩阵A中的各行（逐一）与向量x做内积而得到的。我们前面一直在讨论矩阵A中的各个列向量，而计算卷积要用到矩阵A中的各个行向量，因此，计算卷积的核心问题是：

•如何根据矩阵A中的列向量得到矩阵A中的行向量？或者，如何根据矩阵A的第一列a得到矩阵A中的（各个）行向量？

矩阵A的（代表性）行向量b=(am-1,am-2,···,a0)并不等于矩阵A的（代表性）列向量a的转置a T=(a0,a1,···,am-1)，而是a T经过翻转后得到的结构（如图8.1所示），也就是说，

•向量b的第一个元素对应于向量a的最后一个元素，向量b的第二个元素对应于向量a的倒数第二个元素，以此类推。此外，矩阵A的各个行向量是：

•整体平移向量b，使得b逐步“进入”矩阵A再“走出”矩阵A而生成的。行标每增加1，向量b就整体向左平移一个位置。

通过上述步骤，我们根据向量a（系统的单位冲击响应）生成了矩阵A中的各个行向量，进而可以直接计算A中各个行向量与x的内积，得到卷积结果a*x中的各个元素。

最后一个问题是：卷积结果a*x中元素的个数。由式(8.8)可知：卷积结果a*x中元素的个数等于式(8.6)中矩阵A的行数。矩阵A共有n列，因此，在生成矩阵A的过程中，向量a总共被整体向下平移的了n1次，而向量a=(a0,a1,···,am-1)T中共有m个元素，因此，矩阵A的行数为m+n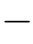1。最终，我们得到如下结论：

•一个m维向量a与一个n维向量x的卷积结果a*x的维数是m+n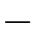1。

将式(8.6)中矩阵A代入式(8.8)，可以得到卷积的具体计算形式：

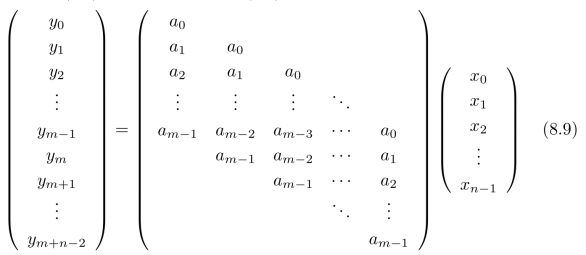
逐一计算向量y中的各个元素：y0=a0 x0，y1=a1 x0+a0 x1，y2=a2 x0+a1 x1+a0 x2，···。观察对应元素的下标，不难发现如下规律：

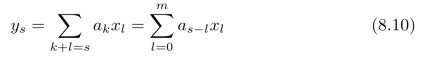
其中s≥l,k≥0，s=0,1,2,···,m+n2。