转动惯量极值的求解及简化图像生成：习题探讨

习题7.1根据图7.3中的二值图，请分别计算：区域面积、中心和朝向，从而为后续的机器臂抓取任务提供依据。

习题7.2在计算朝向的过程中，如果直接通过式(7.23)、(7.24)和(7.25)来计算a、b和c，我们需要再次进行扫描，也就是说，通过第一次扫描来算出中心，然后用于式(7.23)、(7.24)和(7.25)中所描述的第二次扫描计算。请问：是否可以只通过一次扫描，就直接计算出区域面积、中心和朝向？如果能，请给出具体方法。

提示：请证明如下关系：

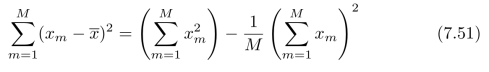
习题7.3请证明：转动惯量的极值可以被写为如下形式

其中，a、b和d的定义为：式(7.23)、(7.24)和(7.25)。证明：E≥0。请说明：什么时候E=0？

习题7.4请证明：式(7.20)中所给出的沿着倾角为θ的轴的二阶矩，可以被整理为如下的表达式

请证明：上式可以被进一步写为如下形式

上式中的ϕ等于多少？

习题7.5 a、b和d的定义分别为：式(7.23)、(7.24)和(7.25)。

(a)如果我们所使用的变量是x和y，而不是x′和y′，那么，a、b和d的表达式是什么？

(b)本章中给出了：转动惯量关于sin 2θ和cos2θ的表达式。进一步，请将其写为：关于sinθ和cosθ的表达式。

习题7.6有时候，将一个图像的形状简化为：一个只具有零阶矩、一阶矩和二阶矩的简单图形，是非常有用的。让我们来考虑一个边界为椭圆的区域。椭圆的两个半轴分别为：x轴和y轴，并且，两个半轴的长度分别为α和β。因此，椭圆的方程为：

证明：沿着某一条过原点的轴，该椭圆（区域）的二阶矩的最大值和最小值分别为：πα3β/4和παβ3/4。

假设对于某一个图像区域，在给定一条倾角为θ的轴以后，该区域的二阶矩为如下形式：

请计算：该区域的“等效椭圆”的长轴和短轴。区域的“等效椭圆”是指：该区域和它的“等效椭圆”具有相同的转动惯量。

习题7.7如果向量v具有如下性质，也就是说，存在常数λ，使得Mv=λv，那么，v被称为：矩阵M的特征向量；常数λ被称为：相应的特征值。

(a)证明：如下的2×2矩阵

有两个实的特征值：

提示：齐次线性方程组有非零解，当且仅当：它的系数矩阵的行列式等于零。

(b)证明：对应的两个特征向量分别为：

(c)证明：这两个特征向量相互垂直，并且，其模长为：

(d)最小转动惯量所对应的轴是什么？

习题7.8请说明如何通过：水平投影、竖直投影、沿着倾角θ方向的投影pθ(t)，来计算积分：

其中，沿着倾角θ方向的投影pθ(t)为：

请问：θ需要满足什么约束条件？

习题7.9本章中，我们假设：二值图是一个0/1矩阵（即：由0和1所构成矩阵）。同样，我们可能会用到：图中的一组区域边界。我们可以将每一个边界都近似地表示为一个多边形。

请证明：我们可以通过下式来计算曲面的面积。

(www.xing528.com)

式(7.63)中的积分是沿着：R的边界∂R，按逆时针方向进行的。进一步，请说明：如何通过上述结论来推导出式(7.50)。

提示：使用Green积分定理：边界上的线积分等于边界所围成的区域上的面积分。

习题7.10本题中，我们将研究：如何生成标准图形（例如：直线和圆）所对应的离散二值图。在很多实际应用中，都会涉及这个问题，例如：在第2章2.5.2小节中，我们介绍了计算机层析成像（CT）技术，其中的一个重要任务是：自动确定图2.14中的某一条直线所对应的离散点集，进而自动生成式(2.70)中的0/1矩阵A。

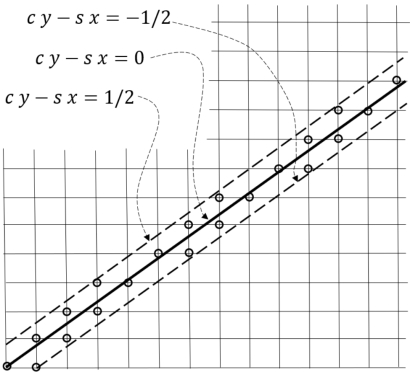
图7.20　假设直线过原点，并且，和x-轴之间的夹角θ在0°和45°之间。我们将直线的宽度设为1个像素距离，此时，直线的离散二值图就是：所有使得-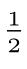≤c y-s x≤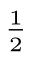成立的整数对(xn,yn)。

(a)首先，让我们来考虑一个特殊情况：直线过原点，并且，和x—轴之间的夹角θ在0°和45°之间。我们将直线的宽度设为1个像素距离，如图7.20所示。此时，我们的问题就变得清晰明确了，也就是说，寻找所有使得

成立的整数对(xn,yn)，其中c=cosθ,s=sinθ。使得式(7.64)成立的整数对都是从(x0,y0)=(0,0)开始的，我们可以通过“跟踪”（包括计算和存储两个过程）：

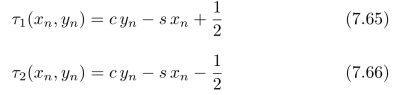
来找到所有的整数对(xn,yn)。算法的基本过程为：假设(xn,yn)

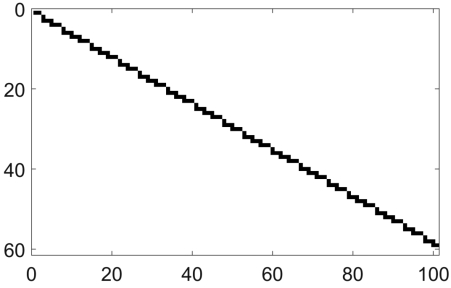
图7.21　与x-轴夹角为30°的离散直线。在二值图中，直线所对应于离散点集。

满足式(7.64)，计算

然后，执行下面的更新过程：

1.如果τ1≥0，令(xn+1,yn+1)=(xn+1,yn)；更新τ1和τ2，也就是说，τ1(xn+1,yn+1)=τ1(xn,yn)s，τ2(xn+1,yn+1)=τ2(xn,yn)s。

2.如果τ1＜0，进一步，计算

然后，继续执行下面的更新过程：

•如果τ2≤0，令(xn+1,yn+1)=(xn,yn+1)；进一步，更新τ1和τ2，也就是说，令τ1(xn+1,yn+1)=τ1(xn,yn)+c，τ2(xn+1,yn+1)=τ2(xn,yn)+c。

•如果τ2＞0，令(xn+1,yn+1)=(xn+1,yn+1)；进一步，更新τ1和τ2，也就是说，令τ1(xn+1,yn+1)=τ1(xn,yn)+cs，τ2(xn+1,yn+1)=τ2(xn,yn)+cs。

请结合图7.20说明算法的正确性。进一步，请编写程序生成一条θ=30°的离散直线，如图7.21所示。提示：可否去掉条件“和x—轴之间的夹角θ在0°和45°之间”？

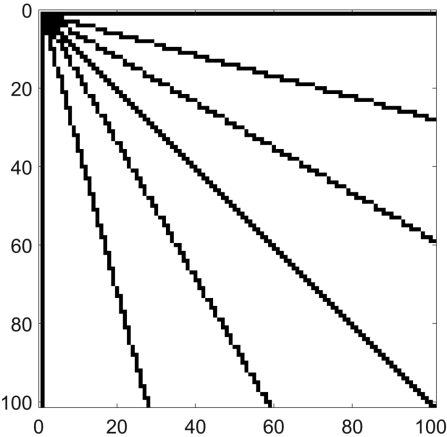
图7.22　与x-轴的夹角θ从0°到90°，间隔为15°的所有（过原点的）直线

(b)在上一小题给出的算法中，我们需要“跟踪”两个量τ1和τ2，来生成对应的直线。如果我们想要只“跟踪”一个量，例如τ1，来生成一条离散直线，应该做何调整？请用这种方法编写程序生成一条θ=30°的离散直线（图像大小为60×100）。提示：如何确保式(7.68)中的τ2始终是一个正数（或者始终是一个负数）？

(c)如果直线和x—轴之间的夹角θ在45°和90°之间，我们应该如何调整算法，生成对应的离散直线？如何将其拓展到任意角度的情况？请画出θ从0°到90°，间隔15°的所有（过原点的）直线，如图7.22所示。

(d)如果直线不经过原点，我们应该如何调整算法，生成对应的离散直线？于是，我们可以逐一地生成一组平行直线。请生成一组与x—轴之间的夹角θ=30°、线与线之间等间距（例如13个像素距离）的平行直线，如图7.23所示。

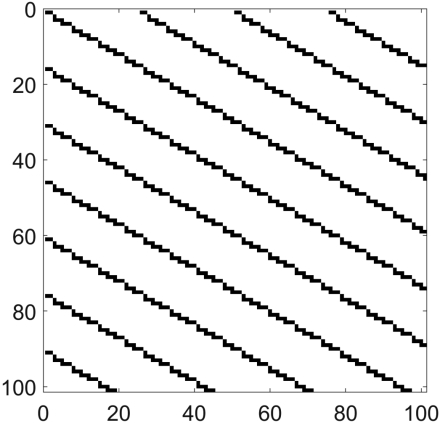
图7.23　与x-轴的夹角为30°的一组等间隔的平行直线

(e)对于每个方向，我们都可以生成一组平行直线，从而完成图2.13中的CT扫描过程。请用一张100×100的图像，例如图2.3(a)，来进行CT扫描实验，完成研究报告。

提示：在CT扫描实验的过程中，二值图7.21中的离散直线事实上就是一个索引表，用以逐个“查找”对应的像素点。

【注释】

[1]图7.4中的程序和演示视频参见：http://peop le.csail.m it.edu/wangliang。我们分别演示了如何采用深度优先算法和广度优先算法标注连通区域。

[2]零阶矩（面积）是一个数；一阶矩构成一个向量；二阶矩构成一个矩阵。

[3]我们后面会讲到，这种定义方式的一种缺陷是：求解过程需要使用迭代，无法直接计算得到解析解。

[4]注意：(c,s)T为单位长度向量，对于一般情况，首先需要进行归一化，即除以向量

[5]关于特征值和特征向量的相关内容参见：《线性代数引论》(第四版)第六章内容，Gilbert Strang[著]，王亮，张全兴，于欣妍[译]，中国青年出版社。

[6]更简洁的方法是使用特征值的性质：1)特征值之和等于矩阵的迹；2)特征值的乘积等于矩阵的行列式，也就是说，λ1+λ2=a+d和λ1λ2=ad-b2。

[7]参见：L.W ang＆B.K.P.Horn,“Machine V ision to A lert Roadside Personnel of Night Traきc Th reats,”IEEE Trans.on In telligen t Transportation System s,pp.3245-3254,2018.