如何计算物体的朝向？投影法优化方案

我们也想判断物体在视野中的放置方式，即：物体的朝向。和判断物体的面积和位置比起来，这个问题要困难一些。假设：物体沿着某个方向比较长，沿着其他方向则相对较短，那么，我们可以将物体的朝向定义为：（使得）物体“最长”的方向^[3]。

我们如何定义（使得）物体最长的方向？一个直观的方法是：计算物体在直线（或方向）上的投影，然后将使得投影最长的直线方向，选为物体的朝向。如图7.9所示。

在建立模型之前，我们需要做一些数学上的准备工作。首先，需要深入探讨如下两个子问题：

•如何描述一条直线？

•如何计算一个点在直线上的投影？在此基础上，我们可以通过计算：二值图中各个（非零）像素点在直线上的投影，从而得到整个二值图在直线上的投影。

7.4.1　投影

要确定平面上的某一条直线，需要一个定点()T和一个方向(c,s)T，其中，

上标T表示“转置”，θ为直线与x轴之间的倾斜角（如图7.10所示）。注意，向量(c,s)T的长度为1，被称为直线的方向向量，对于确定物体朝向的问题，我们将定点()T选为物体的中心。

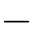向量(s,c)T是方向向量（即：直线所在的方向）(c,s)T沿逆时针方向旋转90°得到的，被称为直线的法向量。容易验证，法向量(s,c)T垂直于方向向量(c,s)T，即：(c,s)T(s,c)=0。

对于直线上任意一点(x,y)T，向量(x,y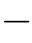)T平行于直线的方向向量(c,s)T（如图7.10所示）。因此，法向量方向(s,c)T垂直于向量(x,y)T，也就是说，(s,c)(x,y)T=0，具体形式为：

图7.9　为了定义（使得）物体最长的方向？我们需要计算物体在直线上的投影，然后将使得投影最长的直线方向作为（使得）物体最长的方向。

注意：(s,c)T(x,y)表示：向量(x,y)T在法向量(s,c)T上的投影长度。式(7.7)可以进一步整理为：

也就是说，

式(7.9)给出了直线的几何解释：

•直线上所有的点在法向量方向(s,c)T上的投影都相同，等于（直线上的某一个）固定点(,)T在法向量方向(s,c)T上的投影。也就是说，法向量方向(s,c)T上，（整条）直线被投影成了一个点。的投影(,)T。向量(xn,yn)T在直线上的投影为向量(

进一步，我们需要计算平面上一点(xn,yn)T在直线（式(7.7)）上,)T，如图7.11所示。投影向量(,)T的长度为：向量(xn,yn)T与直线方向向量(c,s)T的內积（即(c,s)(xn,yn)T）；投影向量(,)T的方向为：直线方向向量(c,s)T，于是，我们得到如下关系式：

图7.10　要确定平面上的一条直线，需要一个定点(,)T和一个方向(c,s)T=(cosθ,sinθ)T，其中，θ为直线与x轴之间的倾斜角。直线上的点(x,y)T在法向量(-s,c)T上的投影长度为定值，等于定点(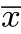,)T在法向量(-s,c)T上的投影长度。

L式可以进一步整理为：

或者简写为：

其中，

称为投影矩阵[2]，向量P u为：向量u在(c,s)T方向上的投影^[4]。注意，P是一个实对称矩阵，并且，容易验证：P 2=P，连续投影两次等价于只投影一次，因为投影的投影还是投影本身！

(c,s)T的模长，此时，P=((c,s)T(c,s))/（(c,s)(c,s)T）。

图7.11　向量(xn-,yn-)T在直线上的投影为向量(-,-)T。投影向量(-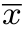,-)T的长度为：向量(xn-,yn-)T与直线方向向量(c,s)T的內积；投影向量(-,-)T的方向为：直线方向向量(c,s)T。

由式(7.11)，可以得到点(xn,yn)T在直线（式(7.7)）上的投影：

进而可以通过遍历所有的{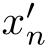}，找到最大值和最小值，于是，我们就找到了物体在直线（式(7.7)）上投影的两个端点和，进而，可以得到物体在直线上投影的长度：

最终，我们得出了计算“使得投影最长”的直线方向的算法：

1.首先，遍历θ=0,Δθ,2Δθ,3Δθ,···,π，得到物体在不同直线上的投影长度{L(θ)}:={L(0),L(Δθ),L(2Δθ),L(3Δθ),···,L(πΔθ)}；

2.然后，遍历{L(θ)}，找到使得L(θ)取得最大值的θ；最终确定对应的直线（即：式(7.7)）。

最后，需要指出的是，式(7.14)中的矩阵

图7.12　投影点=(,)T所对应的（从原点出发的）向量等于向量u1和u2的和，

即：=u1+u2。向量u1为：点p n=(xn,yn)T所对应的（从原点出发的）向量在直线方向向量(c,s)T上的投影；而向量u2为：点=(,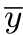)T所对应的（从原点出发的）向量在直线法向量(-s,c)T上的投影。

正好是：在法向量方向的投影矩阵！图7.12给出了式(7.14)的几何解释。投影点所对应的（从原点出发的）向量等于向量u1和u2的和，即：=u1+u2。向量u1为：点p n=(xn,yn)T所对应的（从原点出发的）向量在直线方向向量(c,s)T上的投影；而向量u2为：点所对应的（从原点出发的）向量在直线法向量(s,c)T上的投影。

上述通过计算物体在直线上的投影长度来寻找（使得）物体“最长”的方向的方法存在许多问题，例如：1)计算复杂度较高，需要进行迭代；2)只能求得近似的“最长”方向，而非精确结果。造成上述问题的原因是：计算式(7.15)中L(θ)以及最大化式(7.15)中L(θ)的过程都不存在解析解。我们希望建立一种存在解析解的模型来确定物体的朝向，以克服上述这些问题。

图7.13　图像中某一区域的朝向可以被定义为：（使得图像中的物体具有）最小转动惯量的转动轴的方向，也就是说，当一个和图像区域形状相同的“均匀薄片”物体绕着这个轴旋转时，物体的转动惯量最小。

7.4.2　转动惯量

在实际应用中，我们通常选取：使得物体产生最小二阶矩的轴，来作为物体的朝向。在二维情况下，这个轴也是：使得物体产生最小转动惯量的轴。我们首先选取一条经过物体中心的线，然后计算：物体上所有点到这条线的距离平方的和：

我们希望：我们所找到的这条线使得这个平方和取得最小值。式(7.17)中，rm表示：物体上的第m个点(xm,ym)T到直线的距离。注意，我们还没有找到这条直线，我们的优化目标是找到这条直线。

为了计算式(7.17)中E的最小值，我们首先需要计算：平面上的点p m=(xm,ym)T到直线（式(7.7)）的垂直距离rm，即：图7.14中向量的长度。注意，向量是向量在直线法向量n=(s,c)T上的投影，因此，

进一步，可以得到：

于是，物体（包含M个点）的转动惯量为：(www.xing528.com)

其中矩阵S为：

式(7.20)的具体形式为：

其中，

式(7.22)是一个二次型[2]，我们可以通过特征值分析来有效求解二次型极值问题^[5]。注意，式(7.22)中的矩阵

是一个实对称矩阵，即：S T=S，因此，矩阵S有两个相互垂直（或正交）的特征向量[2]。假设u1和u2是矩阵S的两个特征向量，对应的两个特征值为λ1和λ2，根据定义：

进一步，可以计算：

带入式(7.27)，我们发现：

图7.14　向量p m-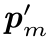 =(xm- ,ym- )T是向量p m-=(xm-,ym-)T在直线的法向量方向n=(-s,c)T上的投影，其中，是点在直线上的投影点。

如果λ1/=λ2，那么=0，也就是说，u1和u 2相互垂直（或正交）。如果λ1=λ2，那么u 1和u 2的线性组合也是矩阵S的特征向量，此时，特征向量u1和u2张成矩阵S的特征子空间，我们可以选取两个相互垂直（或正交）的向量u1和u 2作为特征子空间的基。

进一步，我们可以将两个特征向量u 1和u2归一化为单位长度的向量，此时，u 1和u 2满足如下性质：

于是，任意单位长度的向量n都可以表示成u 1和u2的线性组合：

注意，=1，带入式(7.30)，即可得到约束条件=1。于是，我们可以进一步计算式(7.20)中的转动惯量，即：

不是一般性，假设λ1≤λ2，最终，我们得到：

转动惯量E的最小值λ1对应于，此时，n=u1；而E的最大值λ2对应于，此时，n=u2。使得物体转动惯量最小的朝向所在直线的法向量n为：矩阵S的最小特征值λ1所对应的（单位长度）特征向量u1。注意，直线的方向向量(c,s)T垂直于直线的法向量n，并且，u1垂直于u2（参见式(7.30)），因此，使得物体转动惯量最小的朝向(c,s)T为：

•矩阵S的最大特征值λ2所对应的（单位长度）特征向量u2。

矩阵S是一个2×2的实对称矩阵，我们可以直接求出特征值λ1和λ2以及特征向量u1和u2的解析表达式。矩阵SλI的行列式等于0（其中矩阵I是2×2的单位矩阵），以此得到特征方程^[6]：

我们可以求得特征方程的两个根为：

令e=，可以进一步得到：

由(Sλ1 I)u1=0可得：

同理，可以进一步得到：

由(Sλ2 I)u2=0可得：

最终，我们求得了物体朝向(c,s)T的解析解：

物体朝向(c,s)T与x轴的夹角为：

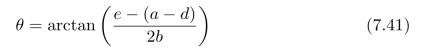
较之于上一节中的基于投影长度的物体朝向判断方法，基于转动惯量方法可以直接计算物体的朝向，不需要使用迭代算法来近似求解。

在一些智能交互任务中，物体的朝向信息是非常有用的，例如：在抓取物体的过程中，首先，根据中心(确定机械手要移动到的位置；然后，根据朝向(c,s)T调整机器手的姿态；最后，对物体进行抓取操作。再比如，对物体的智能识别。直观上，物体越“圆”，朝向信息越不明显；物体越“长”，朝向信息越明显，因此，物体的最小转动惯量λ1和最大转动惯量λ2的比值：

可以作为判断物体形态特征（即：物体有“多么圆”）的一个标准。对于直线，τ=0；对于圆，τ=1。当然，也可以采用其他的判断准则，例如：“差别”比上“均值”，具体形式为：

另外一个计算量更小的判断标准是：几何平均值与算术平均值比值的平方（参见第10章10.5小节的内容），也就是说，

这里用到了矩阵特征值的下面两个性质：

在下一节中，我们实现了一个夜间车灯识别系统，形态学指标τ被用来识别圆形的车灯。当然，区域面积也是一个重要的指标。

最后需要指出的是：矩阵S是一个半正定矩阵，也就是说，矩阵S的两个特征值λ1和λ2都是非负数。根据式(7.20)，对于任意的向量n，对应的二次型E=n T Sn都非负，因为。这正好是半正定矩阵的定义。我们也可以直接计算两个特征值λ1和λ2的正负。根据式(7.23)和式(7.25)可知：a≥0和d≥0，因此，式(7.35)中的λ2≥0。根据柯西-施瓦兹不等式，ad≥b2，进一步，可以计算：

因此，λ1≥0。矩阵S的两个特征值λ1和λ2都非负。