如何用质心表示平面物体的位置

标注出各个连通区域之后，我们可以对图像中的各个物体分别进行处理，进而分析其几何性质。本节中，我们针对二值图中的单个物体进行计算和分析。

7.3.1　区域的面积

对于给定的二值图bi,j，我们可以通过下面的公式：

来计算图像中的物体的面积，其中，m和n是二值图（一个0/1矩阵）的行数和列数。注意，区域面积A也被称作：b(x,y)的零阶矩。对于图像中有多个物体的情况，式(7.2)计算的是所有物体的总面积。

7.3.2　区域的位置

图7.8　二值图中的一个区域的位置可以被定义为：该区域的中心，也就是说，和该区域形状相同的均匀薄片物体的质心。

我们如何确定物体在图像中的位置？通常情况下，物体包含很多点，因此，我们必须给出“位置”这个术语的精确意思。在实际应用中，我们通常使用物体的区域中心来表示物体的位置，即：(www.xing528.com)

•将这个区域看作是：由某一种均匀物质所构成的平面物体，物体的质心就是该区域的中心（如图7.8所示）。

质心是一个特殊的点，如果我们将物体的全部质量集中在这一点，那么，相对于任何方向，物体的静力矩都不发生变化。在二维情况下，物体关于y轴方向的一阶矩（即：静力矩）为：

物体关于x轴方向的一阶矩（即：静力矩）为：

其中()为区域的中心，即：

在式(7.3)和(7.4)中，等号左边的积分正好等于区域面积A（参见式(7.2)）。为了计算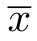和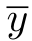，区域面积A不能为0。