如何对二值图进行标注连通区域？

首先，我们必须将图像中的各个区域分别标注出来，然后，分别计算各个区域的几何特征。计算机才能“看到”：二值图7.2(b)中包含3个区域，并将其中2个大的区域在图7.2(c)中标注出来。

7.2.1　种子算法

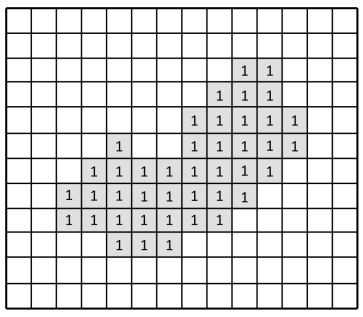
图7.3　事实上，二值图就是一个由0和1组成的二值矩阵。

种子算法是一种对二值图中“物体”进行标注的方法，通过“填充”的方式，对各个连通区域逐一进行标注，具体过程为：选取一个bij=1的点，并且，赋予这个点以及和它连接在一起的点一个标记；下一步，对所有与这些标记点相邻的点（除了那些已经被标注的点以外）进行标注；然后，不断地重复下去。当这个递归过程完成以后，这个图像区域就被标注完毕了。紧接着，我们可以继续选择一个新的起始点，然后，对下一个图像区域进行标注。为了能够找到一个新的未标记区域，我们可以使用一种“对称”的方式，来对图像进行简单扫描。一旦发现还没有被标注的bij=1的点，我们就以该点作为新的起始点，然后进行标注。如果在对所有图像单元进行扫描以后，还没有发现这样的点，那么，我们就完成了对二值图像中所有“物体”的标注，如图7.4所示^[1]。需要注意的是，背景可能会被分割为多个连通区域；并且，物体中也可能有“洞”。我们可以用类似的方法对背景（以及物体中的“洞”）进行标注，也就是说，我们将关注于bij=0的点，而不是bij=1的点。

为了实现种子算法，我们首先要定义连通性，以确定近邻点。假设我们使用正方形作为基本单元来对图像进行剖分，那么，在这种情况下，我们可以粗略地将近邻点“认为是”：和给定图像单元（即：像素点）的四条边相连接的四个图像单元。但是，我们应该如何看待：和给定像素点的四个角相连的四个像素点呢？因此，对近邻点的定义存在如下两种可能的情况：

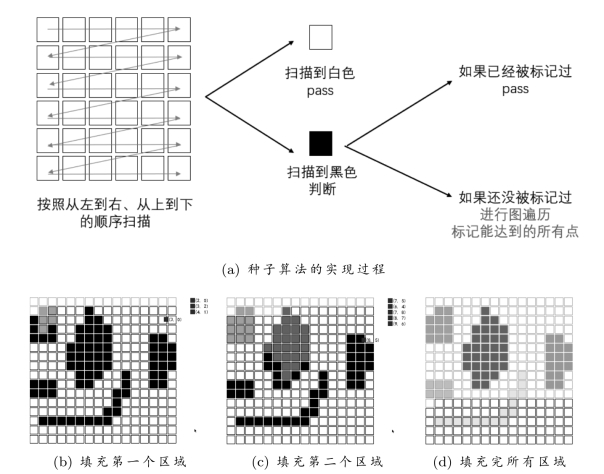
图7.4　种子算法对二值图进行扫描，同时，通过“填充”的方式，对各个连通区域逐一进行标注。要实现种子算法，首先需要定义像素点之间的连通性，进而确定近邻点。

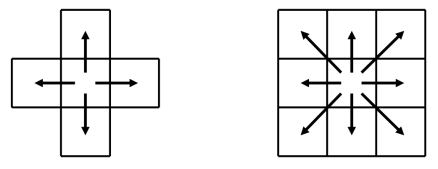
这两种不同的定义方式分别为：

•4—连接：只有和给定图像单元（即：像素点）的（4条）边相连的（4个）像素点，才被认为是（给定像素点）的近邻点。

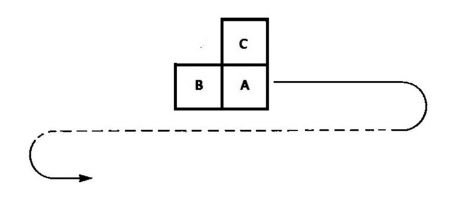
图7.5　在一次常规的光栅扫描中，我们让模式窗口在图像中划动，再根据：模式窗口所对应的像素点上的标注值，来对相应的像素点进行标注。

•8—连接：和给定图像单元的（4个）角相连的（4个）像素点，也被认为是（给定像素点）的近邻点。

7.2.2　串行标注算法

现在，我们要介绍一种标注算法，这种标注算法更适于对图像进行串行扫描，并且，它不需要使用递归操作。我们约定：1)对图像进行逐行扫描，并且，行的编号顺序是从上到下的；2)对于每一行，我们按照从左到右的顺序，对该行中的像素点进行扫描（如图7.5所示）。如果我们采用4—连接，那么，B点正上方的像素点D也是和A相连的，因此，我们还需要考虑D的标注结果。根据我们事先约定的扫描顺序，当我们扫描到某一个像素点A时，A点左边的像素点B已经被标注过了，并且，A点正上方的像素点C也被标注过了。想一想，如果我们采用8—连接，应该如何修改图7.5？

为了简化问题，我们只对图像中的物体进行标注。具体过程如下（如图7.6所示）：

1.如果A是0，那么，我们不需要进行任何操作。

2.如果A是1，并且，点B或者点C也被标注了，那么，我们同样也需要将B或者C的标签复制给A。

3.如果点B和C都没有被标注，并且，A是1，那么，我们必须选取一个新的标签，来对A进行标注。这表示：从A点开始，我们对一个新的物体进行标注。

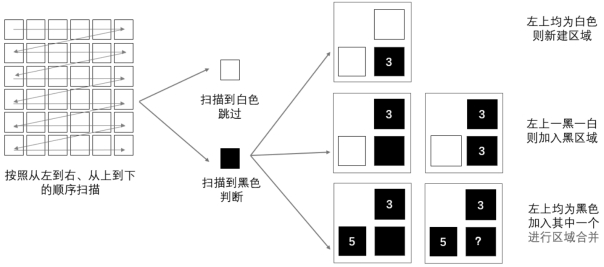
图7.6　在串行标注过程中，我们可能会碰到这样的情况：前面认为是相互分离的两个区域，实际上是连接在一起的。我们必须记录下：这两个标签实际上是等价的，进而进行区域合并。

4.还有一种可能性是：B和C都被标注了。如果B和C的标签是相同的，那么，这并不会产生任何问题；但是，在我们关于4—连接的约定中，B和C是不相邻的，因此，B和C的标签有可能不同。对于这种情况，我们会将两个不同的标签赋予同一个物体（如图7.6所示）。这意味着图像中的两个区域通过A点连接在了一起。此时，我们必须在A点做上新的“记号”，用来表示：A点上的这两个标签（即：B和C的标签）是等价的；然后，我们任意选取其中一个标签，来对A进行标注。

对于串行标注算法，我们无法避开的问题是：一个连通区域可能被标注了多个标签，这是串行标注算法必须付出的“代价”。串行扫描结束后，我们需要将图像中具有等价标签的各个区域合并在一起。

如果我们想要让图像中的各个区域都具有唯一的标签，那么，我们需要对串行扫描结果进行二次扫描，从而将同一个具有代表性的标签赋予：具有等价标签的多个区域。我们可以从该区域所拥有的多个等价标签中，随机选取出的一个标签，来作为该等价区域的标签。(www.xing528.com)

串行扫描结束后，所有标签构成一个“图”，我们将其称为标签图，包括：结点（即：区域的标签）和边（即：连通的两个区域）。区域合并就是：

•根据标签图中结点和边的信息生成（各个子图的）最小张成树（即：连通区域所包含的所有标签）。在图7.7的例子中，串行扫描结束后，标签图中的结点为：V={1,2,3,4,5,6,7,8}，边为：E={{2,3},{2,4},{3,5},{6,7},{7,8}}，最小张成树结构为：T={{1},{2,3,4,5},{6,7,8}}。根据V和E生成T的基本算法如下所示：

1.初始化：生成一个空链表T，作为最小张成树链表。

2.循环：如果V非空，执行下面的操作

•选取V中的第一个元素vi；

•以vi为根节点生成一个最小张成树Ti，将生成的最小张成树“合入”最小张成树链表：T={T,Ti}。

•在V中删除Ti中包含的所有结点；在E中删除所有包含Ti中结点的边。

对于图7.7的例子，首先选取结点1作为根节点，遍历E以后，发现没有和结点1相连的边，因此，第一个最小张成树就是结点1。

此时，T={{1}}，E={{2,3},{2,4},{3,5},{6,7},{7,8}}，V={2,3,4,5,6,7}；然后，以结点2作为根节点，遍历E以后，得到第二个最小张成树T2={2,3,4,5}，此时，V={6,7,8}，E={{6,7},{7,8}}，T={{1},{2,3,4,5}}；最后，以结点6作为根节点，遍历E以后，得到新的最小张成树T3={6,7,8}，此时，V为空集，循环结束，最终得到的最小张成树结构为：T={{1},{2,3,4,5},{6,7,8}}。

可以使用深度优先算法或广度优先算法进行图遍历，进而得到最小张成树。例如，采用广度优先算法，具体过程为：

1.初始化：生成一个链表Ti={vj}，其中vj为V的第一个元素。令n=0，m=1。

2.循环：令n=n+1，如果n≤m，执行下面的操作：

•选取Ti中的第n个元素vk，遍历E，如果发现某一条边

{vk,vl}包含vk，执行下面的操作：

(a)将vl加入Ti，即：Ti={Ti,vl}；

(b)在E中删除边{vk,vl}，在V中删除结点vl；

(c)令m=m+1；

•继续遍历E，直至完成对所有边的搜索。

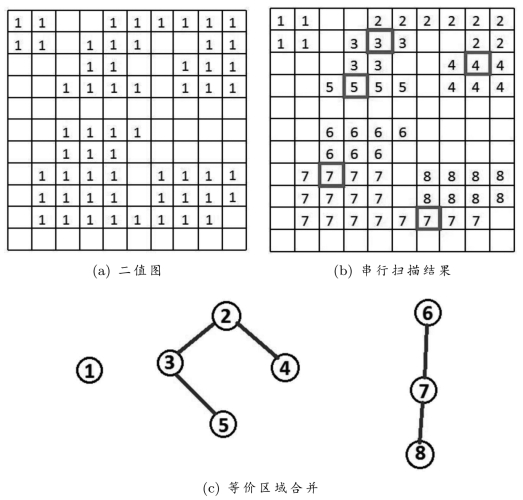
图7.7　串行扫描过程所生成的“图结构”，包括：结点V={1,2,3,4,5,6,7,8}和边E={{2,3},{2,4},{3,5},{6,7},{7,8}}。区域合并就是：根据图中结点和边的信息生成（各个子图的）最小张成树结构T={{1},{2,3,4,5},{6,7,8}}。

•在V中删除vk。

3.在V中删除最小张成树的根节点vj。

在图7.7所示的例子中，以结点2作为根节点，此时，V={2,3,4,5,6,7,8}，E={{2,3},{2,4},{3,5},{6,7},{7,8}}，初始时，T2={2}，遍历E的过程中，发现边{2,3}包含结点2，于是将结点3放入T2（此时T2={2,3}），删除边{2,3}和结点3；继续遍历，发现边{2,4}包含结点2，于是将结点4放入T2（此时T2={2,3,4}），删除边{2,4}和结点4；剩下的边中不包含结点2，（第一次）遍历完成，此时，V={2,5,6,7,8}，E={{3,5},{6,7},{7,8}}。于是，重新开始遍历E，寻找包含结点3的边，发现边{3,5}包含结点3，于是将结点5放入T2（此时T2={2,3,4,5}），删除边{3,5}和结点5；剩下的边中不包含结点3，遍历完成，此时，V={2,6,7,8}，E={{6,7},{7,8}}。继续开始重新遍历E，寻找包含结点4的边，由于E中没有包含4的边，继续新的遍历，寻找包含结点5的边，E中也没有包含5的边，结束循环，最终，得到最小张成树T2={2,3,4,5}。最后，在V中删除根节点2，此时，V={6,7,8}，E={{6,7},{7,8}}。

后面我们将会提到：如果我们的目的是计算区域的零阶矩、一阶矩以及二阶矩的总量，那么，我们甚至可以绕过区域合并这一步，而只需要简单地将等价标签所对应的各个（等价）区域的零阶矩、一阶矩、二阶矩的计算结果分别对应地加在一起即可。通常，图像是一行一行地进行扫描的。当每一个像素点(i,j)被读进来以后，我们首先判断bij的值，如果bij=1，那么，我们在前面已经计算的累积量中，分别对应地加上1、i、j、i2、ij和j2。这些量的总和分别近似等于：面积、一阶矩和二阶矩^[2]。扫描结束以后，通过这些量，我们可以非常容易地计算出：区域的面积、位置和朝向。