辐射源有释放能量,并不意味着这些能量就能够被感受(或测量)到。我们能够测量到这些能量(进而形成图像)的前提条件是:辐射能量能够穿过空气到达相应的传感器。事实上,地球上的大气层会吸收大部分的辐射能量,但是,存在两个大气透过窗口(实验观测结果):中波红外(3~5微米)和长波红外(8~12微米),这使得红外成像成为可能。作为一个应用实例,图4.7中给出了对夜空中飞机的红外成像结果。
总结起来,红外成像的基本原理包括如下两个方面的内容:
1.理论成果:理想辐射源的总辐射能量E(T)与绝对温度T的四次方成正比[5],
![]()
对于黑体,比例系数为 σ=σ≈5.67×10-8 Wm-2K-4,对于灰体,比例系数为
σ=σ≈5.67×10-8 Wm-2K-4,对于灰体,比例系数为 σ=α×σ,其中吸收率α<1。
σ=α×σ,其中吸收率α<1。

图4.8 红外图像非常模糊,而且图像中的物体区域没有清晰的边缘。可见光图像被用以配合红外图像,更好地提取人脸区域,从而提升温度测量精度。
2.实验成果:地球的大气层中存在两个辐射透过窗口:中波红外(3~5微米)和长波红外(8~12微米),使得部分辐射能量能够穿过大气到达红外图像传感器。
疫情让我们对红外成像变得更加熟悉,机场、高铁站、食堂、办公大楼的门口随处可见红外成像仪器,用以测量过往人员的体温。如果你仔细观察,不难发现:较之于可见光图像,红外图像非常模糊,而且图像中的物体区域没有清晰的边缘,参见图4.8。可见光图像被用以配合红外图像,更好地提取人脸区域,从而提升温度测量精度。
我们将尝试从红外成像的基本原理出发,来解释这个问题。一个高温物体,它的热量会向周围扩散,从而使得周围的温度不断升高。假设物体放置在均匀介质中,于是,我们可以用如下的热扩散方程
![]()
来描述物体的温度变化过程[6]。物体不断发热,温度恒定,可以作为第一个边界条件;距离物体较远处,温度几乎不受高温物体的影响,可以近似认为温度是恒定的,作为第二个边界条件。于是,我们可以求解出式(4.25)中的T(x,y;t),进而得到理论上的红外成像结果。我们通过一个具体的例子来加深我们的理解,在下面的模型中:

数字“0”和“1”为边界条件,始终保持不变,“?”的值随时间不断发生变化。相应地,热扩散方程(4.25)被离散为如下迭代格式[7]:
![]()
其中,
![]()
表示与点(i,j)相邻的四个点的平均温度。于是,我们一下子就看清楚了热扩散方程(4.25)的物理意义:
•如果某一点的温度低于周围的平均温度,那么这一点的温度就会升高;否则,这一点的温度就会降低。
进一步,我们可以将式(4.26)整理为:
![]()
熟悉数值分析的朋友可能会马上意识到:式(4.28)是一个插值过程,当0≤τ≤1时,式(4.28)属于内插形式,因此,迭代过程是稳定的。
图4.9中给出了τ=0.3时的实验仿真结果。一开始的时候,所有的“?”都设为“0”,此时,物体的边缘是清晰的,参见图4.9(a)。随后,物体边缘的温度分布迅速变得“模糊”(参见图4.9(b));很快,扩散达到平衡,温度分布不再随时间发生明显变化(对比图4.9(c)和图4.9(d)中的结果)。(https://www.xing528.com)

图4.9 实验结果(其中τ=0.3)。(a)初始时刻,物体边缘温度差别很明显;(b)随后,物体边缘的温度分布迅速开始“模糊”;(c)很快,扩散达到平衡状态;(d)温度分布不
再随时间发生明显变化。
根据斯蒂芬-玻尔兹曼方程,我们可以计算出:图4.9(d)中的(热平衡状态时的)温度分布所对应的(归一化的)辐射能量分布,如图4.10(a)所示。由于辐射能量与绝对温度的四次方成正比,较之于温度分布,辐射能量分布中的对比度得到了增强。由于大气吸收、物理模型的偏差等因素的影响,在实际情况中,辐射能量可能达不到与绝对温度的四次方成正比,图4.10(b)中给出了辐射能量与绝对温度的平方成正比的情况,辐射能量分布变得更加“模糊”。

图4.10 热平衡状态时的温度分布所对应的(归一化的)辐射能量分布。(a)理想情况下,辐射能量与绝对温度的四次方成正比,较之于温度分布,辐射能量分布中的对比度得到了增强。(b)由于大气吸收等原因,辐射能量可能达不到与绝对温度的四次方成正比,辐射能量分布会变得更加“模糊”。
我们可以进一步完善上面的算例,边界条件“0”所在的位置应该远离物体(即:边界条件“1”所在的位置)。我们将矩阵的尺寸扩大到120×171,两个物体的尺寸仍然都设为2×2,如图4.11(a)所示。图4.11(b)中给出了平衡状态时的温度分布(经过50000次迭代后的结果),我们已经较难辨识出图4.11(b)中的两个物体。对于理想情况,我们可以根据斯蒂芬-玻尔兹曼方程计算出:图4.11(b)中的温度分布所对应的(归一化的)辐射能量分布,如图4.11(c)所示。较之于图4.10(a),图4.11(c)中的“模糊”现象更加明显(参见4.11(e))。考虑到大气吸收、物理模型的偏差等因素的影响,在实际情况中,辐射能量可能达不到与绝对温度的四次方成正比,图4.11(d)中给出了辐射能量与绝对温度的平方成正比的情况,这更加符合我们实际观测的结果。为了便于观察,图4.11(e)和图4.11(f)中分别给出了对图4.11(c)和图4.11(d)中“中心区域”的局部放大结果。
我们继续对这个算例做一些调整,让“右边”区域的温度稍微低于“左边”区域的温度,也就是说,将右边的2×2区域中的值由“1”调整为“0.8”,如图4.12(a)所示。图4.12(b)中给出了平衡状态时的温度分布(经过50000次迭代后的结果),我们很难辨识出图4.12(b)中“右边”的物体。对于理想情况,我们可以根据斯蒂芬-玻尔兹曼方程计算出:图4.12(b)中的温度分布所对应的(归一化的)辐射能量分布,如图4.12(c)所示。较之于图4.11(c),图4.12(c)中的结果会被错误地识别为“只有一个物体”(对比图4.11(e)和图4.12(e))。考虑到大气吸收、物理模型的偏差等因素的影响,在实际情况中,辐射能量可能达不到与绝对温度的四次方成正比,图4.12(d)中给出了辐射能量与绝对温度的平方成正比的情况,这更加符合我们实际观测的结果。为了便于观察,图4.12(e)和图4.12(f)中分别给出了对图4.12(c)和图4.12(d)中“中心区域”的局部放大结果。

图4.11 实验结果(其中τ=0.3)。(a)初始时刻,物体边缘温度差别很明显;(b)物体边缘的温度分布迅速开始“模糊”;(c)根据斯蒂芬-玻尔兹曼方程计算出的(归一化的)辐射能量分布;(d)由于大气吸收等原因,辐射能量达不到与绝对温度的四次方成正比,辐射能量分布会变得更加“模糊”。(e)和(f)分别为(c)和(d)的局部放大结果。
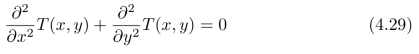

图4.12 实验结果(其中τ=0.3)。(a)初始时刻,物体边缘温度差别很明显;(b)物体边缘的温度分布迅速开始“模糊”;(c)根据斯蒂芬-玻尔兹曼方程计算出的(归一化的)辐射能量分布;(d)由于大气吸收等原因,辐射能量达不到与绝对温度的四次方成正比,辐射能量分布会变得更加“模糊”。(e)和(f)分别为(c)和(d)的局部放大结果。

图4.13 通过数值计算给出的辐射强度E(T)与绝对温度T之间的近似关系。
当然,我们也可以直接求解Lap lace方程来计算稳定状态时的温度分布T(x,y),此时,每一点的温度都等于它周围点温度的平均值。对比热扩散方程(4.25),不难发现两者之间的关系:热扩散方程在时间t=∞时的解T(x,y;∞),就是Lap lace方程(4.29)的解T(x,y),也就是说,热扩散方程(4.25)给出了:求解Lap lace方程(4.29)的一种方法。在习题4.8和4.9中,我们尝试直接求解Lap lace方程,并且,对上面的算例进行了扩展研究和探索。
当然,我们也可以通过数值计算的方式,来分析(在考虑大气吸收作用时)辐射强度E(T)与绝对温度T之间的关系,如图4.13所示。我们采用最简单的“方波”形状的滤波器,

来描述大气对光谱辐射强度R(λ,T)的吸收。首先,将式(4.12)中的R(λ,T)换成η(λ)R(λ,T),然后,通过数值积分得到图4.13中的结果。在习题4.8和4.9中,我们将进一步模拟:大气吸收对红外成像结果的影响。此外,从图4.13中可以看出:当温度低于1000 K时,我们可以近似认为:辐射强度仍然与温度的四次方成正比。
注意,图4.10、4.11和4.12中的辐射强度分布并不是红外成像系统的最终成像结果,只是理论上的“理想清晰图像”。在生成红外图像的过程中,我们还需要考虑:由成像系统自身的缺陷所引起的图像模糊和噪声,以及图像传感器的量子效率。因此,实际得到的红外图像会变得更加模糊,并且带有大量噪声,参见图4.7。在第6章和第9章中,我们会详细介绍相关内容。通过这个算例,我们了解到:
•由于存在热扩散,辐射强度并不是一个“边界分明”的特征,
因此,不管成像系统是否存在缺陷,红外图像都会存在模糊!
这将大大增加视觉感知任务的难度。正如我们在第一章中所谈到的,“感”的过程是生成图像;“知”的过程是分析图像以获取描述信息。对于红外图像,一个有趣的描述信息是:什么样的物体轮廓才能“最好”地匹配红外图像中的对应区域。不同于可见光图像,即使是对于人,也很难直接在红外图像中“精确地”看出边缘轮廓[8],特别是对于图4.12中的情况。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




