习题3.1我们用p和q来表示：入射角θi和出射角θe的余弦值。我们必须同时知道余弦值和正弦值。请证明：
习题3.2让我们来考虑一些关于图像和场景亮度的明显“悖论”。
(a)物体所成的像的辐照强度，为什么与透镜到物体表面的距离无关？毕竟，当透镜和物体之间的距离变为原来的两倍时，透镜所收集到的、从物体表面某一小块发出的光，只有原来的1/4。
(b)证明：物体表面在一个“理想”的镜面中所成的像的辐射强度，始终等于物体表面的辐射强度，而与镜子的形状无关。
(c)术语光强经常被误用。强度是指：光源在单位立体角内所发射出的功率（单位：W·sr-1——瓦特每立体角）。证明：点光源经过凸面镜所成的虚像的强度，比点光源的强度小。虚像的强度和凸面镜的曲率之间存在着什么关系？
(d)在(b)和(c)中似乎存在着明显的矛盾，请设法进行“调和”。
习题3.3考虑一个倾斜的Lam bert表面上方的半球面“天空”（如图3.12所示）。假设：Lambert表面的法向量和半球面“天空”的顶点之间夹角为α＜π/2。Lambert表面上方的半球面并不是闭合的，通过本章中关于Lambert表面的分析结果，我们知道：Lambert表面所产生的辐射强度等于E/2。剩下的半个球面是“黑暗”区域。只有和“天空”的顶点方向夹角小于θ′的那部分Lambert表面才是可见的。
(a)通过考虑相应的球面三角形，请证明：
通过上式，我们可以进一步整理得到：
提示：参见附录A.1中关于球面三角几何的有用公式。
(b)半球中的“明亮”区域对于Lam bert表面的辐射强度的贡献为：
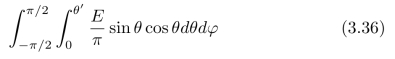
证明：上式可以被进一步写为：
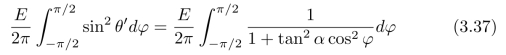
提示：
θcosθdθ=(1/2)sin2θ。
(c)根据积分公式：
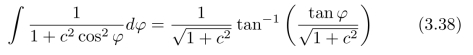
我们可以进一步求解：积分式(3.37)，其结果为(E/2)cosα。由此，我们可以算出总的辐射强度，其结果为：
习题3.4 Minnaert表面的双向反射分布函数为：
其中，0≤k＜1。对于一个准确定位的、方向为(θs,φs)的单点光源，我们令点光源的辐射强度为：
那么，物体表面所受到的辐照强度为E0。请证明：如果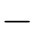
π/2≤θi≤π/2，那么，物体表面的辐射强度为：
当k取何值时，辐射强度和观测方向无关？
习题3.5证明：对于具有Lam bert反射性质的物体表面，物体表面所成的图像在区域R中的平均亮度等于：曲面的平均法向量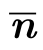
与光源方向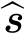
s的内积。这里，
(www.xing528.com)
其中A是指：图像区域的面积。
提示：注意，通常情况下，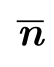
并不是一个单位向量。
习题3.6让我们来模拟物体表面的微结构。我们假设：物体表面“起伏波动”的尺度，远远超出了仪器的分辨能力。同时假设：在尺度足够小的情况下，物体表面的“起伏”使得物体表面成为：一个Lam bert反射表面。请问，在较大的尺度下（即：无法对物体表面的“起伏”形状进行分辨的情况下），物体表面是否还是一个Lam bert反射表面？分别考虑两种极限情况，即：入射光线和观测方向分别“贴近”曲面的切平面的情况。
习题3.7对于Lambert表面的情况，请证明：1)外加的连续光源可以被等效地换作一个点光源，并且，2)要确定点光源的亮度和位置，我们只需要沿着：（所有）入射光方向所形成的单位球，对连续光源的亮度进行积分，也就是说，
图3.16 我们可以在Gauss球上来进行研究。(a)对于单点光源照射Lam bert表面的情况，亮度等值线为球面上的一个圆。(b)这使得我们很容易证明：在这种情况下，对于由两个点光源所产生的光度立体视觉问题，最多存在两个解。
其中，E(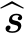
s)是指：光源沿着
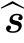s方向的辐射强度。
我们可以将这个想法用于：连续光源为上半球面的例子。这里的α是指：物体表面“小块”与竖直方向之间的夹角。参见图3.12。请证明：等效点光源的方向和“天空顶部”的方向之间的夹角为α/2；并且，其亮度和cos(α/2)成正比。提示：从物体表面小块看过去，连续光源中的有些部分是看不见的。
习题3.8理想Lam bert表面在单点光源照射的情况下，其图像辐照强度为cosθi，我们可以将其写为：两个单位向量的内积，即：
其中，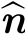
n是曲面的单位法向量；而
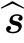s是指向点光源的单位方向向量。我们使用两个不同的点光源方向
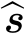s1和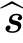
s2，分别得到两个亮度测量结果E1和E2。请求出：两个可能的曲面法向量方向。在什么情况下，曲面的单位法向量有唯一解？提示：在图3.16的基础上，进一步开展理论分析。
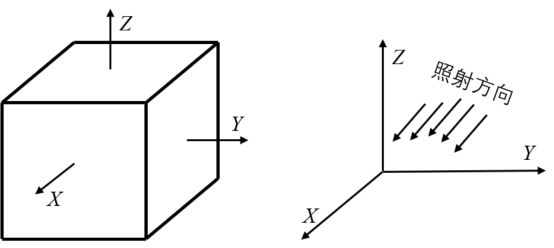
图3.17 通过计算机仿真来模拟：点光源照射立方体物体所成的图像。假设立方体的表面为理想Lam b ert表面，图像的亮度模式依赖于光的照射方向。
习题3.9本题中，我们将完成对图3.14所示的光度立体视觉技术的实验和仿真。
(a)通过计算机模拟的方式，对三个不同方向的点光源照射球面的情况进行仿真，得到三张球面亮度图像。
(b)通过动画演示的方式，移动球的位置（或等价地移动三个点光源的照射方向），对三张球面亮度图像的变化进行计算机仿真。
(c)根据式(3.32)，通过三张球面亮度的图像来估计球面的法向量分布，分析估计结果是否符合真实结果。
(d)进行实物实验，在一块黑布上放置一个球，用灯光从不同方向照射球体，得到三张球面亮度的图像，然后，根据式(3.32)来估计球面的法向量分布。根据实验结果完成研究报告。
习题3.10假设图3.17中的立方体物体的表面为理想Lam bert表面，点光源的极角方向为θ、方位角方向为φ。
(a)请计算立方体的三个可见表面的（归一化）亮度。计算出的“亮度”是辐射强度还是辐照强度？
(b)三个表面的边缘是否一直清晰可见？请给出详细解释，并对各种不同的情况做详细的分析。
(c)图3.17中的立方体物体对应于一张图像，假设其形式为：请问：a、b和c分别等于多少？图中的“?”对应于立方体物体的边缘所对应的像素点，我们可以将其取值设为：相邻区域亮度的平均值，请确定图中各个“?”的值。最终，我们得到了对立方体物体成像过程的计算模拟结果。
(d)进一步，让我们来进行仿真实验：首先，选取多个不同的光源方向(θn,φn)T，从而得到多张图像；然后，根据所得到的多张图像，估计出图3.17中立方体物体各个面的朝向。请根据实验结果完成研究报告。
【注释】
[1]关于光晕的内容，请参见第2章的内容以及图2.9。
[2]一个更加直观的理解是：(90°-θ)和φ分别对应于维度和经度。
[3]参见：Horn,B.K.P.＆K.Ikeuchi(1984)“The Mechanical Manipu lation of Random ly O riented Parts,”Scien tific Am erican,Vol.251,No.2,pp.100-111,August.
[4]我们可以通过：设定三个光源的照射方向，来进一步简化求解过程。最佳的选择是让这三个光源的照射方向相互垂直，此时，（S-1）T=S。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
