物体表面反射特性分析与优化技巧

除了光源分布以外，物体表面的反射性质也是决定成像结果的重要因素，参见图3.10。一种最常见的漫反射模型是：理想Lam bert表面（参见图3.10(a)），它具有如下两个性质：

•从各个方向进行观测，物体表面的亮度都一样；

•物体表面对入射光进行完全反射（即：吸收率为0）。

从上述定义中，我们可以推导出：理想Lambert表面的双向反射分布函数是一个常数。为了确定这个常数，我们对物体表面的辐射强度沿着各个方向进行积分，所得到的物体表面的总的辐射强度，应该等于物体表面所接收到的总的辐照强度，也就是说，

等式两边约去E cosθi，然后对φe做积分，可以得到：

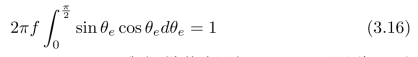
利用恒等式：2sinθe cosθe=sin 2θe。我们最终得到：πf=1。因此，对于理想Lambert表面，其双向反射分布函数为：

注意：由于理想Lambert表面的双向反射分布函数是常数，我们可以通过曲面的辐照强度，来计算出曲面的辐射强度，即：

当然，对于具有其他反射性质的物体表面，这个简单方法并不适用。

关于物体表面反射性质的另一个极端是：理想镜面反射，如图3.10(b)所示。理想镜面反射将所有沿着(θi,φi)方向的入射光，沿着(θi,φi+π)方向射出（如图3.11所示）。理想镜面反射的双向反射分布函数与δ(θeθi)δ(φeφi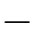π)（即两个单位无限冲积函数的乘积）成正比，但是，比例系数k是多少？我们再一次使用：在前面计算理想Lambert表面的双向反射分布函数时，所使用的方法。首先，对物体表面的辐射强度沿各个方向进行积分，从而得到物体表面的总辐射强度；然后，令物体表面的总辐射强度等于物体表面所接收到的总的辐照强度。于是，

(www.xing528.com)

根据单位无限冲击函数的定义，我们可以得到：

于是，我们可以得到理想镜面的双向反射分布函数：

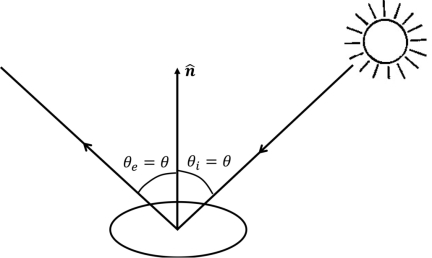
图3.11　镜面反射将：沿着某一个方向的入射光，全部反射到：由入射光方向和曲面法向量所确定的平面中，并且，由反射光线和曲面法向量所确定的反射角，等于：由入射光线和曲面法向量所确定的入射角。

进一步，我们可以计算出：对于连续光源，镜面的辐射强度。根据式(3.14)，我们可以求得：

再次地，根据单位无限冲击函数的定义，我们可以得到：

对于镜面，沿着(θe,φe)方向的辐射强度正好等于：（连续光源所射出的光线中）沿着“与(θe,φe)对称的方向”射入镜面的那部分辐射强度。这和我们的实际观测结果极其一致，因为，我们通过镜面所看见的是：连续光源的虚像！对于具有其他反射性质的曲面，这种简单关系是不适用的。

我们可以通过实验的方式，来得到双向反射分布函数。用一个放置在角度计上的灯来照射：由某种特定材料做成的、表面平坦的样本，然后，用放置在另外一个角度计上的传感器来测量辐照强度。角度计有两个旋转轴，因此，安放在角度计上的仪器可以精确地对准任意一个给定方向。用实验方法来确定双向反射分布函数非常烦琐，因为它涉及四个变量。幸运的是，通常情况下，我们只需要处理三个变量θi、θe和(φeφi)即可。

另外一个获得双向反射分布函数的方法是：建立物体表面对入射光的反射模型，然后，通过数学分析或数值模拟的方法，找到对应的物体表面反射特性。这种方法被用于：一些简单的物体表面微结构的模型。如果使用近似逼近方法，通常还有可能得到模型的解析解。我们这里不再对其做深入讨论。