双向反射分布函数简介

是什么决定场景的辐射强度？场景的辐射强度依赖于：1)“落在”物体表面的光的强弱，2)物体表面对入射光的反射率，3)光反射过程中的一些几何关系。当我们观察镜子对光的反射时，很容易理解这一点。通常情况下，物体表面的辐射强度同时依赖于：1)物体被观测的方向，以及，2)物体被照射的方向。

图3.7　我们可以用：由极角θ和方位角φ所确定的局部坐标系，来表示：入射光线和出射光线的方向。

我们可以用：“安放”在曲面上的局部坐标系，来描述这两个方向，如图3.7所示。通过(1)曲面的法向量 n和(2)曲面上的任意一条参考线，我们可以用两个角θ和φ来表示：射入或射出该曲面的光线的方向。θ表示：该方向和曲面法向量之间的夹角；而φ表示：该方向在曲面上的投影与我们所选的参考线之间的夹角。这两个角θ和φ分别称为极角和方位角^[2]。于是，我们可以将入射光的方向表示为(θi,φi)，而将射向观测者的光的方向表示为(θe,φe)，如图3.8所示。

我们可以定义双向反射分布函数f(θi,φi,θe,φe)。双向反射分布函数告诉我们：

•当光从某一个方向射入物体表面时，我们从另一个方向对其进行观测，物体表面的亮度是多少。

如果沿着入射方向(θi,φi)射入物体表面的光的强度（辐照强度）为δE(θi,φi)，而从物体表面沿着方向(θe,φe)射出的光的强度（辐射强度）为δI(θe,φe)，那么，双向反射分布函数可以被表示为：辐射强度和辐照强度的比值，也就是说，

(www.xing528.com)

图3.8　当物体表面的某一“小块”受到：沿着(θi,φi)方向的光的照射时，沿着方向(θe,φe)看过去，该小块的辐射强度与（该小块所受到的）辐照强度之间的比值，被称为双向反射分布函数。

后面，我们将研究几种理想曲面的双向反射分布函数。直接使用一个四元函数来研究：图像辐照强度和物体表面形状之间的关系，显得有点笨拙。幸运的是，对于许多物体的微表面，如果让该微表面绕着其法线旋转，那么，该微表面的辐射强度不会发生变化。在这种情况下，双向反射分布函数只依赖于：入射光和出射光之间的方位角之差φeφi，而并不单独依赖于φe和φi。这对于漫反射表面和镜面都是成立的，但是，这并不适用于某些具有特殊朝向性质的微表面，例如：一种被称为“虎眼”的矿物，一些具有特殊光泽的鸟类羽毛。

双向反射分布函数的形式必须满足一个有趣的约束条件。如果两个表面处于热平衡状态，那么，从一个表面辐射到另一个表面的辐射量，必须和：从另一个表面沿着相反方向辐射过来的辐射量保持平衡，否则，接收到较多辐射量的表面将会被加热，而另一个表面将会被冷却，因此，热平衡将会被打破。这违背了热力学第二定律。容易证明，上面这个结论意味着：双向反射分布函数必须满足Helm holtz相互性条件，即：

也就是说，双向反射分布函数具有对称性。

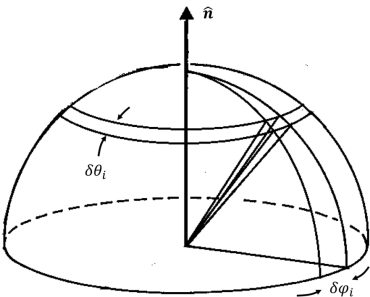
图3.9　对于连续光源的情况，我们必须在所有的入射方向上，对双向反射分布函数与光源的辐射强度的乘积求积分。