透视投影成像验证及探索—光学几何学习习题

习题12.1在分析平动和转动分量的过程中，我们得到了一些公式。本题中，我们将使用这些公式，来对第12章中所得到的一些结果进行扩展。在第12章中，我们讨论了：光流。请证明下面三个结论，即：

(a)当我们用相机“观测”一个平面物体的表面时，如果相机沿着：平行于像平面的方向运动，那么，对于所得到的光流，其Lap lace算子的处理结果为零。注意：该平面物体并不一定要平行于像平面。

(b)我们用相机“观测”一个平面物体的表面，并且，假设平面物体平行于像平面。如果相机只做平动，而不发生转动，那么，对于所得到的光流，其Lap lace算子的处理结果为零。注意：相机平动的方向并不一定要平行于像平面。

(c)如果相机绕着（除了光轴以外的）其他的轴转动，那么，对于所得到的光流，其Lap lace算子的处理结果不为零。

习题12.2对于（纯粹）转动的情况，光流场中的向量与物体和透镜之间的距离无关。向量的长度和方向取决于：转动轴和角速度。我们将转动中心定义为：光流场中速度为零的点。在某种程度上，这和我们在（纯粹）平动的问题中所定义的膨胀中心很相似。证明：在（纯粹）转动的情况下，我们可以通过：像平面上的两个点的光流，来确定：相机的运动方向。并且，请进一步说明：对于这两个点中的一个点，我们只需要知道其光流方向即可（而不需要知道其光流的大小）。请解释：为什么这并不是利用光流信息的最好方法？

习题12.3无源导航的另外一种方法需要用到：“特征”的识别和追踪。请设计和探索一些特征识别和追踪的方法，用来从物体上选取少数的特征点。当我们在视频中相邻的两张图上找到这些点之间的对应关系以后，我们就可以确定物体的运动情况。

提示：这并不是一个简单的问题。

习题12.4证明：如果f(k r)=f(r)，那么∇f(r)·r=0。其中∇表示梯度算子。梯度是一个向量，其分量为：函数f关于x和y的偏导数。

习题12.5假设：g(t)=t T Gt，并且，t为单位向量。请证明：g(t)的最优解对应于矩阵G的特征向量。

习题12.6如果我们只考虑（纯粹）平动的情况。请证明：最小化Lzu,v范数所得到的方程，和最小化Lαβ范数所得到的方程相同。请解释其原因。

习题12.7考虑纯粹平动的情况。假设我选择最小化LZ范数：

这里，远处的点的光流，将获得更大的权重。证明：这种情况下，所得到的结果只和光流的方向有关，而与光流的大小无关。

习题12.8证明：对于纯粹转动的情况，如果像平面的长为2W、宽为2H，那么，在式(12.82)中，

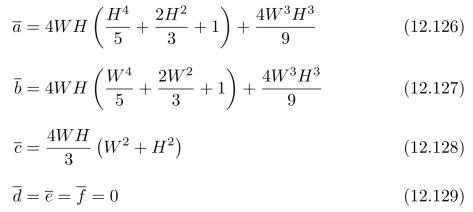
其中，的定义参见式(12.83)～(12.91)。证明：式(12.82)中的系数矩阵M是非奇异的（即：M是一个可逆矩阵）。

习题12.9对于一些极端的情况，无源导航的解可能不唯一。这里，我们将探索：被成像的物体是一个平面的情况。

(a)假设被成像的物体是一个平面，其表达式为：

其中，(X,Y,Z)T表示：曲面上某一点的坐标。证明：

其中，(x,y)T是对应的像平面上的点的坐标。

(b)证明：在这种情况下，相机运动所生成的运动场为：下面给出的关于x和y的二次多项式，即：

如果我们令：U′=U/Z0、V′=V/Z0、W′=W/Z0，那么，我们可以对式(12.132)和(12.133)做进一步化简。

(c)现在想象：有两个不同的平面物体，当相机（以两组不同的运动参数）做着两种不同的运动时，这两个平面物体所产生的光流是相同的。我们用下标来表示：两组不同的平面参数，以及，两组不同的运动参数。我们用(u1,v1)和(u2,v2)来表示两组光流。于是，“两组光流相同”具体是指：u1=u2并且v1=v2。请根据式(12.132)和(12.133)推导出：要产生相同的光流，平面参数和运动参数所需满足的8个条件：

习题12.10到目前为止，我们始终假设：无源导航的计算过程包括两个步骤：首先，估计光流；然后，通过光流信息来确定物体的形状和运动速度。这种方法非常直观，但是，也有一些缺点。本题中，我们将对其做进一步探索。本章所导出的最小二乘方法，对于图像中每一点的光流信息，都“平等地”赋予权重。但是，我们知道，图像中的某些区域比另一些区域更“可靠”。例如，对于图中亮度梯度比较小的区域，我们可以赋予其较小的系数。此外，一种更加合理的方法是：直接从时变图像中复原出物体的形状和运动信息。也就是说，我们不计算光流，而是通过光流约束方程直接推导出误差项：

上式依赖于下面两组参数，即：1)曲面的形状Z(x,y)，以及，2)运动参数(A,B,C)T和(U,V,W)T。（参见：u和v的表达式(12.9)和(12.11)）。当然，要“局部”地复原出所有的参数，只使用式(12.142)来作为约束条件是不够的。我们还需要去“度量”：（估计出的）曲面是否光滑；例如，我们可以使用

来作为：曲面“不光滑程度”的判断标准。

(a)我们令函数d(x,y)=1/Z(x,y)。请推导出：关于d(x,y)的Eu ler方程，该Euler方程是通过最小化es+λec而得到的。提示：记住：除了d(x,y)以外，“误差”总能量es+λec同时还依赖于：刚体运动的6个参数。

(b)请探索：使用式(12.143)来作为“平滑项”的基本原理，也就是说，为什么式(12.143)使用的是1/Z，而不是Z？为什么使用Lap lace算子处理结果的平方，而不直接使用两个一阶偏导数的平方和？

习题12.11请根据图11.7中的两张图像来计算碰撞时间（TTC）和膨胀中心（FOE）。在此基础上，请根据图11.7对计算结果做深入分析。进一步，请根据如下两张图像来计算TTC和FOE。

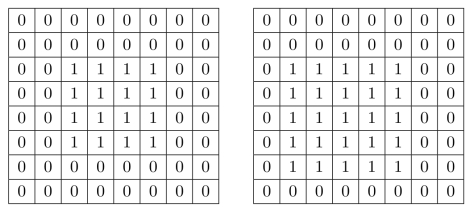
在此基础上，请使用第11章11.3小节中介绍的“稀疏光流法”来计算光流（选用4×4的窗口），然后，根据光流估计结果来对（求解出的）TTC和FOE进行深入分析，完成实验报告。

习题12.12本题中，我们来计算一个具体的例子。假设景深Z为常数，相机平动所对应的速度场为：(www.xing528.com)

其中i=0,1,2,···,m,j=0,1,2,···,n。我们想要根据光流场{(ui,j,vi,j)T}，来确定相机的相对平动速度( U, V, W)T。

图12.8　对于飞行器运动的情况，所得到的光流应该是图12.2(d)、图12.2(e)和图12.2(c)的线性组合。相应的无源导航问题就是：确定相应的线性组合系数(˜A,˜B,˜W)T。

(a)首先，我们定义速度场和光流场之间的“误差能量”：

我们通过最小化误差能量，来进行求解，也就是说，

请给出上面模型的具体表达式。

(b)请根据极值必要条件：偏导数等于零，建立起关于最优估计结果的约束方程组。

(c)通过求解(b)问中的方程组，得出最优估计结果。

提示：为了便于推导，可以令：

习题12.13本题中，我们将通过几个具体例子，来深入理解无源导航技术。我们将借助于计算机仿真实验，来完成分析和研究。

(a)为了便于理解，我们考虑一个极其特殊的情况：场景是一个竖直的平面，也就是说，景深Z(x,y)=Z0是一个常数。请设计仿真系统，系统能够根据输入的运动参数(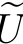 U, V, W)T生成对应的光流图像（例如图12.3(a)和图12.3(b)），然后，根据生成的光流图像，反过来估计运动参数( U, V, W)T。

(b)光流估计过程中可能含有大量的噪声。对于图12.3(c)和图12.3(d)中给出的（带有噪声的）光流估计结果，如何进一步推测运动参数( U, V, W)T？请设计算法是实现程序，进一步完善(a)中设计的计算机仿真系统。

(c)对于飞行器运动的情况，所得到的光流应该是图12.2(d)、图12.2(e)和图12.2(c)的线性组合。飞行参数控制问题就是：如何设定相应的线性组合系数( A, B, W)T，从而使得（图像中的）目标所在区域的中心点附近的光流近似为零？请设计算法是实现程序，进一步完善计算机仿真系统。

最终，请设根据实验仿真的结果，完成研究报告。

习题12.14本题中，我们探索一个应用问题：使用无源导航技术来引导无人机穿门^[6]，如图12.9所示。

(a)请根据无人机拍摄的视频计算光流。

(b)请根据无人机的飞行模式，建立相应的无源导航模型，并且，给出详细的分析说明。

(c)进一步，请建立理论模型，进而分析如何根据光流确定出膨胀中心（即：碰撞点）？

(d)请根据（前面章节中学习过的）边缘检测和角点检测的相关内容，建立理论模型和相应的检测算法，在图像中识别出门框，进而确定门框的中心点。

(e)在什么情况下碰撞点位于图像的中心？请给出具体的理论分析，为后续的控制算法设计提供理论依据。

(f)请根据：图像中门框中心点的位置，来调整无人机的姿态，从而使得门框的中心点始终位于图像中心附近。

提示：可以根据图12.2来设计姿态调整方法。

图12.9　使用无源导航技术来引导无人机穿门。

(g)最终，请设计一个系统仿真程序，能够根据无人拍摄的视频，通过虚拟仿真的形式，完成对上述功能效果的动画展示。

请设计基本算法，进行实验仿真，完成研究报告。

【注释】

[1]我们首先定义一个特征函数，对于1/Z不连续的点，特征函数的值为1；对于其他的点，特征函数值为0。然后，我们对特征函数进行积分，积分结果等于零。

[2]这是由于g(U,V,W)≥0，因此，根据式(12.63)，对于任意t，都有t T Gt≥0，这正好是半正定矩阵的定义。

[3]参见：N.Shahriar＆B.K.P.Horn.“D irect passive navigation.”IEEE Transactions on Pattern Analysis and Machine In telligence,vol.1(1987):168-176.

[4]参见：B.K.P.Horn,Y.Fang＆I.Masaki,”T im e to Contact Relative to a P lanar Surface,”IEEE Transactions on In telligen t Transportation System s,June 2007.

[5]参见：L.W ang＆B.K.P.Horn,”T im e-to-Contact control:im p roving safety and reliability of autonom ous vehicles”,In ternational Journal of Bio-Inspired Com putation,Vol.16,No.2,pp.68-78,2020.

[6]中山大学航空航天学院朱波教授提供了这一应用场景。