拓展成像模式的方法与实践

我们如何能够指望：仅仅通过一张二维图像，就能恢复出三维场景的信息？即便是使用多张图像，我们所获取的信息量似乎也不够。但是，生物系统却能够使用视觉信息和周围世界进行智能交互。此外，我们还可以通过层析成像技术，来探索物体内部的结构。

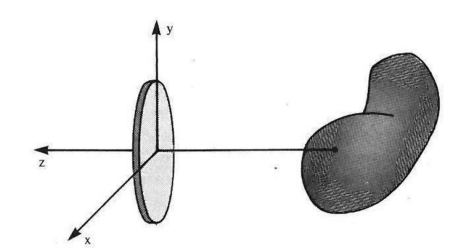
图2.12　描述曲面形状的一种简便方法是：使用曲面上的点到参考平面的垂直距离z(x,y)。通常，我们让参考平面平行于像平面。

2.5.1　物体表面：透视成像

我们所处的视觉世界有其自身的特性：我们处在均匀透明的介质之中，而我们所看见的物体却是不透明的。在我们所处的环境中，光线不会被折射或者被吸收。我们可以“跟踪”：从图像上的点出发、并且经过透镜的光线，直到它“穿过”某一个物体的表面为止。图像上某一点的亮度只依赖于：该点所对应的物体表面上的一个小区域的亮度。物体表面是一个二维流形，因此，物体表面的形状可以被表示为：图像坐标x′和y′的函数z(x′,y′)，即：图像上的点(x′,y′)T所对应的曲面上的点(x,y)到像平面的距离z(x,y)，参见图2.12。

上述前提假设并不总是绝对成立的。远处的大山似乎在颜色和对比度上发生了变化，而在沙漠中，我们可能会看见海市蜃楼。基于上述前提假设所得出的图像分析结果，在这个假设条件不成立时，可能会发生错误。因此，我们不难想象：在这种情况下，对于和环境之间的智能交互，生物视觉和机器视觉系统将会产生误导。事实上，我们可以用这种方法来解释一些光学幻象。但是，这并不表示：我们应该抛弃这些附加的约束条件，因为如果没有这些约束条件，我们将无法求解：从图像中恢复出三维“世界”的信息的问题。

事实上，我们通常所处的视觉世界是很特别的。想象我们处在一个由胶状物质所构成的世界里面，并且，在这些胶状物质中，放有一些不同颜色的颜料块，这些颜料在胶状物质中逐渐扩散开来。我们不可能通过：从某一个方向得到的观察结果，来复原出这些颜料在三维空间中的分布，因为我们没有获得足够的信息！类似的，除非碰巧遇到：不同材料之间有“尖锐”对比度的情况（例如：骨骼和软组织），否则，对于复原物体内部结构信息的问题，单张X射线图像是没有用的。对于一般情况，我们需要进行极其大量的观测，并尝试采用层析成像的方法来进行复原。因此，我们不具有超人所拥有的X射线视觉能力，或许是一件好事。

总的来说，我们会将我们的注意力集中在：那些通过常见的光学成像方式所生成的图像。我们会尽量避免去考虑：那些环境中存在大量透明（或者，半透明）物质的情况，例如，那些放大倍数很高的显微镜图像。类似地，很大尺寸的图像往往会显示出：大气对光线的吸收和折射效应。有意思的是，通过其他方式所产生出的图像，有时确实和我们所熟知的图像非常相似。这些例子包括：1)电子扫描显微镜，2)合成孔径雷达。对于这两种图像，我们很容易对其进行解释，因此，我们有希望用本书中的方法来对这两类图像进行分析。

鉴于曲面的重要性，我们可能会希望：我们能够设计出一个机器视觉系统，使得该系统可以从给定的一张或几张图像中，恢复出曲面的形状。事实上，这方面的努力已经取得了一些成果，例如：通过分析图像的明暗（即：图像亮度模式的空间变化）来恢复出物体的表面形状。相应的技术被称为光度立体视觉，在第3章3.8小节中，我们还将对其进行深入探讨（参见图3.14）。

对成像过程的深刻理解，使得我们可以从图像中恢复出关于场景的量化信息；而计算出的曲面形状可以被用于：目标识别、环境监测、路径规划等具体的应用任务。

2.5.2　物体内部：层析成像

需要指出的是：成像的方式是多种多样的，并不仅仅限于前面介绍的透视投影。如果假设我们所处环境是：由不同密度的吸光材料所填充的空间，那么，这将是一个完全不同的情况。此时，我们所想要确定的是：吸光材料的密度分布ρ(x,y,z)，它是一个关于坐标x、y和z的函数。对于恢复曲面信息的问题，一张或多张图像提供了充足的约束条件；但是，对于恢复三维空间中的信息来说，一张或多张图像所提供的约束条件却是不够的。

理论上，要解决层析成像问题，需要无穷多张图像。所谓层析成像，就是指：确定吸收材料的密度分布。图2.13给出了层析成像的物理实现过程。顾名思义，所谓“层析”，就是对物体进行“切片”。通过对每一个“切片”进行成像，再将所有“切片”的图像“拼接”在一起，最终得到物体的三维内部结构图像。具体地说，首先，确定物体上z=z0处的“薄片”的密度分布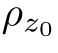(x,y)=ρ(x,y,z0)；然后，将所有的“薄片”在z轴上按照z0的顺序“拼接起来”，最终得到“薄片”的密度分布图ρ(x,y,z)。

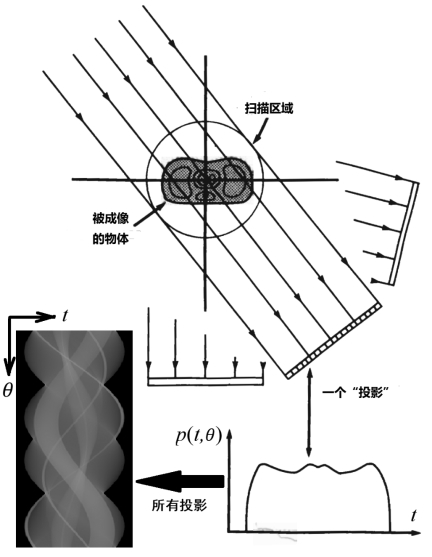
图2.13　层析成像的主题是：通过测量射线的衰减来复原出一个物体内部的吸收率密度（即：单位体积的吸收率）。沿着一组平行线x cos(θ)+y sin(θ)+t=0，可以得到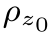(x,y)的一个（一维）“投影”p(t,θ)，层析成像算法根据生成的一组投影（即：0≤θ＜π）复原出“薄片”的吸收率密度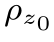(x,y)。

“薄片”内部的吸收率密度（即：单位面积的吸收率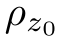）(x,y)是通过测量X射线的衰减来复原出的。如图2.13所示，沿着一组平行线x cos(θ)+y sin(θ)+t=0，可以得到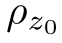(x,y)的一个（一维）投影p(t,θ)，层析成像算法根据生成的一组投影（即：0≤θ＜π）复原出“薄片”的吸收率密度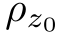(x,y)。

物理上，一束X射线沿着直线l(t,θ):x cos(θ)+y sin(θ)+t=0穿过物体，发射端的射线能量为E0，接收端的收到射线能量为El，薄片内部位于（直线l(t,θ)上的）点(x,y)处的射线能量为E(x,y)，相应的X射线能量吸收率为ρ(x,y)，则有：

方程(2.63)可以进一步整理为：

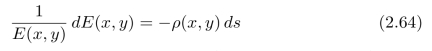
沿着直线l(t,θ):x cos(θ)+y sin(θ)+t=0对上式进行积分，可以得到：

几何上，式(2.65)中等号右侧的积分结果：

是吸收率ρ(x,y)沿着直线l(t,θ):x cos(θ)+y sin(θ)+t=0的投影。图2.13所示的是ρ(x,y)沿着一个方向的投影，选取不同的θ，可以得到ρ(x,y)沿着各个方向的投影，参见图7.9。总结：

•层析成像（CT）通过物理手段（X光透射衰减）得到物体“薄片”内部吸收率ρ(x,y)的投影：p(t,θ)=ln E0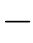ln El。

图2.13中层析成像所得到的“图像”为：物体“薄片”内部吸收率ρ(x,y)沿着各个方向的投影（由投影曲线拼接而成的曲面），而不是吸收率ρ(x,y)本身。因此，层析成像是“所见非所得”的，这一点与前面介绍的透视投影成像是不同的。我们需要使用反演算法^[12]，根据投影p(t,θ)推算出吸收率ρ(x,y)。注意，式(2.65)离散后得到一个线性方程组，求解该线性方程组，即可求得吸收率ρ(x,y)的离散近似形式，该方法又称为代数重建法（先离散，再求解）。对于学习过信号与系统相关课程的读者朋友，应该会意识到：式(2.65)是一个线性系统，而求解ρ(x,y)是一个滤波过程^[13]！因此，可以通过设计滤波器来计算ρ(x,y)，该方法又称为滤波逆投影法（先求解，再离散）。(www.xing528.com)

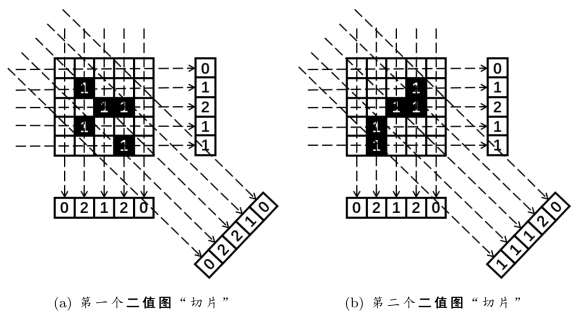
图2.14　只通过部分投影无法确定具体的结构信息。(a)和(b)的结构信息完全不同，但是它们的水平投影和竖直投影却完全相同。随着投影数目的增加（例如斜45°投影），不同的结构信息就逐步地被识别和测量出来了。

图2.14所示的简化情况可以帮助我们更好地理解反演成像。投影是一个对“切片”内部结构信息的测量过程。随着投影数量的增加，越来越多的测量结果被获取到。我们希望依据获取到的测量结果，反演出“切片”内部结构信息。需要指出的是，只通过部分投影无法确定出“切片”内部的结构信息。例如：图2.14(a)和2.14(b)的结构信息不同，但是它们的水平投影和竖直投影却完全相同。随着投影数目的增加，不同的结构信息就逐步地被识别和测量出来了，例如：图2.14(a)和2.14(b)的结构信息在斜45°方向上的投影存在明显差别。

图2.14中，未知数总共有25个，记为x=(x1,x2,···,x25)T（例如按照逐行扫描的方式进行编号），每一条“带箭头的虚线”对应于一个方程，所有（共15个）方程构成了一个线性方程组[2]：

其中，投影结果b是已知数据，可以通过X射线扫描的物理方式被测量出来，参见式(2.65)。对于图2.14(a)，

对于图2.14(b)，

矩阵A中的元素是0或1，A中的每一行对应于一条“带箭头的虚线”。“虚线”经过的像素点所对应的A中的元素为1；“虚线”不经过的像素点所对应的A中的元素为0。对于图2.14，相应的矩阵为：

在第7章的习题7.10中，我们将探索如何自动生成矩阵A。目前，我们还无法求解式(2.67)，因为方程的个数小于未知数的个数。随着扫描方向的不断增加，当方程的个数大于未知数的个数时，通过求解式(2.67)，我们就可以反演出“切片”内部的结构信息。这就是著名的代数重建法，我们将通过习题2.8进一步开展深入研究。

我们也可以直接求解式(2.66)中的吸收密度ρ(x,y)。首先，对式(2.66)中所有过点(x0,y0)T（沿着直线l0(t,θ):x0 cos(θ)+y0 sin(θ)+t=0）的投影p(t,θ)=p(x0 cos(θ)+y0 sin(θ),θ)做积分，可以得到

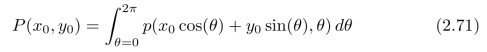
式(2.71)中，θ的积分区间取为0到2π，而不是0到π，是出于CT机械结构设计的考量。如果将θ的积分区间取为0到π，那么，每做一次CT扫描，滑环只转半圈，在下次扫描时，还需要再转回来。在实现上，让滑环转一整圈会更加便捷！代入式(2.66)，可以进一步得到：

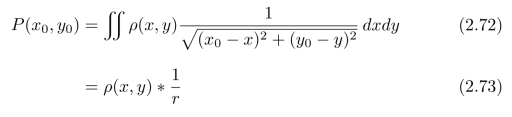
图2.15　对木质材料进行无损检测。层析成像检测技术能够连续穿透竹材，通过透照成像与断层成像获取其结构与全面的密度特征。(a)对竹材“切片”进行X射线扫描而得到的投影结果p(t,θ)；(b)通过代数重建法得出的关于吸收密度ρ(x,y)的反演结果。

其中“*”表示二维卷积[6]，式(2.72)是根据“微面积”之间的关系：得出的。

最终，我们得到了求解ρ(x,y)的方法，称为滤波逆投影法。该算法分为两步，1)逆投影：直接计算式(2.71)得到函数P(x0,y0)；2)滤波：求解式(2.73)得到ρ(x,y)。在第9章中，我们会详细讨论如何求解卷积系统(2.73)。

在中国科学院高能物理研究所王哲研究员所主持的一项研究课题中，应用层析成像技术来对木质材料进行无损检测，如图2.15所示。竹材具有生产周期短、经济价值高、易实现可持续经营等显著特征，属于一类非常重要的非木材产品，在我国森林资源不足的情况下，充分科学合理开发利用竹类资源，具有重要的意义。木材和竹材的结构检测既是研究其生长特征的重要内容，也是指导其科学合理加工，促进其利用率提高的重要手段，而竹材是一种变异多孔性、不均匀性的各向异性材料，这给研究竹材物理力学性质带来了难度。利用X射线层析成像技术可以很好地解决这个问题。

图2.16　我们可以将所有的二维断层图（包括图2.15(b)）按照“切片”顺序排列起来，形成一个三维立体图。进而，可以看到从竹材表皮到内部的维管束分布规律。

X射线能够连续穿透竹材，通过层析成像检测技术（即：透照成像与断层成像），我们无需复杂的制样过程，就可以获取到关于竹材的结构信息与密度特征。图2.15(a)是：对截面宽度为15mm×15mm的竹材“切片”进行X射线扫描而得到的投影结果p(t,θ)；图2.15(b)是：通过代数重建法得出的关于吸收密度ρ(x,y)的反演结果。

进一步，我们可以将所有的二维断层图（包括图2.15(b)）按照“切片”顺序排列起来，形成一个三维立体图，如图2.16所示。从图2.16中，我们可以看到（从竹材表皮到内部的）维管束分布的变化规律。利用X射线层析成像技术，我们获取到了竹材微观结构，包括：竹材节间维管束、薄壁组织的三维结构信息，以及竹节维管束的空间分布。在此基础上，我们可以建立竹材密度分布的数学模型，并利用模型预测和测试竹材密度，得出竹材密度变化规律，进而对树木生长规律等课题开展深入研究。

事实上，计算机层析成像（CT）技术的第一个应用并不是医学诊断（尽管这项技术在1979年获得了诺贝尔医学奖）。Berthold K.P.Horn教授曾经和我谈到过：他的老师A.Cormack教授在建立了计算机层析成像的理论模型后（1963年），并没有马上得到实际应用。最初是瑞士的一家公司想尝试通过计算机层析成像技术来探测雪山里面的空洞，进而预测雪崩。位于雪山两侧的两架直升飞机分别携带X射线的发射和探测装置，用以实现X射线扫描。由于工程实施上的困难，例如：两架直升机之间的协同、使用放射性物质的法律约束等，雪山空洞探测最终没有得到广泛应用。直到1972年，G.Hounsf ield将CT技术用于医学成像，才使得这项技术迅速进入到大众的视野。

最后，我们再次强调：成像是对场景的测量过程，图像是对应的场景测量结果。成像的方式可以是多种多样的，例如：（与人眼结构类似的）透视投影、（所见非所得的）层析成像等。