透镜：如何利用透镜获得足够的光强？

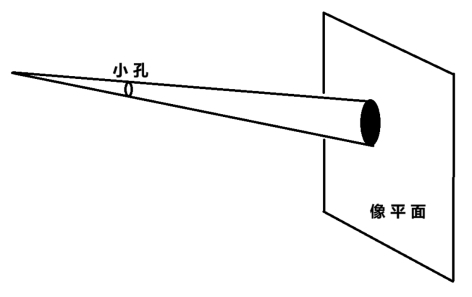
图2.8　为了使像平面上的感光区域获得足够的光强，小孔必须有一定的面积。此时，透视投影模型不再成立。空间中的点透过小孔会在像平面上形成一个“光斑”，所形成的图像是这些光斑的叠加结果。正因如此，小孔成像实验得到的是一张模糊的图像。

事实上，上面介绍的透视投影是一个理论模型。要在像平面上得到一定强度的光照，相机的光圈必须有一定的尺寸。因此，我们前面介绍的小孔的直径就不能为零。于是，我们前面关于投影的简单分析（即：小孔成像模型）将不再适用，因为，当小孔的直径不为零时，场景中的一个点所成的像将会是一个小光斑，而不再是一个点（如图2.8所示）。此时，生成的图像是这些光斑叠加的结果。正因如此，小孔成像实验得到的图像往往是模糊的^[9]。

我们不能将小孔做得太小的另外一个原因是由于光的波动性。在小孔的边缘上，光将发生衍射，因此，这些光将在像平面上“散播”。当小孔变得越来越小时，入射光的“散播”范围将变得越来越大，因此，入射光中越来越多的能量将会被“散播”到：偏离入射光方向的“地方”。

为了解决小孔相机的上述问题，我们现在考虑：在成像系统中使用透镜（如图2.9所示）。一个理想的透镜具有如下两个性质：1)它的投影方式和小孔模型相同，同时，2)将一定数量的光线汇聚在一起。透镜越大，从物体处看过去，对应的立体角也越大，相应的，透镜所截取的从物体表面反射（或发出）的光也会越多。通过透镜中心的光线不会发生偏转，在一个准确聚焦的成像系统中，射向其他方向的光线将会发生偏转，并且，这些光线最终会被汇聚，从而和通过透镜中心的光线相交于同一点。

图2.9　为了在像平面获得非零的辐照强度，透镜被用于替代理想小孔。一个完美的透镜所生成的图像，和小孔模型所成的像遵循相同的投影公式，但是同时，它聚集了一个面积非零的区域上的光。只有在某一特定距离，透镜才会产生出聚焦良好的图像。

理想透镜有一个缺点，也就是说，它只能被用来汇聚透镜前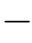z处的点所发出的光。通过我们所熟悉的透镜公式：

我们可以计算出z。其中，z′是像平面和透镜之间的距离，f表示焦距，如图2.9所示^[10]。如果场景中的点和透镜的垂直距离不等于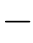z，那么，它们在像平面上所成的像是一个小圆斑；因为从物体表面某一点“出发”的光线，在经过透镜的汇聚后，会形成一个以“聚焦点”为顶点的圆锥，这个圆锥和像平面相交，会形成一个圆斑。

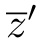我们可以计算模糊圆斑的尺寸。一个和透镜之间的距离为的点所发出的光线，会被聚焦于：距离透镜处的位置，其中，

因此，我们可以得到：如果像平面的位置正好使得：距离透镜z处的点被准确聚焦，那么，距离透镜处的点在像平面上所产生的光斑的直径b为：(www.xing528.com)

其中，d为透镜的直径。

成像域的深度是指：物体能够被聚焦得“足够好”的距离范围，“足够好”是指：模糊光斑的直径小于成像仪器的分辨率。成像域的深度依赖于我们所使用的传感器，但是，不管我们使用什么样的传感器，都有这样的规律：透镜的直径越大，成像域的深度就越小。同时，使用大的光圈会增大聚焦误差。

通过简单的光线传播法则，我们可以理解单透镜的组合。正如我们前面提到的：1)穿过透镜中心的光线不发生偏转，2)平行于光轴的光线将被汇聚于光轴上的一点，并且，该点和透镜之间的距离等于焦距。事实上，这个结论正好就是焦距的定义，也就是说，从无穷远处的物体发出的光线会被透镜汇聚成一点，该点与透镜之间的距离被称为焦距。相反的，位于光轴上的、和透镜之间的距离等于焦距的点所发出的光线，经过透镜后，将在透镜的另一侧发生偏转，成为一条平行于光轴的光线。这个结论可以从光线传播的可逆性得出，也就是说，如果我们将原来的出射光线作为入射光线，那么，新的出射光线就是原来的入射光线。

简单透镜的制作方法是：将透明玻璃的两面打磨成两个球面，光轴即为穿过这两个球面的球心的直线。任何用这种方法做成的简单透镜都会产生缺陷和像差。出于这个原因，人们通常将几个简单透镜组合在一起，仔细地将它们沿着光轴排列起来，做成一个具有更好性质的组合镜。

厚透镜是关于这种透镜系统的一个有用模型，如图2.10所示。我们可以定义两个垂直于光轴的主平面。这两个主平面和光轴的两个交点，被称为节点。进入第一个节点的光线，将沿着相同的方向从第二个节点离开。这定义了组合透镜的投影方式。两个节点之间的距离就是该组合透镜的厚度。我们可以将薄透镜看作是厚透镜的特例，也就是说，让这两个节点重合在一起。

理论上，我们无法做出完美的透镜，不但因为透镜的投影方式不可能和理想小孔完全一样，更为重要的原因是：对所有光线的准确聚焦是无法实现的。这就产生了各种各样的像差。对于一个设计精良的透镜，这些缺陷会被尽可能地做到最小，但是，随着透镜光圈的增大，减少这些缺陷也变得越来越困难。因此，我们需要在光线的汇聚能力和图像的质量之间寻找一种平衡。

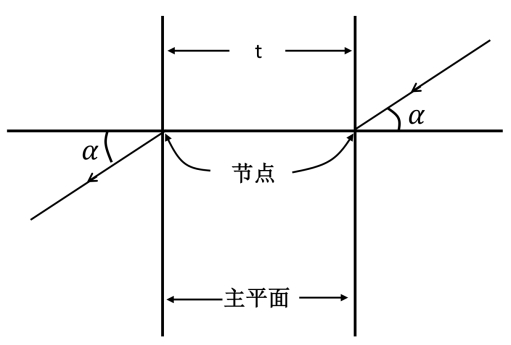
图2.10　理想的厚透镜可以作为：绝大多数实际透镜的一个合理模型。厚透镜的透视投影方式和理想薄透镜是相同的；和薄透镜不同的是，厚透镜会沿着光轴产生一个偏移量：透镜的厚度t。我们可以通过：主平面和节点，来理解厚透镜。节点是指：光轴与主平面的交点。

我们所特别关注的一种缺陷是光晕。想象我们将：一些不同直径的圆形光圈，依次排列在一起，并且，让它们的圆心位于同一条直线上（如图2.11所示）。当你沿着这条公共直线看过去时，最小的光圈将决定你的视野。当你沿着偏离这条线的方向看过去时，一些其他的光圈将会逐渐遮挡你的视野，直到最后你什么都看不见为止。对于一个单透镜来说，进入透镜的所有光线都会被聚焦在图像中；但是，对于一个组合透镜而言，一些透过第一个透镜的光线，可能会被第二个透镜挡住。这取决于：1)入射光线相对于光轴的倾斜程度，以及，2)两个透镜之间的距离。因此，相对于光轴上的点，图像中远离光轴的点的聚光效果会变差，随着该点和图像中心之间距离的增大，其灵敏度也会降低。

此外，随着入射光和光轴之间夹角的增大，透镜的像差会以指数形式增加。像差按其级别进行分类。像差的级别是指：像差与夹角之间的函数关系中所对应的指数（这个函数是一个指数函数）。光轴上的点可能会被很好地聚焦，而本应该被聚焦在图像角落上的点，由于像差的原因，其成像结果将会被“抹成一片”（而不再是一个点）。由于这个原因，在像平面上，只有一个有限的区域可以被用于成像。随着入射光线与光轴之间夹角的增大，像差的大小会以指数形式增加。因此，只使用透镜的中心部分，可以提高成像质量。

图2.11　随着入射光和光轴之间夹角的增大，所能获取到的光的功率将变得越来越小，这种现象被称为光晕。产生光晕的原因是：透镜系统中的小孔阻挡了进入透镜系统的部分光线。由于存在光晕，因此，沿着指向图像区域边界的方向，（成像系统的）灵敏度会发生光滑的（但是有时非常快速的）衰减。

在不需要完全利用成像系统的聚光能力的情况下，我们可以在透镜系统中加入光圈，从而提高成像质量。正如我们已经提到的，固定的光圈挡住了那些和光轴之间有较大夹角的入射光线，使得它们无法穿过透镜而“进入”远离图像中心的区域。这提高了（图像中）远离中心的区域的成像质量，但是，同时也极大地增加了光晕。在绝大多数使用透镜的普通应用中，这并不是一个严重的问题，因为对于图像亮度的光滑的空间变化，人眼是极其不敏感的。但是，对于机器视觉，这却是一个很大的问题，因为我们要通过：对图像亮度的测量结果，来判断场景的亮度^[11]。