平行直线与消失点的关系

对于许多智能光电感知问题，一种重要的研究方法是：

•首先，建立实际应用问题的数学模型；然后，通过数学理论进行模型分析，最后，根据分析结果得出一般结论。

所得到的一般性结论为后续的算法设计奠定了理论基础。

2.2.1　消失点理论

我们将通过消失点问题来阐明上述研究方法。我们的问题是：空间中的一组平行直线所成的图像是什么样的^[3]？为了回答这个问题，我们需要建立相应的数学模型。首先，需要回答如下三个子问题：

1.在数学上如何描述空间中的直线？

2.如何计算空间中直线的图像？

3.如何通过数学分析描述（平行直线的）图像的性质？

对于上述三个问题，第二个问题是直观的，空间中的直线是一系列点(X(t),Y(t),Z(t))T的集合，我们只需要将点(X(t),Y(t),Z(t))T带入式(2.4)，计算出相应的像点(x(t),y(t))T，就得到了空间中直线的图像的解析表达式。因此，解决这个问题的关键在于解决上述第一个问题，具体地说，就是：点(X(t),Y(t),Z(t))T的数学表达形式。

直观上，（三维空间中的）直线是从某一个定点(X 0,Y0,Z0)T=(X(0),Y(0),Z(0))T出发，沿着某一个固定方向(U,V,W)T运动的点(X(t),Y(t),Z(t))T的轨迹。因此，直线的数学表达式为：

或者，写成相应的分量形式：

将式(2.7)带入透视投影公式(2.4)中，就得到了空间中直线的图像：

最后，我们来研究上述第三个问题：通过数学分析描述图像(x(t),y(t))T的性质。生活经验告诉我们，空间直线的像也是一条直线（或直线的一部分，例如射线或一个点），但是，我们很难通过式(2.8)直接看出：(x(t),y(t))T是二维平面上的直线。根据上面给出的三维空间中的直线表达式(2.7)，二维空间中的直线表达式应为：

也就是说，从像平面上某一个定点(x0,y0)T=(x(0),y(0))T出发，沿着某一个固定方向(u,v)T运动的点(x(s),y(s))T的轨迹。根据式(2.8)，可以进一步整理得到：

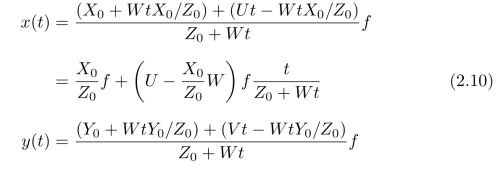
对比式(2.9)，只需令：

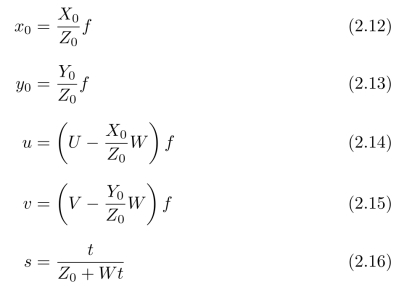
式(2.10)和(2.11)就与式(2.9)匹配一致。因此，

•空间直线的像位于（二维像平面中的）直线上^[4]。

进一步，当W/=0时，可以得到：

于是，根据式(2.10)和(2.11)，我们计算得到：

点(x*,y*)T是空间直线上“无穷远”处的点（即(X(t),Y(t),Z(t))T在t→∞时的点）所对应的像，因此，我们将其称为消失点。注意，（图像上的）点(x*,y*)T与（空间中的）直线(X(t),Y(t),Z(t))T的起始点(X 0,Y0,Z0)T无关，而只是取决于直线的方向(U,V,W)T。注意：从不同的起始点出发、具有相同方向(U,V,W)T的直线构成空间中的一

组平行线，因此，一个自然的结论是^[5]：

•空间中一组平行线的像相交（或汇聚）于消失点(x*,y*)T。

结合上述两个结论，我们通过数学分析，完整地回答了本小节一开始提出的问题：

•空间中的一组平行直线所成的图像是：相交（或“汇聚”）于消失点的一组二维（像平面上的）直线^[6]。

当然，上述结论的成立条件是W/=0，也就是说，空间中的直线不平行于像平面。正如上面指出的，W/=0是式(2.18)及后续分析的前提。当空间中的直线平行于像平面（即W=0）时，所得到的二维直线（即：空间中的一组平行直线的图像）的方向(u,v)T=(Uf,Vf)T是常量（参见式(2.14)和(2.15)），因此，这组二维直线是（像平面上的）一组平行直线。例如：图2.2中的立柱。(www.xing528.com)

通过上面关于消失点的分析，我们了解到了对于光电感知问题的一般研究方法：

2.2.2　寻找消失点

完成理论分析之后，我们需要继续考虑相应的算法实现过程。在很多情况下，我们既不知道空间直线的方向(U,V,W)T，也不知道观测方向（即：相机的光轴方向），因此，无法通过式(2.18)来直接计算出消失点。事实上，对于很多智能光电感知任务，我们所依据的数据就是图像，正如下一小节中将要讨论的，我们试图通过分析图像来求解出观测方向。

我们需要设法直接在图像中（例如图2.3(a)）寻找消失点。上一小节中的理论分析结果为相应的算法设计提供了依据，寻找消失点的问题被分解为如下两个子问题：

1.寻找图像中的长直线；

2.计算长直线的“交点”。

事实上，子问题1已经得到广泛研究，有了解决方案。在第10章中，我们详细讨论了边缘查找方法，图2.3(b)中给出了相应的边缘检测结果。进一步，我们需要根据图2.3(b)中的边缘点，来确定出对应的长直线（由超过一定数目的边缘点所构成的直线），相应的技术被称为Hough变换（参见第10章10.4.3小节内容）。对于一条直线：向量(cosθ,sinθ)T称为：直线的法向量，ρ表示：原点到直线的距离。在第7章7.4小节中，我们还将详细介绍相关内容（参见图7.10）。

图2.3　在图像中寻找消失点。(a)原始图像，包含（空间中）三个方向的平行直线。(b)检测出的边缘点（参见第10章内容）。(c)通过Hough变换，可以确定图中的直线形边缘。(c)通过设置阈值，选择出相应的长直线（大于85个边缘点）。

对于某一个固定的点(x,y)T，式(2.19)中的θ和ρ构成（θρ空间中的）一条正弦曲线：

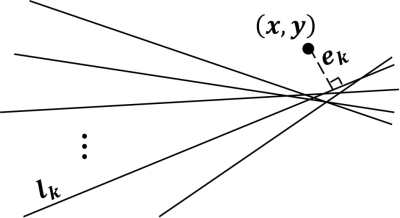
图2.4由于边缘提取和Hough变换过程中的误差，这些长直线并不相交于一点，而是汇聚于一个小区域内。我们可以通过：最小化点(x,y)T到所有直线的距离的平方和，来给出对消失点（在二范数意义下）的最佳估计。

于是，对于图2.3(b)中的每一个边缘点，我们都能画出一条对应的正弦曲线，如图2.3(c)所示。对于某一条固定的直线，其上所有的点具有相同的θ和ρ，也就是说，某一条直线中包含多少个（被检测出的）边缘点，就会有多少条（式(2.20)给出的）正弦曲线相交于图2.3(c)中的对应位置(θ,ρ)T。因此，我们只需要对图2.3(c)中的各个小邻域做统计，即可求得每条（由参数(θ,ρ)T确定的）直线所包含的边缘点数目。图2.3(d)中给出了：边缘点数目大于85的所有长直线（共79条）的对应参数。这79条长直线可以大致分为三组：1)90°＜θ＜60°，2)20°＜θ＜20°和3)30°＜θ＜60°，参见图2.3(d)。

这三组长直线中，每一组所包含的长直线数目分别为：66条，8条和5条。理论上，每一组中的所有长直线（的延长线）应该相交于同一点，但是，由于边缘提取和Hough变换过程中的误差，这些长直线并不相交于一点，而是汇聚于一个小区域内，如图2.4所示。接下来要解决的问题是：如何求这组长直线的“交点”。

空间中的任意一点(x,y)T到第k条长直线x0 cosθk+y0 sinθk=ρk的距离为（参见图2.4）：

我们可以通过：最小化点(x,y)T到所有直线的距离的平方和，来给出对消失点（在二范数意义下）的最佳估计。令：

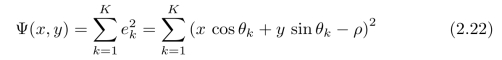
我们可以通过极值必要条件[2]：

来求解最佳估计结果。

进一步，我们可以整理得到：

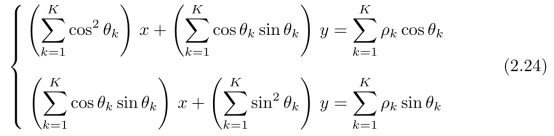
最终，通过求解线性方程组(2.24)，我们得到了图2.3(a)中的（三组空间平行直线所对应的）三个消失点，分别为：

注意，原点在图像的左上角，y轴的方向是向下的。

最后，让我们进一步理解线性方程组(2.24)。一组长直线所对应的方程“合在一起”，构成了如下的线性方程组[2]：

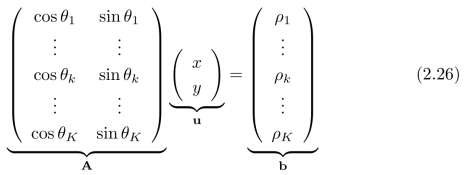
注意，矩阵A并不是一个方阵，因此，我们无法直接通过：求解线性方程组A u=b，来得到消失点的坐标。对比线性方程组(2.24)和(2.26)，不难发现两者之间的关系：式(2.24)可以进一步写为：

如果A T A可逆，那么u=(A T A)-1A T b称为式(2.26)的最小二乘解。