设计永磁机构的分离磁路式7.4.3126kV优化

本节将介绍针对用于本课题组研发的126kV/2500A/40kA型真空断路器永磁操动机构。该操动机构采用分离磁路设计，所配合的灭弧室的主要机械技术参数及断路器要求达到的机械参数见表7-6。

表7-6 126kV/2500A/40kA真空断路器灭弧室的主要技术参数

真空断路器的平均合闸速度定义为：合闸时动、静触头闭合前1/3开距内的平均速度；短燃弧开距速度V₁定义为：动、静触头分开后动触头运动到20mm开距内的平均速度；长燃弧开距速度V₂定义为：动、静触头分开后动触头运动到40mm开距内的平均速度。

1.静态特性计算结果

永磁机构的静态特性是不考虑时间因素时机构的磁场特性和力学特性。机构各部件的材料和尺寸的选择会影响其磁场强度的大小和分布，进而使机构得到不同的分合闸保持力。而永磁机构的动态特性（即分合闸操作过程特性）也是依赖于机构的磁场变化来实现的，可以看作是在不同电流、位置下静态状态的累积。因此，永磁机构静态特性分析是永磁机构机械结构设计的前提，同时也是动态特性分析的基础。

对永磁机构设计来说，首先考虑的为机构的保持力。对于126kV真空断路器，触头弹簧压力为5500N，再加上灭弧室和永磁机构运动部件的重力，保留20%的裕量，永磁机构需要提供7200N左右的合闸保持力。而在分闸位置主要克服灭弧室自闭力和波纹管反力，分闸保持力需要1500±200N。

在尺寸估算的基础上，建立永磁机构电磁场计算模型，通过分析永磁机构尺寸参数对分合闸保持力的影响，并考虑到后续样机更改各种不同零部件尺寸、线圈参数等研究永磁机构特性，设计留有较大裕量来确定永磁机构主要部件的基本设计参数，见表7-7。在该参数下，计算获得永磁机构的合闸保持力7383N，分闸保持力1876N。

表7-7 永磁机构主要部件的结构参数

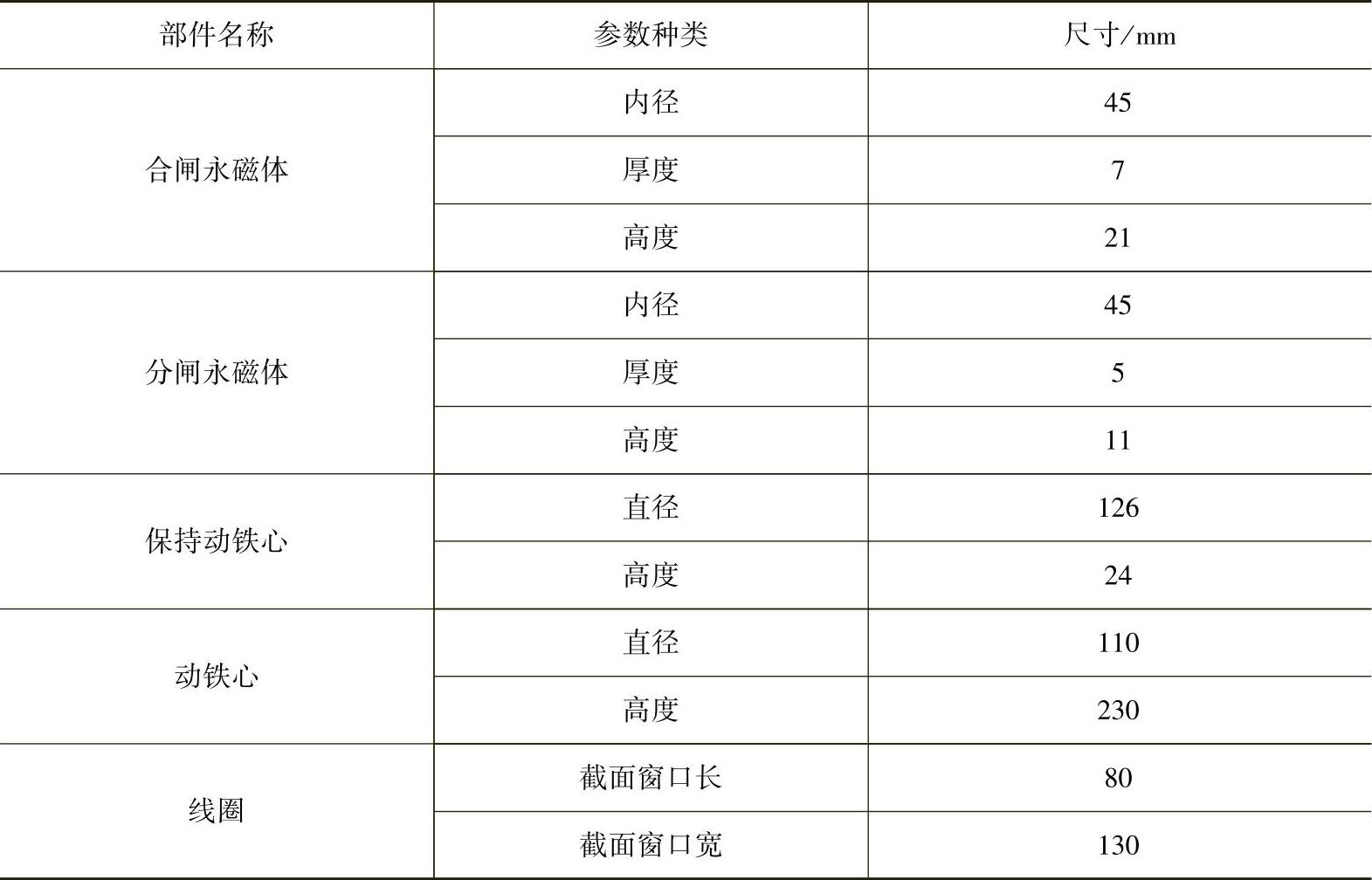
应用参数化建模方法，可以计算不同气隙下永磁体作用磁力的变化和不同电流、不同气隙下线圈电磁力的变化。图7-24所示为永磁体产生的静态吸力与真空灭弧室反力特性的配合曲线。图中显示，在分合闸位置，永磁体产生的吸力均大于反力，故机构能可靠地保持在分合闸位置。从永磁体的吸力特性曲线还可以看出，当保持动铁心离开分、合闸位置时，永磁体的磁力随气隙变化得非常快，也就是说一旦动铁心开始运动，保持力对动铁心运动的阻碍将迅速减小，在几毫米内就几乎不再起作用。

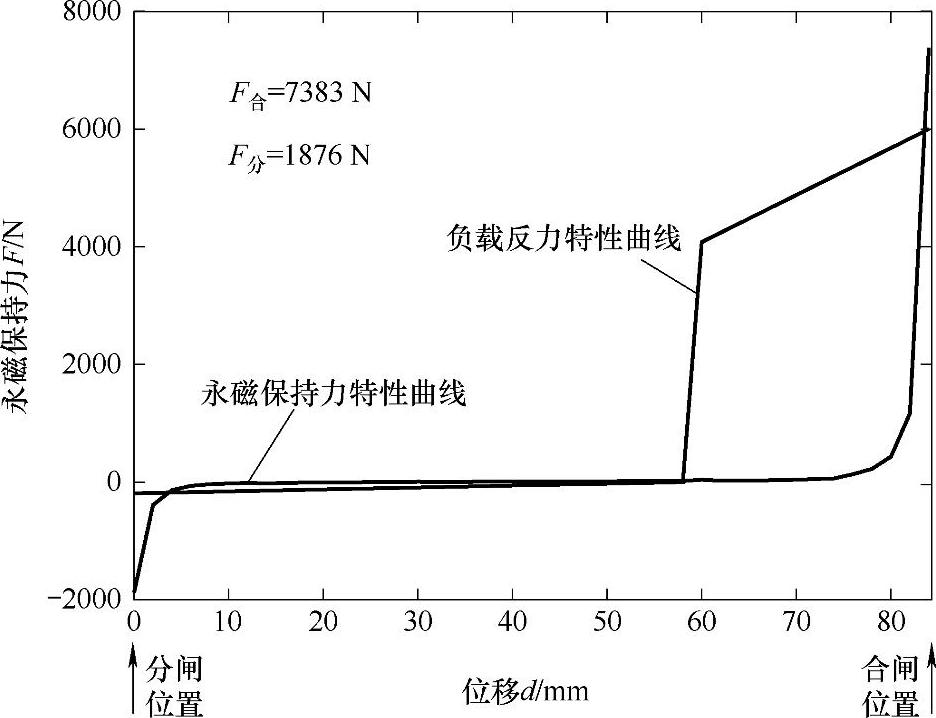
图7-24 永磁体作用下静态吸力随位移的变化

在由静态特性计算确定的永磁机构基本结构参数下，计算获得不同气隙和电流下永磁机构的电磁力和磁链数据。气隙的取值范围为永磁机构的行程，电流的最大值选取要高于静态计算的电流最大值。

2.动态特性计算结果

研究中利用Solidworks软件建立动态系统的三维立体模型，然后将模型导入ADAMS中，添加约束和力等；再利用ADAMS的用户自定义模块，使用FORTRAN语言编写动态特性方程的求解程序，进行永磁机构动态特性的仿真计算。

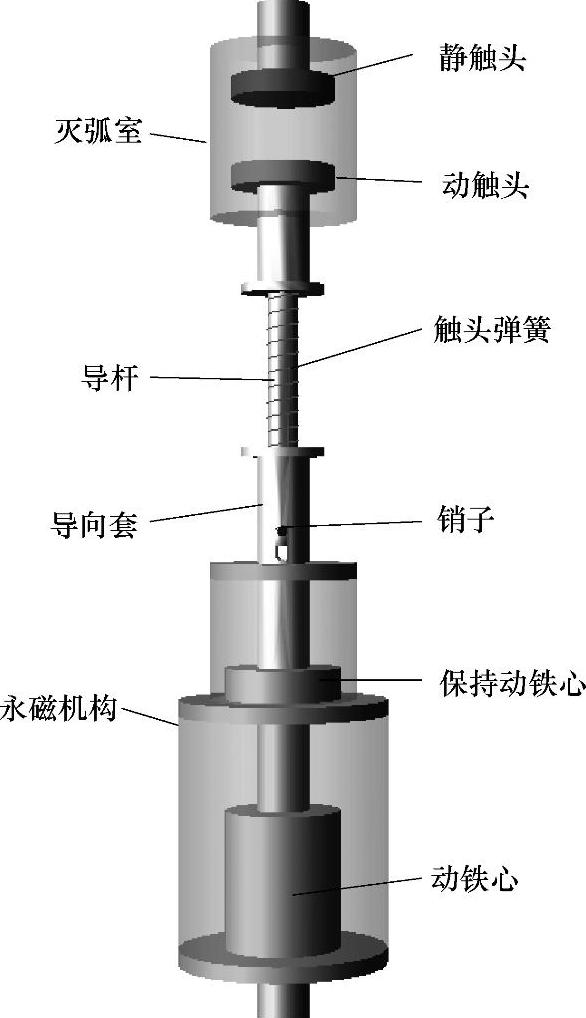
图7-25 动态仿真模型

根据永磁机构动态过程的分析，永磁机构动态过程的机械系统主要包括灭弧室动静触头、永磁机构的动静铁心、触头弹簧以及导杆等。在Solidworks中建立单相开关动态机械系统的仿真模型图，如图7-25所示。模型中对系统进行了简化，仅考虑与机构运动相关的部件，即灭弧室动、静触头，永磁机构动、静铁心，触头弹簧以及连接导杆等。机构的动作过程为：在合闸时，永磁机构动铁心受到电磁力的驱动，通过导向套和导杆带动动触头一起运动。灭弧室动静触头闭合后，动触头、导杆和销子不再运动，动铁心在电磁力作用下与导向套一起压缩触头弹簧，继续向合闸位置运动，直到动铁心与静铁心碰撞闭合为止。分闸时，动铁心在电磁力和触头弹簧作用下与导向套一起向分闸位置运动。当走完超程时，导向套与销子发生碰撞，带动导杆和动触头一起运动，直到动铁心到达分闸位置。将模型导入ADAMS仿真软件中，模型所受力即永磁机构静态计算的电磁力，通过用户自定义函数输入。

动态系统模型的运动是依靠永磁机构提供的电磁力驱动的。电磁力值通过编写程序求解得到。此处在永磁机构静态特性求解的基础上，在FORTRAN编译器中编写了求解电磁吸力的程序，生成链接文件，利用ADAMS软件的用户自定义功能将求解程序导入ADAMS模型中，仿真中通过调用电磁力求解程序为模型加载力约束，电磁力驱动模型运动部件不断改变状态，从而仿真整个运动过程。

126kV真空断路器操动机构仿真参数见表7-8。

表7-8 126kV真空断路器操动机构仿真参数

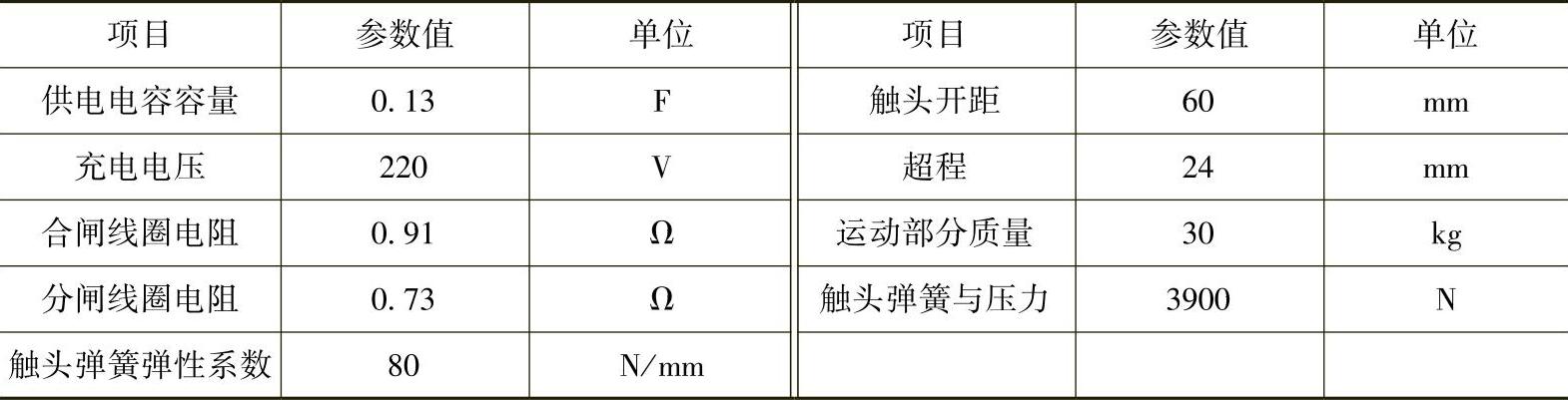
图7-26给出了合闸过程中的动触头位移曲线及线圈电流曲线。从曲线可以看出，动触头平均合闸速度为2.8m/s（刚合前20mm平均值）。而126kV真空断路器对此速度的要求为1.5m/s。从电流曲线可以看出，线圈通电后，电流开始指数上升，到达峰值后，动触头开始运动，电流随之下降。线圈电流的峰值为91A左右。(www.xing528.com)

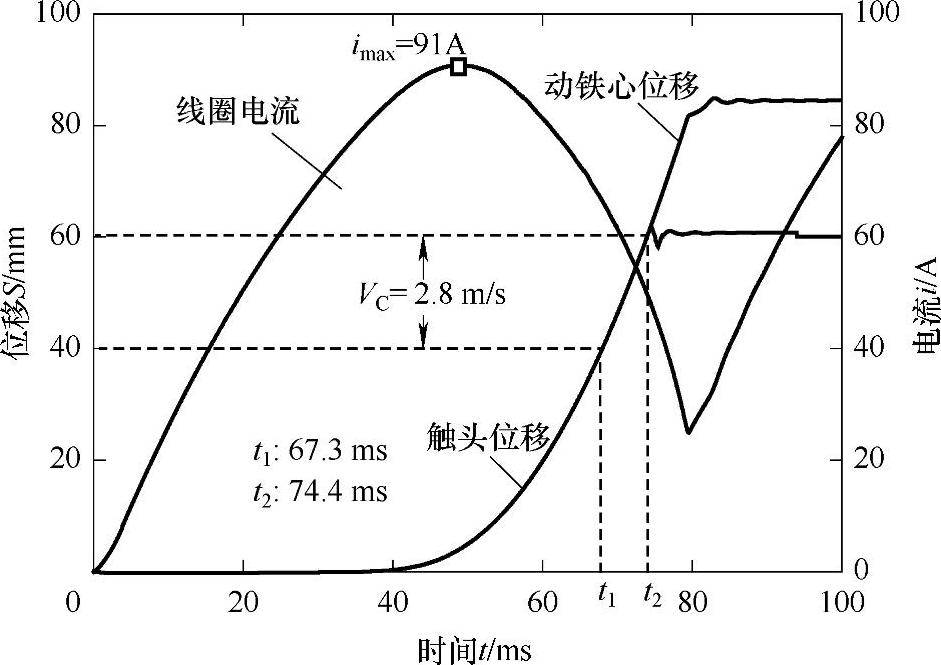
图7-26 合闸过程动触头位移和线圈电流曲线（合闸线圈N=500，D=2.10mm）

分闸过程中的动触头位移曲线及线圈电流曲线如图7-27所示。从图中的分闸曲线可以看出，动触头在刚分后20mm开距内的速度V₁约为3.3m/s，而在40mm开距内的平均速度V₂也约为3.3m/s，满足126kV真空断路器速度要求。在分闸过程中电流到达峰值时触头还没有开始运动，这是因为电流达到峰值时动铁心即开始运动，然而，动触头要等触头弹簧释放完超程后才开始运动，线圈电流的峰值为79A左右。

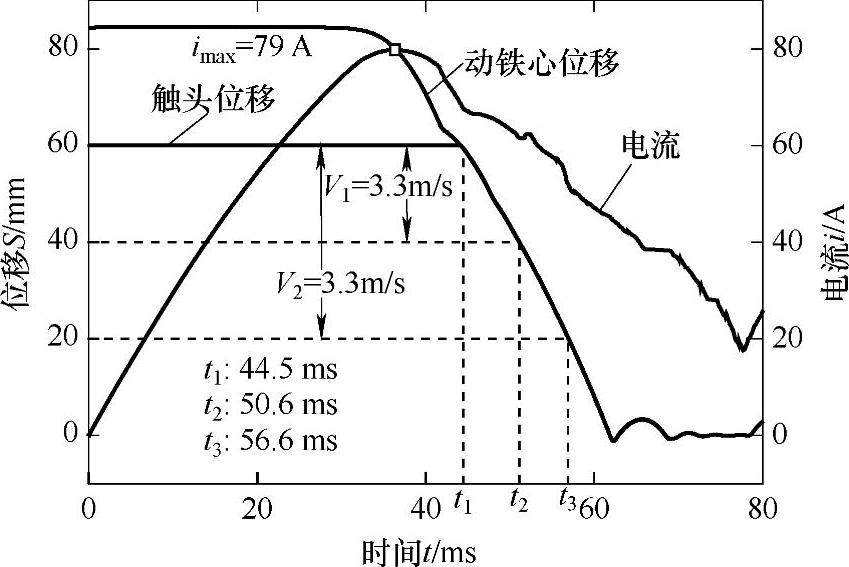
图7-27 分闸过程的动触头位移及线圈电流曲线（分闸线圈N=400，D=2.10mm）

3.可靠性校核

永磁机构保持部分动铁心和静铁心在机构分合闸过程中会产生比较大的动态冲击力，该力值显著高于其静态保持力。保持动铁心表面在该动态冲击力作用下会产生变形，使其之间产生较大气隙，进而造成静态保持力变小。同时，冲击力过大还可能会造成机构部件或真空灭弧室承受超过强度极限的瞬时力而产生变形或断裂，在多次分合闸操作后造成部件的疲劳破坏。另外，与传统结构形式永磁机构不同，新型分离磁路永磁机构因永磁体安装于保持静铁心和动铁心之间，过大的冲击力还可能造成永磁体断裂，进而影响机构的可靠性。因此，基于碰撞特性的机械可靠性研究具有重要的理论意义和实际应用价值。

ANSYSLS-DYNA是通用非线性动力分析有限元软件，适合求解各种二维、三维非线性结构的爆炸、高速碰撞等非线性的动力学冲击问题。此处采用Workbench中Explicit Dynamics模块对其动态过程进行计算，仿真流程图如图7-28所示。

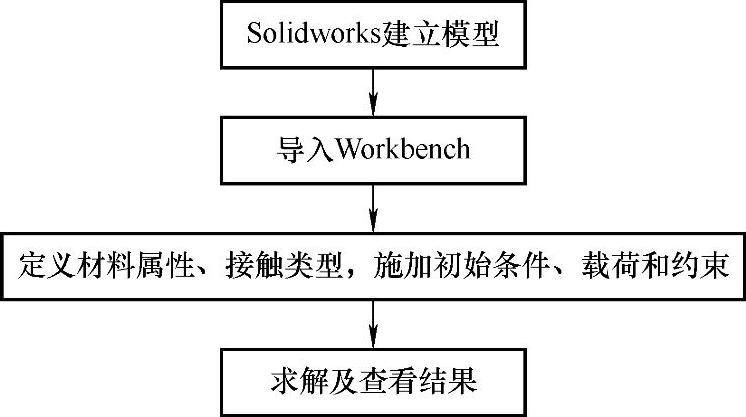
图7-28 永磁机构动态冲击过程流程图

在Solidworks中建立分离磁路永磁机构的模型，如图7-29所示。由于只考虑保持部分碰撞特性，为方便计算，模型仅考虑保持部分和电磁操动部分与运动相关的组件，其余部件忽略。仿真中用到两种材料，即动铁心和静铁心所用的电工纯铁DT4E、永磁体钕铁硼（NeFeB）稀土永磁材料。材料模型采用双线性各向同性硬化模型（BISO），定义参数包括：密度（DENS）、弹性模量（EX）、泊松比（NUXY）和屈服应力（Yield Stress），材料参数见表7-9。

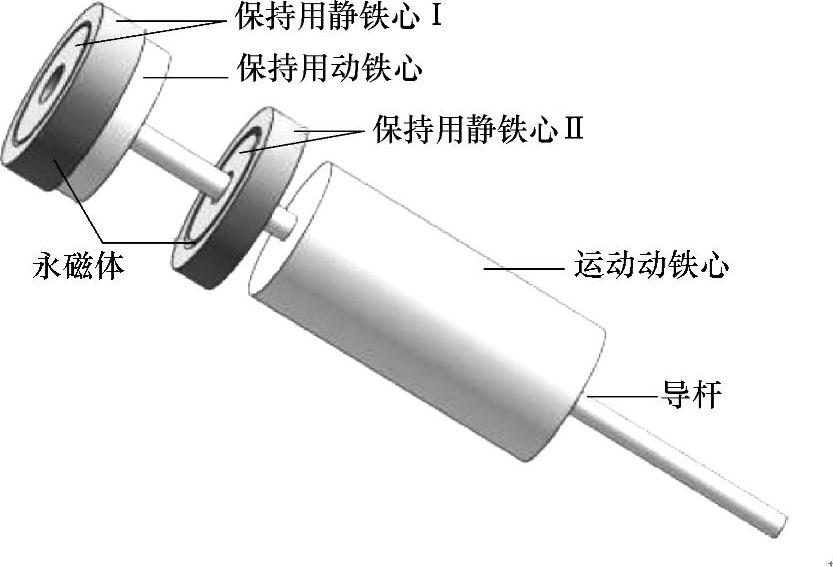
图7-29 分离磁路永磁机构碰撞特性模型

表7-9 材料参数

定义各部件之间的接触类型，以平均分闸速度为2.5m/s和平均合闸速度为1.5m/s对机构进行可靠性分析。以分闸过程为例，赋予运动部件初始速度为2.5m/s，动静铁心间初始永磁保持力为2000N，碰撞力仿真结果如图7-30所示，最大碰撞动态力峰值为300733N。

在该作用力下，分闸保持静铁心外部和内部的最大应力分布为151MPa和165MPa，电工纯铁的屈服强度为117MPa，该值虽低于最大应力强度（在分闸速度2.5m/s下），但作用时间短，且最后碰撞时速度可能低于该速度值。

对于合闸过程，赋予运动部件初始速度为1.5m/s，动静铁心间初始永磁保持力为7200N，在该初始条件下计算得到碰撞力，分闸保持静铁心外部和内部的最大应力分布为25.5MPa和24.1MPa，明显低于最大应力强度。

根据国标GB1984—2014规定的M2级机械寿命要求，126kV真空断路器机械寿命为10000次，故只要永磁机构机械寿命能达到或超过10000次，即不会对整机机械可靠性产生影响。

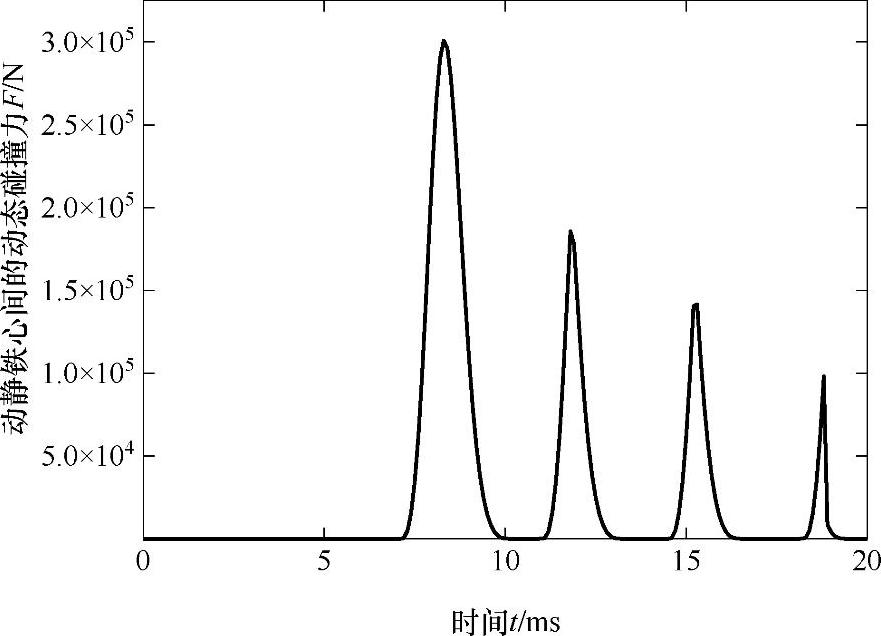
图7-30 分闸过程铁心间动态冲击力仿真结果（V_分=2.5m/s）

以上述仿真获得分、合闸过程动态冲击力曲线为应力谱曲线输入，采用nCode Designlife对永磁机构在分闸速度V_分=2.5m/s和合闸速度V_合=1.5m/s状态下的机械寿命进行分析，最容易损坏的静铁心内部组件疲劳寿命为17710次，即在该分闸速度碰撞下，静铁心外部组件在操作17710次后失效。该值明显高于国标GB1984—2014规定的M2级机械寿命要求，故该机构设计能满足126kV真空断路器可靠性要求。