永磁操动机构特性计算与设计

1.永磁机构设计的基本方法

永磁机构的设计要从真空断路器对永磁机构特性的要求出发。在稳态时，永磁机构通过永磁体提供的保持力使动触头稳定地保持在分、合闸位置。在分闸位置时，主要需要克服波纹管自闭力，合闸位置主要需要克服触头弹簧反力；运动时，永磁机构动铁心通过导杆带动动触头运动，运动速度要满足动触头分/合闸速度和刚分速度的要求，保证真空断路器可靠动作。图7-17为永磁机构的设计流程，静态特性计算解决在稳态条件下，永磁体所产生的磁场分布和磁力大小以及线圈产生的电磁吸力与气隙之间的关系，由此确定永磁机构的基本结构和尺寸，并为动态特性计算奠定基础。动态特性计算分析运动过程中触头位移速度，机构线圈电流和控制电路的参数。根据计算的结果优选出既能满足开关分、合闸速度要求，又能使励磁电流小的设计参数，减小控制电路的负担，降低成本。将动态特性计算得到的分合闸速度作为机构冲击响应，得到机构碰撞冲击载荷，连同机构静态特性计算得到的保持作为静态应力，计算得到机构的疲劳寿命，并对其可靠性进行评估。

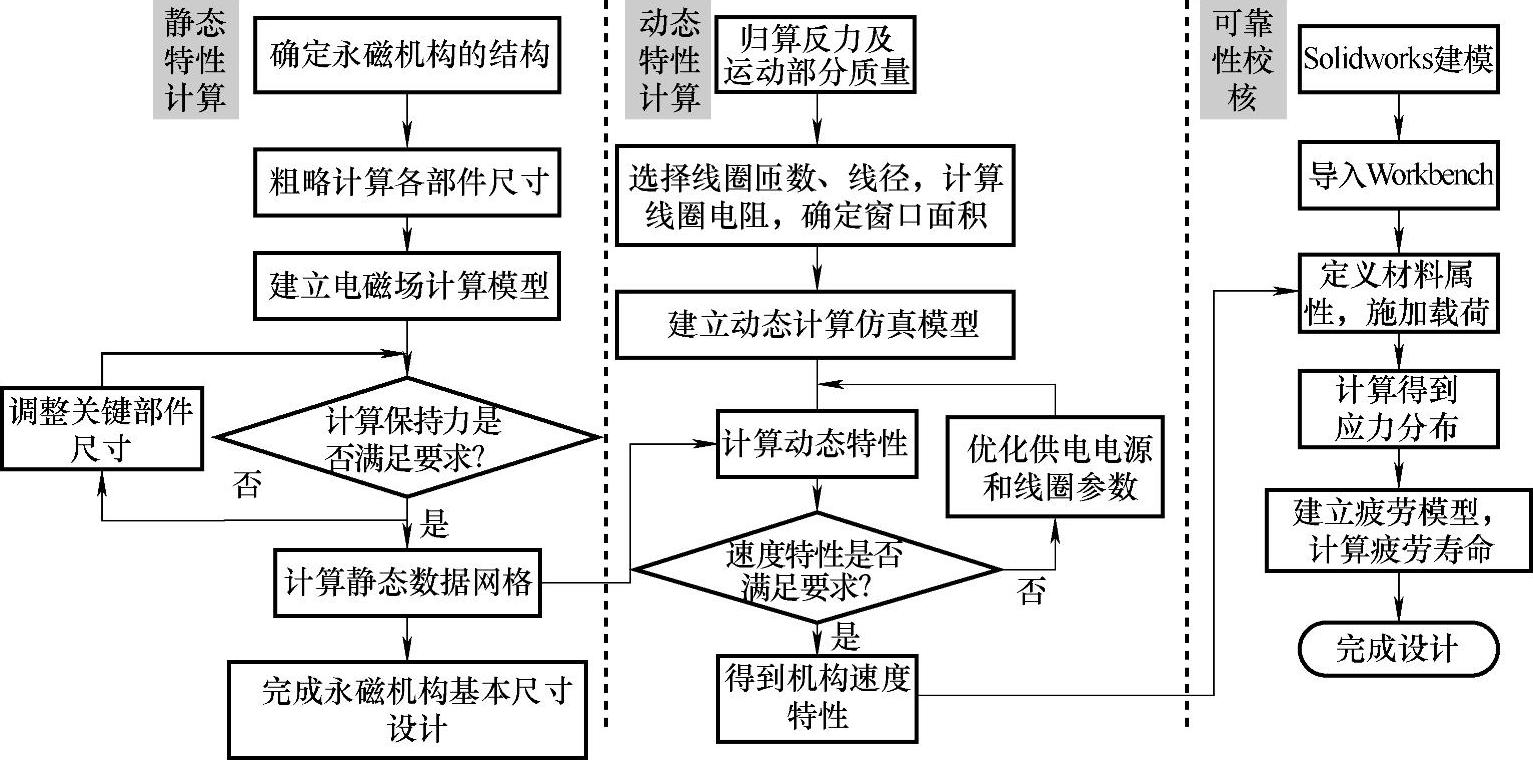
图7-17 永磁机构的设计流程

（1）静态特性计算

永磁机构静态特性矢量磁位A应满足

式中 J——源电流密度；

μ——磁导率。

对于圆形机构，在圆柱坐标系下采用轴对称场计算，得到

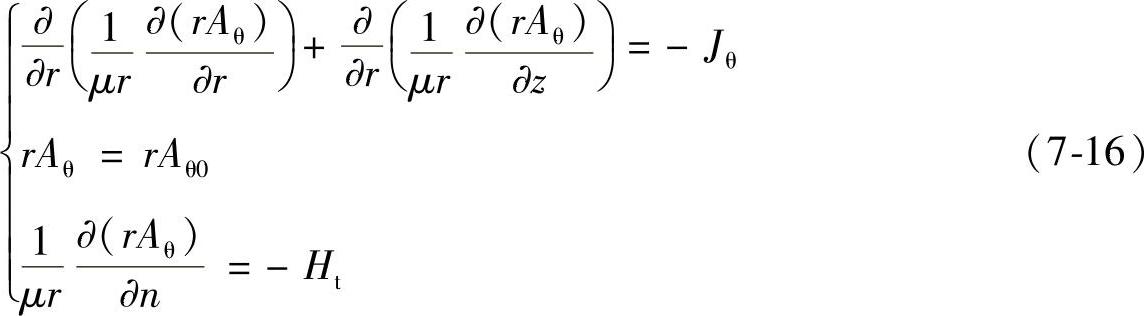
在电磁场计算时，采用面电流模型模拟永磁体。永磁体经过充磁，具有剩余磁化强度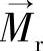，它的特性满足

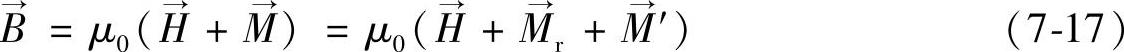
式中 μ₀——真空的磁导率；

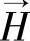——永磁体工作点的磁场强度；

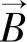——永磁体工作点的磁感应强度；

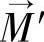——永磁体的感应磁化强度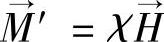，，χ是永磁体的磁化系数，与相对磁导率的关系为μ_r=1+χ

因此，式（7-17）可写为

对于均匀磁化的永磁体，其内部各点的剩余磁化强度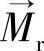大小相等方向相同，而在永磁体外部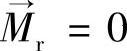，因此可以认为在平行于的永磁体侧面上，存在等效的面电流。等效面电流密度表示为

式中 ——永磁体平行于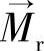侧面外法向单位向量。

永磁体等效面电流侧与其他介质交界面处的边界条件为

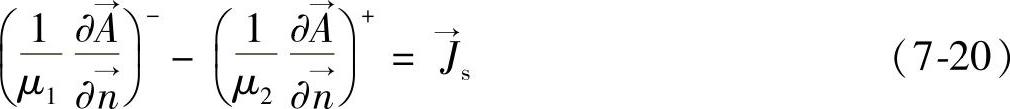
永磁机构的电磁吸力由永磁体和励磁线圈产生并作用在动铁心上。计算时在动铁心的外围取任一闭合面S，通过对S面上的应力求解面积分获得电磁吸力值，即

式中 p——气隙单元E中的表面应力，即

式中 B——单元E中的磁感应强度；

n——沿积分表面S法线方向的单位向量。

通过对所有离散单元电磁力求和，获得总的电磁吸力为

式中 ΔS_E——单元E中沿积分途径的表面积；

p_E——单元E的表面应力。

（2）动态特性

永磁机构的分闸操作和合闸操作，其线圈电流的变化过程可以分为两个阶段：一是励磁电流接通后动铁心开始运动前，电磁力小于动铁心所受吸力，动铁心不运动，线圈电流由零开始逐渐增大；第二阶段是电流增大到一定值时，电磁力大于动铁心所受吸力，动铁心开始运动，同时线圈中产生反电动势，抑制线圈电流的增长，线圈电流逐渐下降，直至动铁心走完全部行程到达终点。如果此时，线圈的励磁电路还未关断，线圈仍处于通电状态，线圈电流则由于动铁心已经静止，电流又开始上升，产生所谓的“马鞍形”电流。

永磁机构的电容放电励磁电路如图7-18所示，其中C为充电电容，L和R分别为线圈的等效电感和等效电阻。

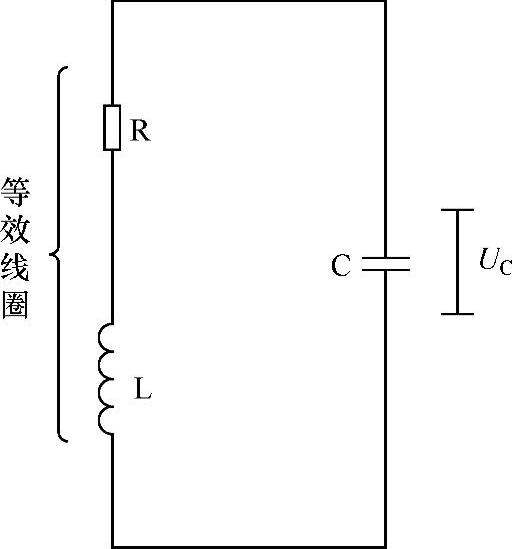
图7-18 电容励磁电路

永磁机构动态过程在电路上必须遵循电压平衡方程，在运动上遵循达朗贝尔运动方程，在磁场上必须遵循麦克斯韦方程，在热路上遵循热平衡方程，这些方程间存在相互联系，构成了描述动态过程的微分方程组。由于动态过程历时极短（一般机构动作时间为几十毫秒），电磁系统又存在热惯性，所以热变化很小，可忽略不计，那么描述永磁机构动态特性的状态方程组为

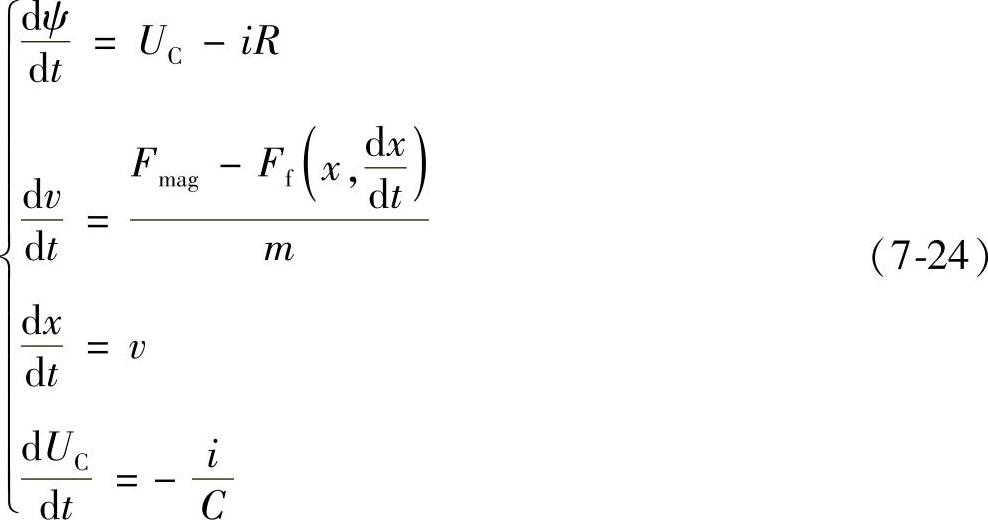
式中 v——运动部件的运动速度。

式（7-24）中各参量的初始条件为

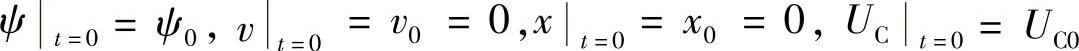
对式（7-24）所述的电路方程、电磁场方程和运动方程耦合求解，即可以获得永磁机构的动态特性。

对微分方程组在初始条件约束下进行数值求解，即可以获得该永磁机构在一定具体条件下的实际动态特性。在求解动态特性前，应先用ANSOFT软件计算永磁机构的静态特性，求解永磁机构动铁心在不同位置和不同线圈电流下所对应的电磁力和磁链数据，建立F=f（i，x）、ψ=ψ（i，x）的数据网格，然后将电磁力、磁链与气隙、电流的关系转化为F=f（ψ，x），i=g（ψ，x），最后利用Runge-Kutta法求解动态特性的状态方程组。

（3）可靠性

为验证该永磁机构主要部件的机械可靠性，此处基于金属材料S-N曲线及应力-应变有限元分析结果，采用Ncode-DesignLife软件，对126kV真空断路器永磁操动机构易损部件的疲劳寿命进行仿真计算。考虑到126kV真空断路器动作次数较少，该过程具有低周疲劳特征，故采用基于最大应力应变的低周疲劳分析方法，对永磁机构进行疲劳强度分析及寿命估算。该方法的基本思想认为零件或构件的整体疲劳性能取决于最大应力-应变状态和特征，即如果机构能通过最大应力-应变考核，其机械可靠性更好。

在计算永磁机构疲劳寿命时，施加载荷除永磁机构静态保持力外，还需加载机构碰撞时动静铁心之间的动态碰撞力，该力通过动态特性计算得到。在该动态碰撞力和静态保持力作用下，求解得到永磁机构各部件的等效应力分布，进而得到机构疲劳寿命。

根据低周疲劳寿命分析理论，等效应力其值为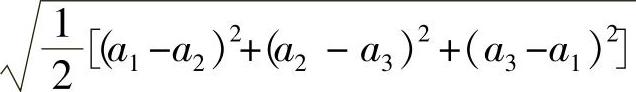，其中a₁，a₂，a₃分别指第一、二、三主应力。该等效应力是用应力等值线来表示模型内部的应力分布情况，它可以清晰地描述一种结果在整个模型中的变化，从而使分析人员可以快速地确定模型中的最危险区域。材料在低周疲劳过程中，其应力应变行为可用滞后回线表征，如图7-19所示。每一应力产生的总应变为

Δε=Δε_e+Δε_p （7-25）

式中 Δε——总应变；

Δε_e——弹性应变幅度；

Δε_p——塑性应变幅度。(www.xing528.com)

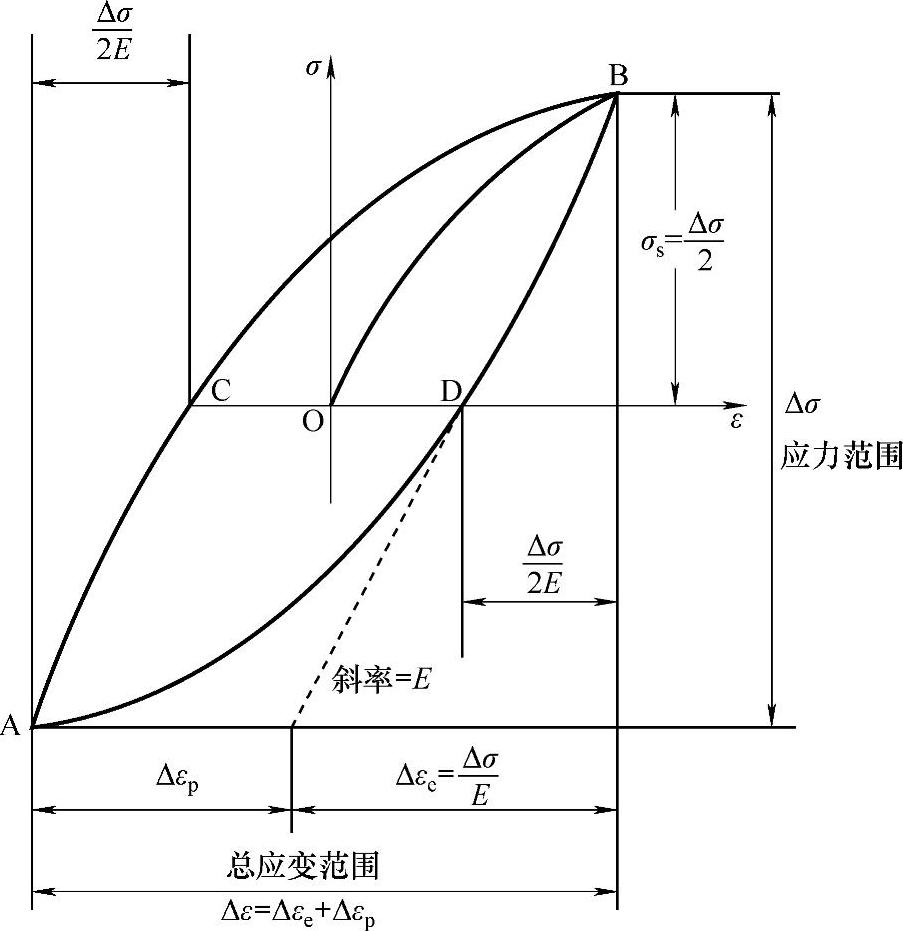
图7-19 应力应变滞后回线

弹性应变幅度Δε_e和塑性应变幅度Δε_p如下：

式中 σ′_f——疲劳强度系数；

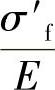——循环数N=1/2处直线2的总坐标斜率；

b——疲劳强度指数，直线的斜率；

E——材料的弹性模量；

ε′_f——疲劳塑性系数，N=1/2处直线1的纵坐标截距；

c——疲劳塑性指数。

总应变-寿命曲线数学表达式为

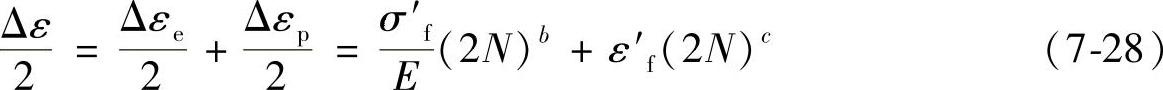
结合材料的疲劳强度系数σ′_f、疲劳强度指数b、疲劳塑性系数ε′_f、疲劳塑性指数c和材料的弹性模型E，可得到材料的总应变-寿命曲线特性。

2.永磁机构的反力特性

永磁机构的反力主要有触头弹簧力、灭弧室自闭力、机械摩擦力和运动部件重力，这些力在机构运动过程中有时是阻力，有时是动力。触头弹簧力仅在动铁心运动在触头超行程阶段时起作用。由于该机构为直动机构，故不考虑反力及质量归算问题。触头弹簧力为

F_c=F₀+K（R-R₀） （7-29）

式中 F₀——触头弹簧预压力；

K——弹簧刚性系数；

R——弹簧最终长度；

R₀——弹簧初始长度。

灭弧室自闭力一般在200N左右，力的方向指向合闸方向。摩擦力主要由加工安装工艺决定，在此可忽略不计。机构运动系统重力则由重力公式G=mg计算得到，m为运动部分总质量。归算后的反力特性如图7-20所示。

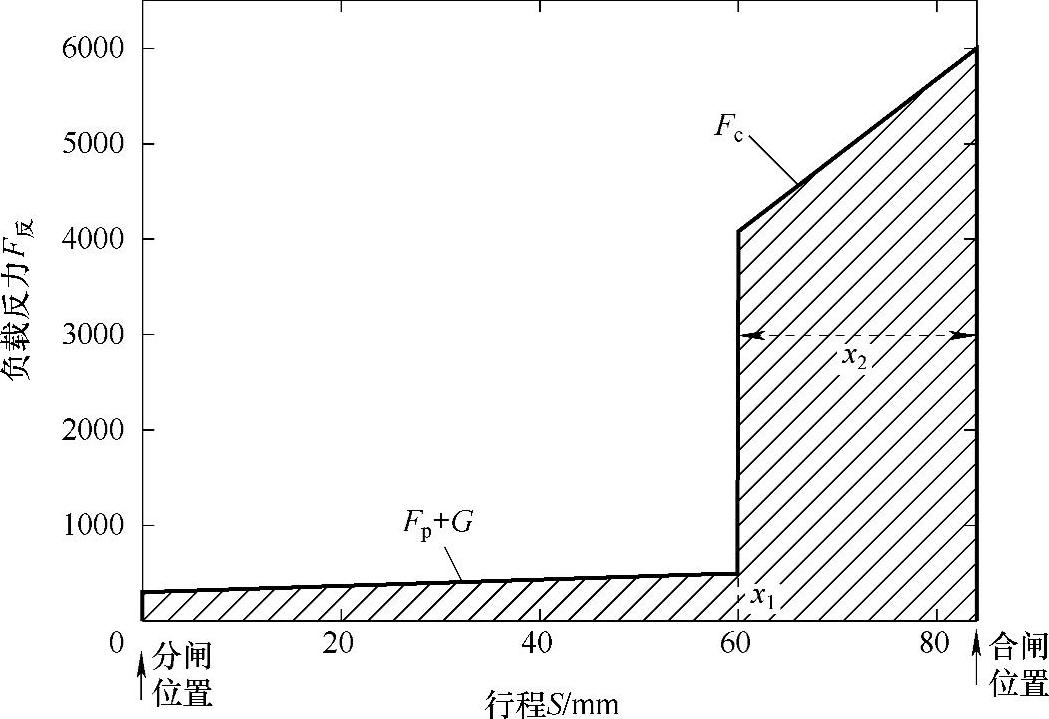
图7-20 归算到动铁心的反力特性

F_p—灭弧室自闭力 F_c—触头弹簧反力 G—运动部件重力 x₁—触头开距 x₂—触头超程

3.经验公式尺寸估算

确定永磁机构的结构形式后，根据真空灭弧室负载特性，得到机构所需提供的合闸保持力。在工程实际应用中，至少考虑20%的裕量。双稳态永磁操动机构的结构设计主要包括：动铁心直径、永磁体位置及尺寸、分/合闸线圈参数、动铁心质量等。

（1）动铁心

设计永磁机构各部件的尺寸大小时，合闸保持力能否满足要求是首要考虑的因素。在满足性能要求的前提下，要考虑如何调整结构参数，使永磁机构体积最小、性能最优。在设计初始阶段，各部分零件的尺寸可以粗略估算。其中，动铁心尺寸是首先可以确定的参数，动铁心在磁场中受到的磁力可表示为式（7-21）。

磁通密度B数值大小的选取会影响永磁机构整机的大小，为满足断路器小型化的发展要求，尽量使铁磁材料工作到其磁化曲线的拐点附近。对于电工纯铁DT4E来说，B值为1.6～1.7T。根据永磁机构侧的反力特性，动、静铁心之间至少产生7000N的力，可得动铁心的直径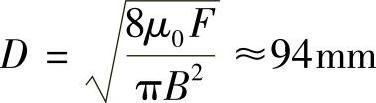，因此，合闸时气隙磁通。

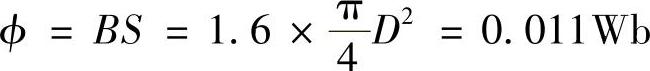（2）永磁体

钕铁硼永磁体工作点在一条直线上，当永磁机构在合闸位置时，永磁体的工作点B≈0.96T。永磁体总的截面积可由公式S=ϕ/B求得。在确定永磁体位置后，即可估算得出永磁体高度和厚度。

（3）线圈安匝数NI

对于合闸线圈，在合闸过程中，机构动铁心需克服分闸保持力向合闸位置运动，所以合闸线圈在分闸位置应提供的磁场强度B可由式（7-22）得到。分闸线圈安匝数可通过同样方法初步估算。

综上所述，通过上述经验公式可获得机构的初步尺寸，但因为经验公式在计算时忽略了磁场的不均匀性、线圈电流和电感等的变化，所以经验公式获得尺寸仅能作为有限元仿真建模的基础，后需通过有限元建模对机构尺寸进行优化设计。

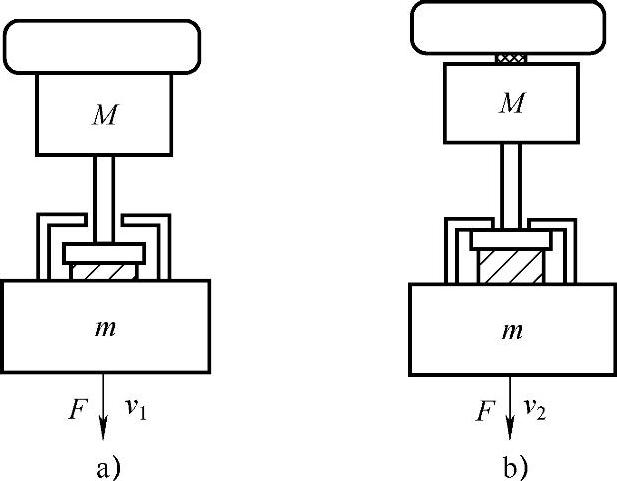
图7-21 分闸过程碰撞示意图

a）碰撞前 b）碰撞后

4.动铁心质量的确定原则

由上述分析可知，永磁机构分闸过程示意图如图7-21所示。图中M为灭弧室侧运动部分质量（在此简化为动触头质量），m为机构侧运动部分质量（在此简化为动铁心质量）。在线圈电流驱动下，动铁心m在电磁力F和触头弹簧力的作用下运动，当动铁心走完超程时，速度达到v₁，此时，触头弹簧力消失，动铁心m将带动动触头M一块向下运动，此时动铁心和动触头运动速度为v₂。这个过程时间很短，忽略重力和摩擦力的影响，认为该过程在碰撞瞬间满足动量守恒定律，即

由于对于高电压等级真空断路器，需要较高的刚分速度，即希望v₂尽可能大。考虑到在动触头运动前，机构运动速度与动铁心质量m有关，故仿真得到不同动铁心质量m时，在动铁心带动动触头运动前的v₁，通过拟合，得到v₁=v₁（m）的函数关系满足

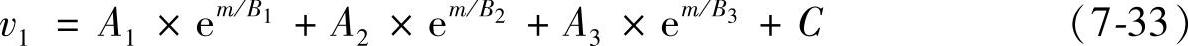
式中 A₁，A₂，A₃，B₁，B₂，B₃，C——常数，与机构属性有关。

将式（7-33）代入式（7-32），得

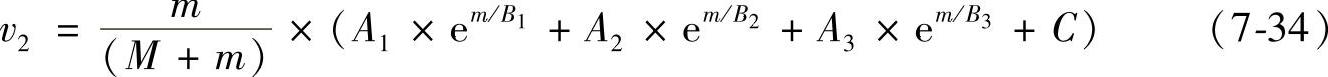
对于该分离磁路永磁机构，通过计算得到动铁心带动动触头运动前的速度v₁与动铁心质量m之间的关系如图7-22所示，满足式（7-35）。

v₁=2.4509×e^m/-8.1029+2.4509×e^m/-9.00277+2.4509×e^m/-9.90305+2.94203 （7-35）

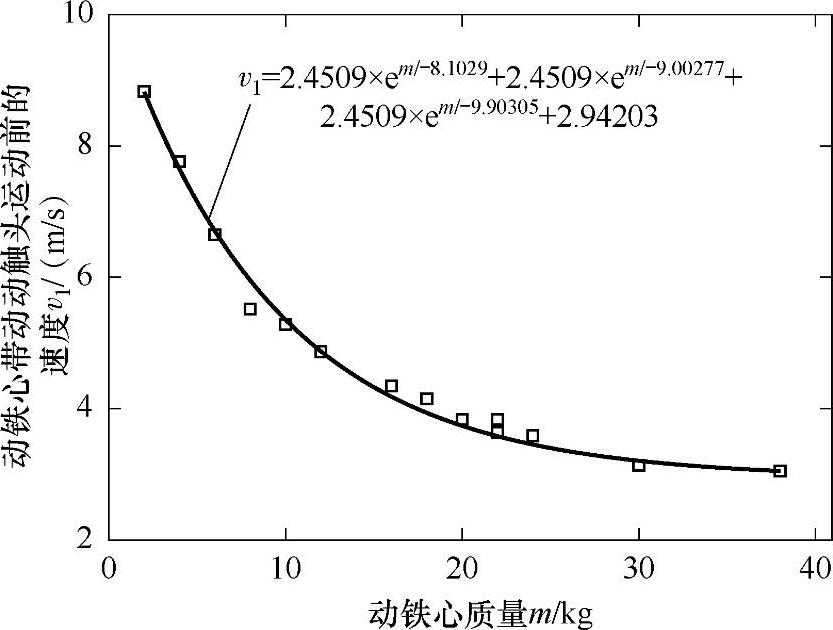
图7-22 动铁心带动动触头运动前的速度v₁与动铁心质量m之间的关系

把式（7-35）代入式（7-32），通过M取不同值，得到动铁心质量m与动触头刚开始运动速度v₂的关系如图7-23所示。

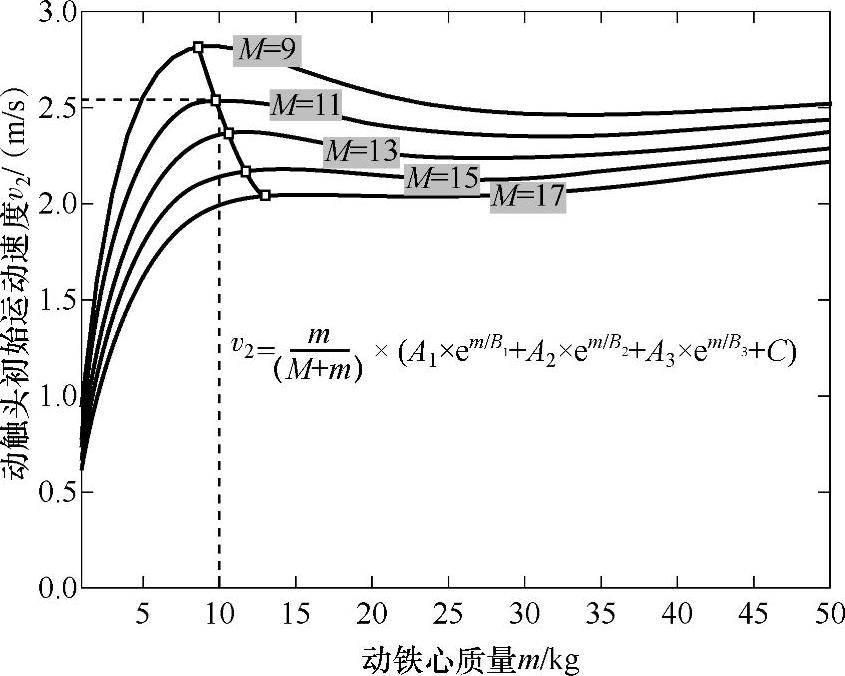
图7-23 动触头初始运动速度v₂与动铁心质量m的关系