不规则凸轮廓线的计算与设计

1.凸轮廓线计算的实现

在CT20弹簧操动机构中，凸轮的结构为滚轮摆动从动件结构，图7-9为滚轮摆动从动件盘形凸轮的计算原理图。由7.2.2节计算出凸轮机构输出轴转角与储能轴转角之间的关系后，凸轮轮廓线的极坐标可以通过式（7-12）与式（7-13）得到：

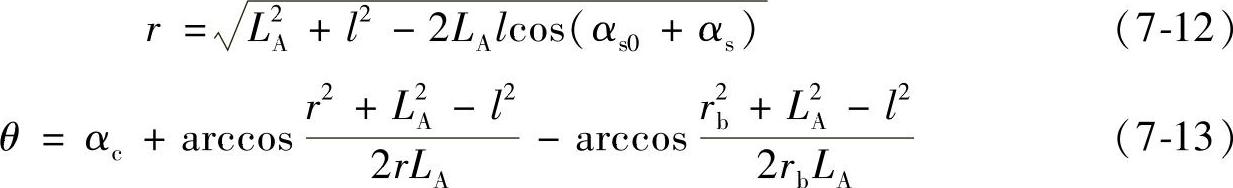
式中 r——凸轮轴心与滚轮中心的中心距；

θ——轮廓线的展角；

α_c——凸轮的角位移；

L_A——凸轮轴心与输出轴的中心距；

l——摆杆的长度；

α_s——摆杆的角位移；

α_s0——摆杆起始的位置角。

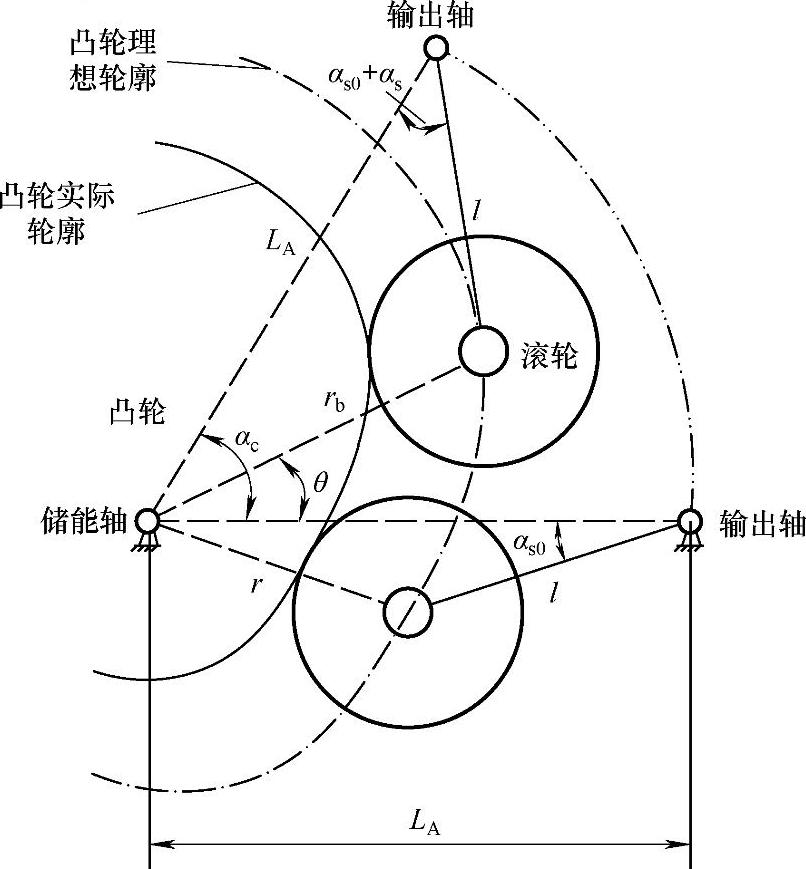
图7-9 滚轮摆动从动件盘形凸轮的计算原理图

通过式（7-12）和式（7-13）便可以求出在极坐标下凸轮理想廓线上各点的坐标。所谓凸轮的理想廓线，即凸轮从动滚轮的圆心在围绕凸轮旋转一周后的轨迹，它与凸轮的实际轮廓线是属于等距曲线。因此，计算出凸轮的理想廓线后，通过等距曲线的坐标换算公式，便可以求得凸轮的工作廓线的极坐标。

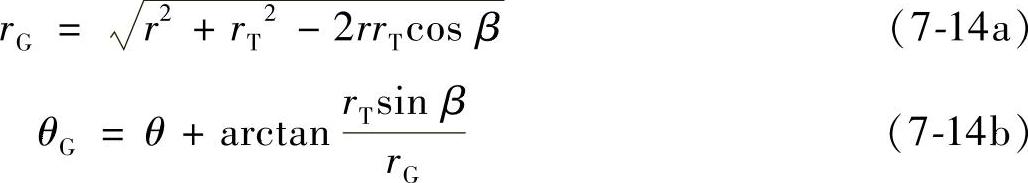
式中 r_G——凸轮工作廓线的半径；

θ_G——对应r_G的凸轮摆角；

β——向径r与公法线n-n的夹角。

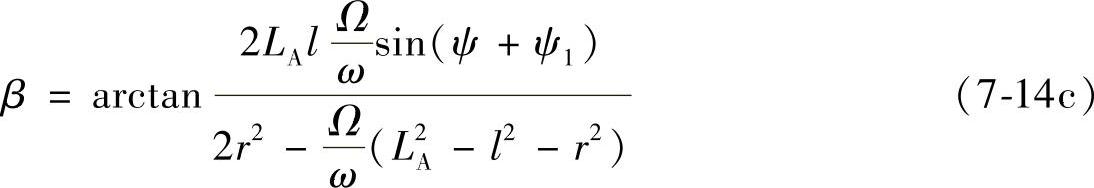(www.xing528.com)

式中 Ω——摆角从动件的角速度；

ω——凸轮转动的角速度。

根据已知条件，由式（7-14a）、式（7-14b）和式（7-14c）顺次计算出凸轮工作廓线各点的极坐标值。至此，在整个合闸过程中，凸轮的实际轮廓线就可以计算出来了。

2.设计实例结果

按照上述设计方法对126kV真空断路器配CT-20弹簧操动机构的凸轮机构进行设计。目标合闸行程曲线如图7-10所示。由图中可见，触头的行程为60mm，超程为20mm。触头接触前4mm的平均速度为1.15m/s。通过上述方法得到的凸轮模型，如图7-11所示。

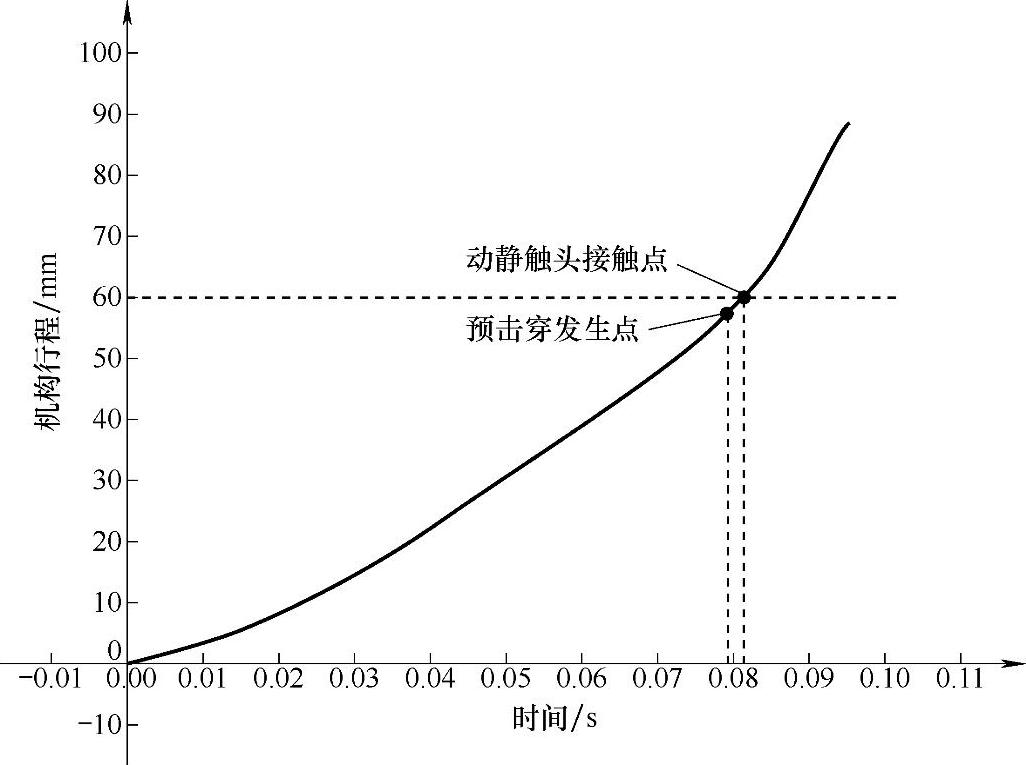
图7-10 目标合闸行程曲线

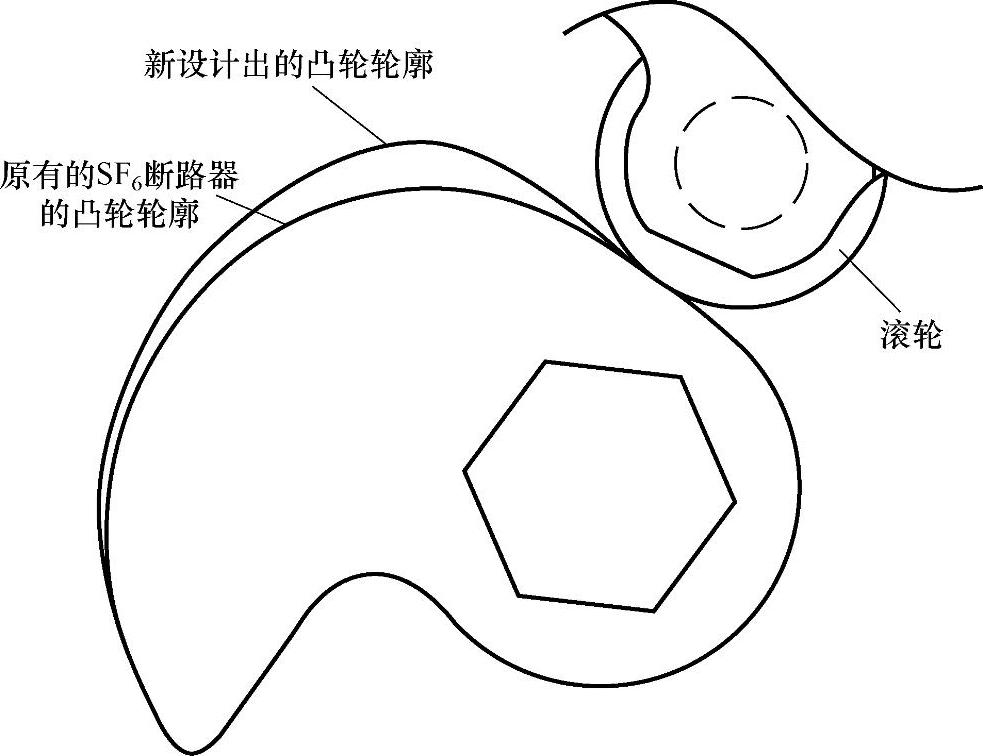
图7-11 使用新设计方法设计出的凸轮轮廓

图7-12为两种凸轮的输出力矩与输电等级真空断路器的负载力矩的关系。从图中可以看出，新设计的凸轮的输出力矩比SF₆断路器上使用的凸轮与真空断路器负载力矩曲线更加相匹配。该凸轮在机构行程60mm开距过程中，以较小的能量达到了合适的平均合闸速度，有效减小了合闸弹跳，而在触头弹簧储能的过程中加大了输出的力矩，使得机构能轻松地克服触头弹簧的阻力。

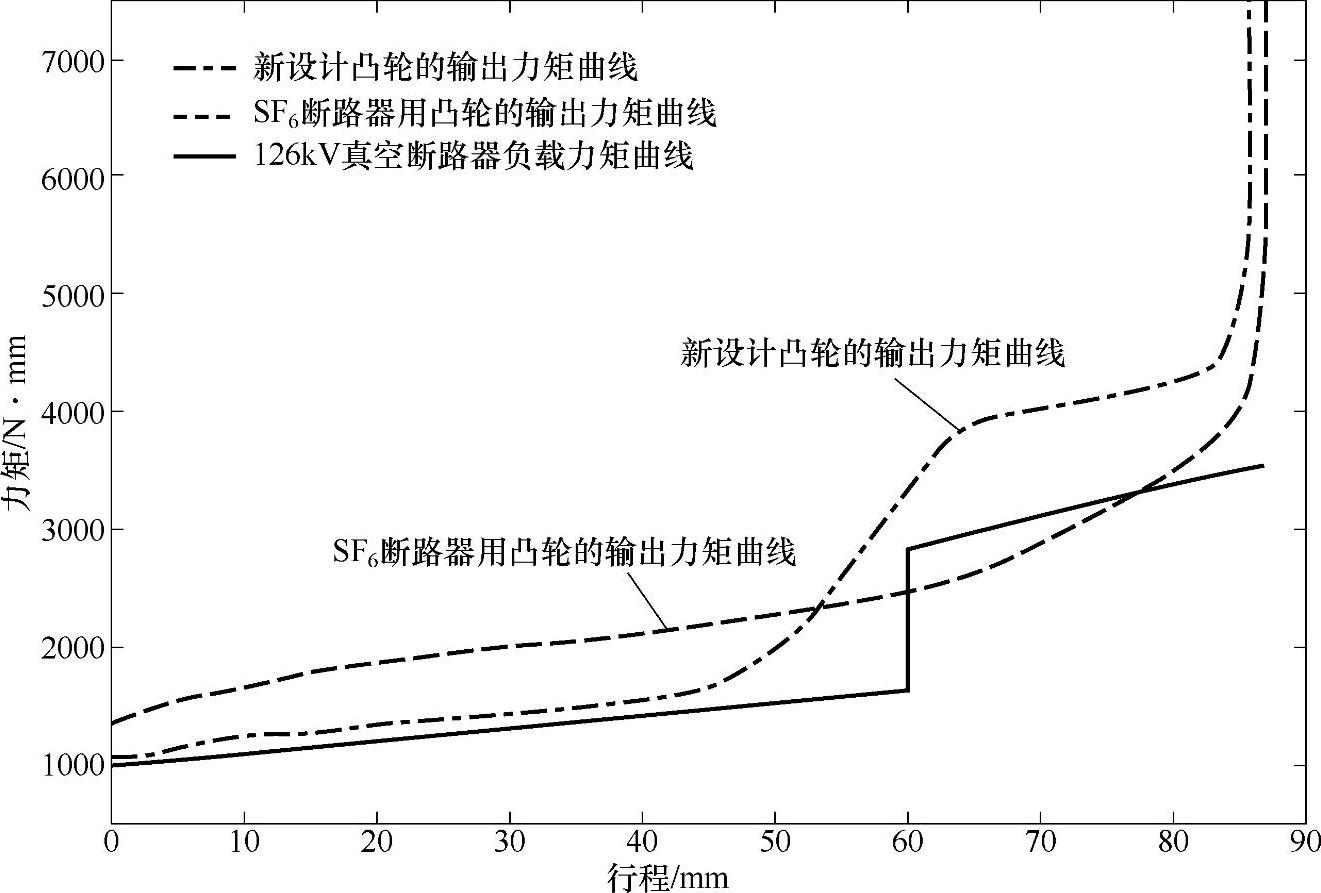
图7-12 两种不同凸轮的输出力矩曲线

将安装了这两种凸轮的126kV真空断路器的虚拟样机模型在ADAMS软件中进行仿真计算，可以得到两种不同的合闸曲线，如图7-13所示。表7-5为合闸过程机械参数的对比。可以看到，新设计凸轮的平均合闸速度为1.18m/s，基本符合第3章得到的1.15m/s的优化合闸速度，误差仅为2.7%，并且新设计的凸轮能够有效地减小合闸弹跳幅值以及时间。使用该方法设计出来的凸轮能够将合闸弹簧的能量合理地分配在合闸的各个过程，有效减小合闸弹跳，并且在触头弹簧储能的过程中加大了输出的力矩，使得机构能轻松地克服触头弹簧的阻力，保证合闸的可靠性。

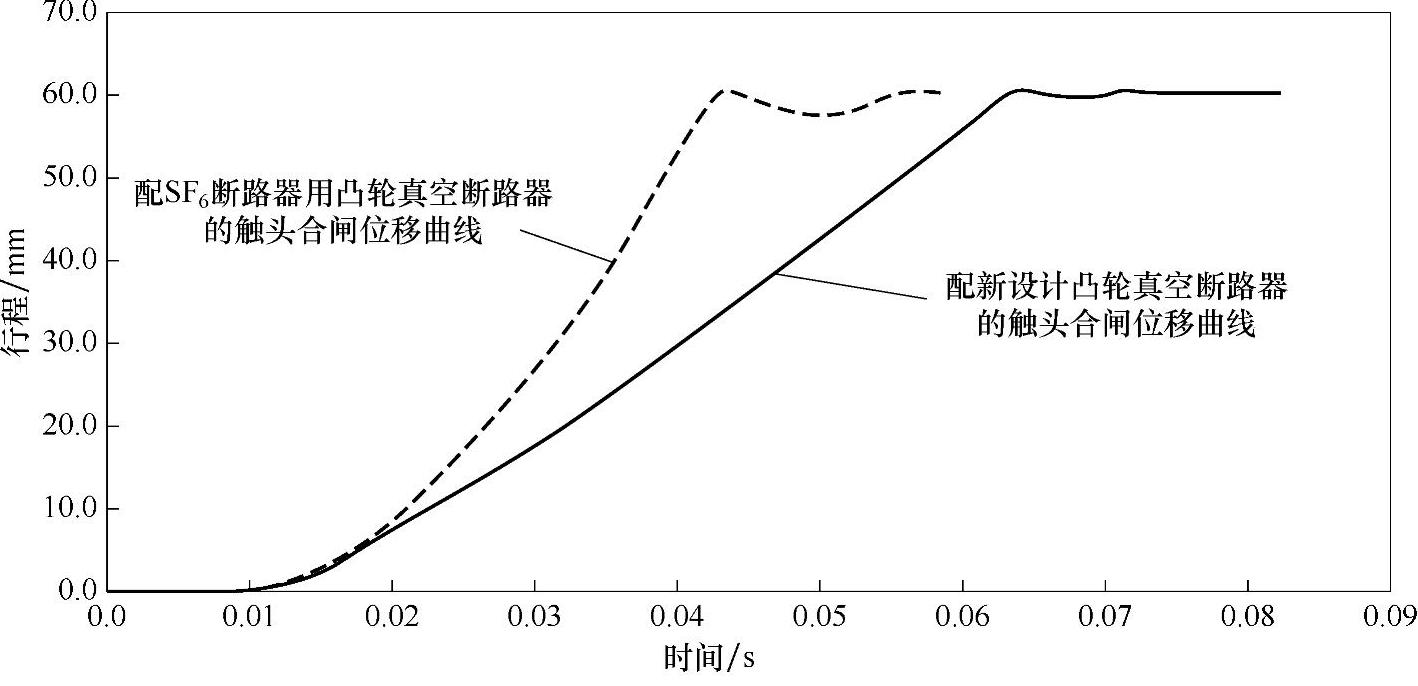
图7-13 两种不同凸轮的输出力矩曲线

表7-5 126kV真空断路器的归化质量