得到凸轮传动比的方法：通过合闸特性曲线

图7-8所示为一条典型的126kV真空断路器合闸特性曲线图。图中包括触头弹簧A、B两点的位移行程曲线。可以看到，当触头在闭合前，A、B两点以相同的特性运动，而触头闭合以后，A点将继续运动压缩触头弹簧直到机构走完合闸行程。因此，在高电压等级真空断路器的凸轮设计中，主要以A点的机构行程为设计依据，考虑在触头闭合前后的两种情况。

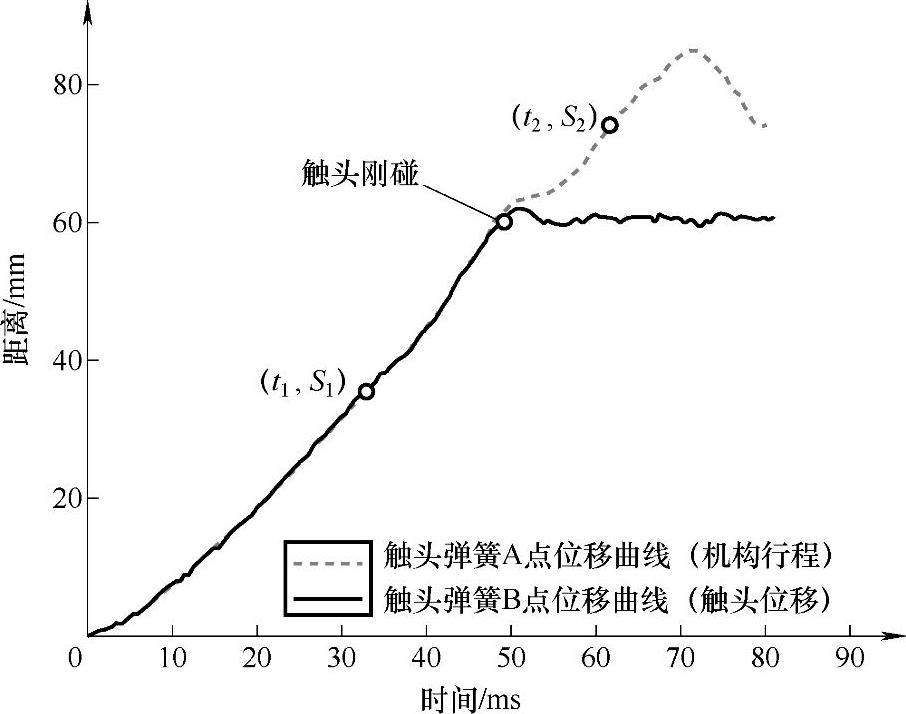
图7-8 典型的触头合闸特性曲线

由于绝缘拉杆以及一系列的传动杆件组成了一套曲柄滑块结构，而这种结构的传动比可以通过式（7-5）得到：

dH/dα=asinα+acosα（x₀-asinα）/b （7-5）

式中 H——滑块位移；

α——曲柄转角；

a——曲柄拐臂长度；

b——连接杆长度；

x₀——曲柄轴到滑块中线的距离。

当式（7-5）中a为内拐臂长度，b为绝缘拉杆长度，x₀为输出轴距离动触头中线的距离时，可以通过触头弹簧A点的位移H_ct计算出输出轴的转角α_s。

而此时刻的分闸弹簧运动距离也可以通过式（7-5）相同的形式计算出来，其中a为机构外拐臂长度，b为连接分闸弹簧的夹叉的长度，x₀为输出轴距离分闸弹簧中线的距离，可以通过输出轴的转角α_s得到分闸弹簧运动的距离H_f。因此我们将断路器所有的负载归一化到输出轴上，在输出轴转角α_s处对应的负载力矩可以通过式（7-6）得到：

T_f=F_fdH_f/dα_s+F_ctdH_ct/dα_s+T_m （7-6）

式中 T_f——在输出轴转角α_s处对应的负载力矩；

α_s——输出轴的转角；

F_f——在输出轴转角α_s处对应的分闸弹簧的力值；

H_f——在输出轴转角α_s处对应分闸弹簧的长度；

F_ct——在输出轴转角α_s处对应的触头弹簧的力值；

H_ct——在输出轴转角α_s处对应触头弹簧A点的位移；

T_m——该点摩擦力以及缓冲力产生的负载。

而此时负载消耗的总能量W_f为

另一方面，在输出轴转角α_s下，126kV真空断路器整机所获得的运动能量为

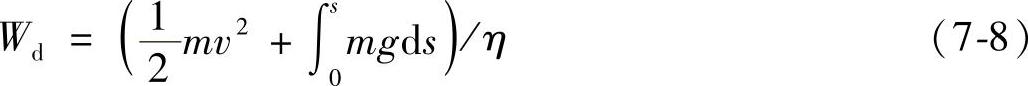
式中 m——在t时刻归化到触头弹簧A点上的质量；(www.xing528.com)

v——触头弹簧A点所具有的速度；

s——触头弹簧A点所对应的行程；

η——机构将能量由主轴传递给动触头过程中的效率因数。

由于在触头闭合前，触头弹簧没有作用，因此合闸弹簧的能量仅仅用于储存到分闸弹簧的能量以及动触头的能量上。

W_h=W_f+W_d （7-9）

而得到了合闸弹簧的能量通过式（7-10）就可以求得合闸弹簧的伸长量。

式中 H_h——在t时刻合闸弹簧的位移量；

H₀——合闸弹簧的原长；

W_h——在t时刻所需的合闸弹簧能量；

k——合闸弹簧的刚度系数。

储能轴与合闸弹簧也组成了一个曲柄滑块结构，仍然可以通过式（7-5）得到在t时刻储能轴的转角α_c。通过这种方法，在触头闭合前的所有时刻下，输出轴转角α_s与储能轴转角α_c都可以得到，从而能够得到一条理想的凸轮轮廓线。

该设计方法中，最关键的设计是在式（7-8）中归算质量m的计算。对于图7-7中的运动结构，126kV真空断路器的归算质量见表7-4。

表7-4 126kV真空断路器的归算质量

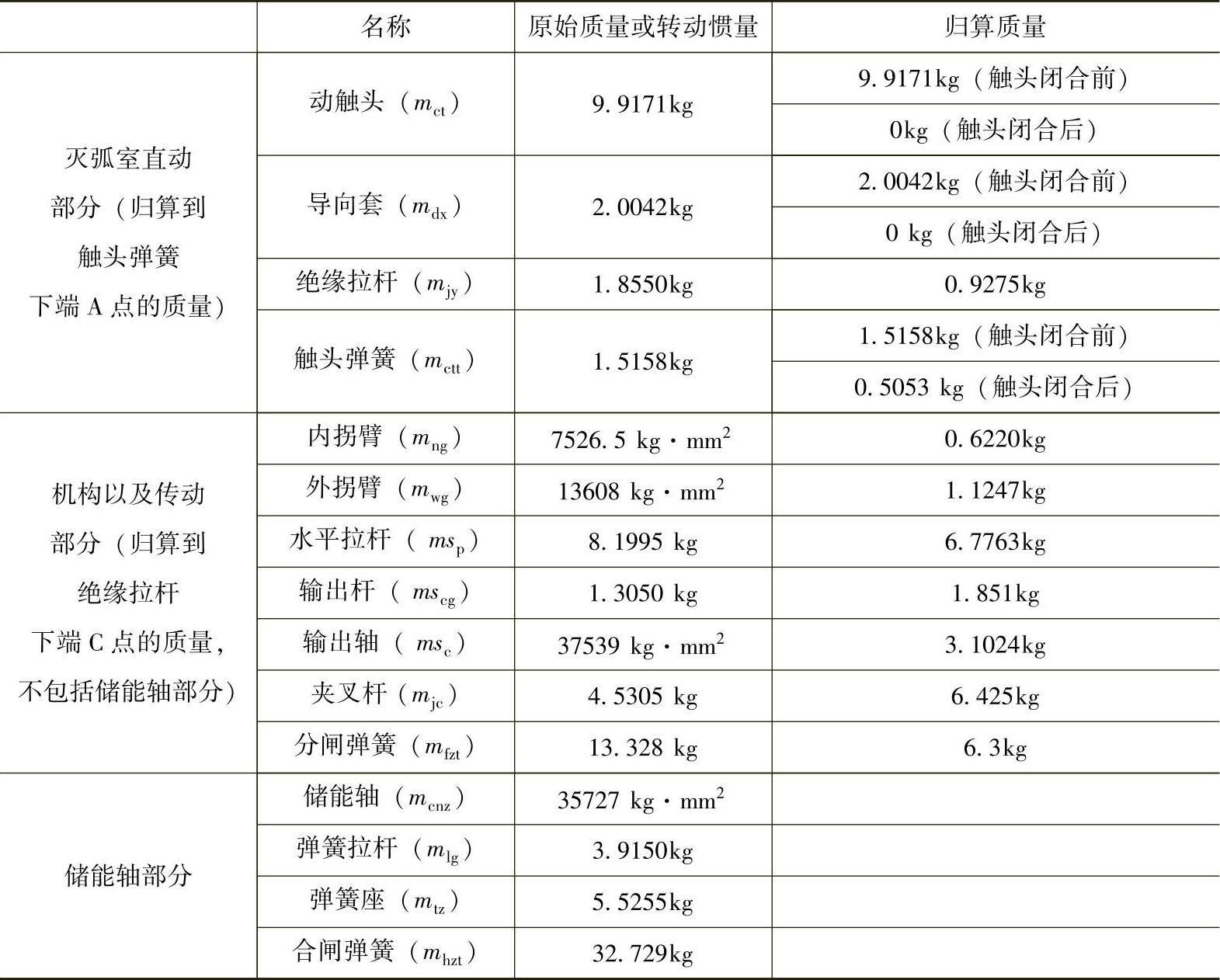
由于凸轮的轮廓在设计初期是不确定的，因此，储能轴部分的质量无法直接归算到触头弹簧的A点，因此无法直接计算出式（7-8）中动触头动能。

为了解决这个问题，我们通过数值迭代的算法，首先假定在触头转角α_s[i]处凸轮的传动比dα_s[i]/dα_c[i]，通过这个假定的传动比，可以根据输出轴角度为α_s[i]时储能轴的角度α_c[i]以及合闸弹簧的位移H_hz[i]，根据式（7-10）可以得到合闸弹簧的能量W_h[i]，通过合闸弹簧的能量减去该时刻的负载能量H_f[i]，就可以得到触头获得的能量W_d[i]。另一方面，利用设定的传动比可以将储能轴部分归算到A点的质量，从而计算出126kV真空断路器在A点总的等效质量m[i]，通过式（7-11）可以计算出在该假定的传动比下得到的一个合闸速度v_temp[i]：

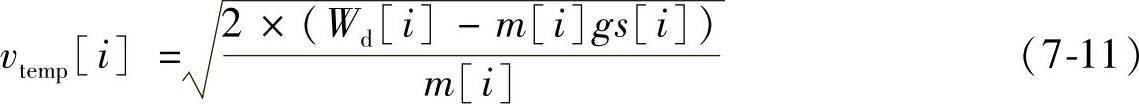
式中 v_temp[i]——在假定传动比下输出轴转角为α_s[i]时的合闸速度；

m[i]——在假定传动比下输出轴转角为α_s[i]时归算到A点的等效质量；

W_d[i]——在假定传动比下输出轴转角为α_s[i]时传递到A点的能量；

s[i]——α_s[i]处对应的A点的位移。

将此时由能量计算出的v_temp[i]与目标合闸行程-时间曲线中计算出的合闸速度v[i]进行比较。当v[i]-v_temp[i]＜ε时，可以认为此时假设的传动比dα_s[i]/dα_c[i]符合要求；若v[i]-v_temp[i]＞ε时，则dα_s[i]/dα_c[i]=dα_s[i]/dα_c[i]+Δ（dα_s/dα_c），重复上面的迭代过程，直至符合要求为止。

至此可以将输出轴转角为α_s[i]时的传动比计算出来，而储能轴转角α_c[i]也能够确定。将α_s[i]从分闸位置的角度转到合闸终了的角度过程中，由每个时刻的储能轴转角α_c[i]从而可以得到一条输出轴转角与储能轴转角及传动比的关系式。