关合电流对预击穿和弹跳燃弧时间的影响

本节的实验结果都是基于没有电流流过时的机械弹跳得到的数据。在实际电路中，预击穿电弧和弹跳电弧均可以流过主回路电流，往往能达到几十千安。在这种情况下，回路电流产生的作用就变得不可忽略。

对带载触头合闸运动很重要的因素是电动力。Barkan指出，即使触头在无载关合情况下，触头没有弹跳出现，但是通过测量触头间的动态压力发现，触头合闸的保持力在许多时间段非常低，如果电流引起的电动斥力大于这些低的保持力时，将会形成新的弹跳。另外，电动斥力将会阻碍触头的关合运动，从而增加了触头弹开的时间。下述关系式是Holm提出的电动斥力公式：

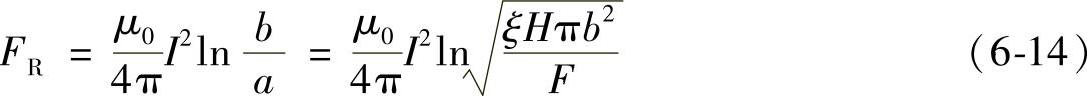
式中 F_R——接触处产生的电动斥力（N）；

μ₀——真空的磁导率（H/m）；

I——通过触头的电流（A）；

b——圆柱形触头的半径（mm）；

a——接触点的半径（mm）；

ξ——与接触面状况相关的系数，其范围在0.3～1之间；

H——材料的布氏硬度（N/mm²）；

F——接触力（N）。

对于本节所研究的126kV真空灭弧室触头，短路电流为40kA，触头材料为CuCr50，硬度为90N/mm²，ξ取最大值1，动触头半径为50mm，触头在刚碰时触头压力为5500N，可以计算出触头刚碰时受到的最大电动斥力约为388.5N。

在126kV真空断路器中，由于灭弧室触头是纵向磁场结构，在发生预击穿情况下，短路电流通过线圈时产生的磁场力也会对触头的运动速度产生影响，图6-12所示的126kV真空断路器触头线圈结构为2/3匝线圈。通过40kA短路电流时，这两个线圈可以等效为两个圆环，圆环之间的距离由开距、线圈厚度以及触头片厚度组成，通过每个线圈的电流为26.67kA。根据电磁力计算关系可得，该两圆环之间的电动吸力的大小为

(www.xing528.com)

式中 F_A——电动吸力（N）；

μ₀——真空中的磁导率（H/m）；

I——线圈通过的电流（A）；

R——线圈的外径（m）；

r——线圈的内径（m）；

D——线圈的间距（m）。

其中，线圈外径为50mm，内径为35mm，线圈的间距D由触头片厚度（6mm），线圈厚度（22mm）以及触头开距组成。当灭弧室在开距为4mm处发生预击穿，短路电流40kA下通过触头时，线圈产生的电动吸力为1000N。电动吸力随着开距的减小逐渐增大，在触头接触时电动吸力增加到1117N。因此，考虑电动吸力与电动斥力的合力，带载情况下合闸速度将会提高，合闸后的弹跳会对本节中图6-8以及图6-9中的数据会产生一定的影响。

在预击穿阶段，预击穿电弧的产生远远比我们假设的复杂。Kharin等人发现预击穿电弧需要由稳定燃烧的阴极斑点来维持。而在预击穿过程中很多击穿现象都不能够形成预击穿电弧。Slade还提出，真空断路器在操作很多次以后，触头表面会发生变化，从而导致预击穿开距的增加。因此，预击穿开距以及预击穿电弧的持续时间很难在带载情况下确定。

另外，如果预击穿电弧在触头闭合前产生，一方面，燃弧过程中产生的蒸气压会造成触头震动以及触头电动斥力，从而增加预击穿时间；另一方面，由于电弧会加热触头表面使得触头变软，因此在碰撞过程中触头表面将吸收更多多余的动能，因此会减小触头弹跳的时间。

我们还对126kV真空断路器进行了全电压关合对称短路电流试验。图6-13所示为126kV真空断路器试验中通过40kA断路电流合闸曲线与空载合闸曲线的比较。从图中可以看到，触头的运动特性与空载情况区别不明显。但是由于全电压关合试验仅仅在其中一相进行试验，短路电流对断路器负载产生的影响都不显著，因此有载情况下的优化合闸曲线需要进一步的研究。但是，126kV真空断路器样机在试验后能够正常分合闸操作，说明在该设计的合闸特性下，动熔焊没有导致分闸失败。因此从无载关合操作推导出的优化的合闸特性仍然具有非常重要的意义，它能够给配合126kV真空断路器动熔焊特性的机械特性设计提供参考，从而指导真空断路器操动机构的设计。

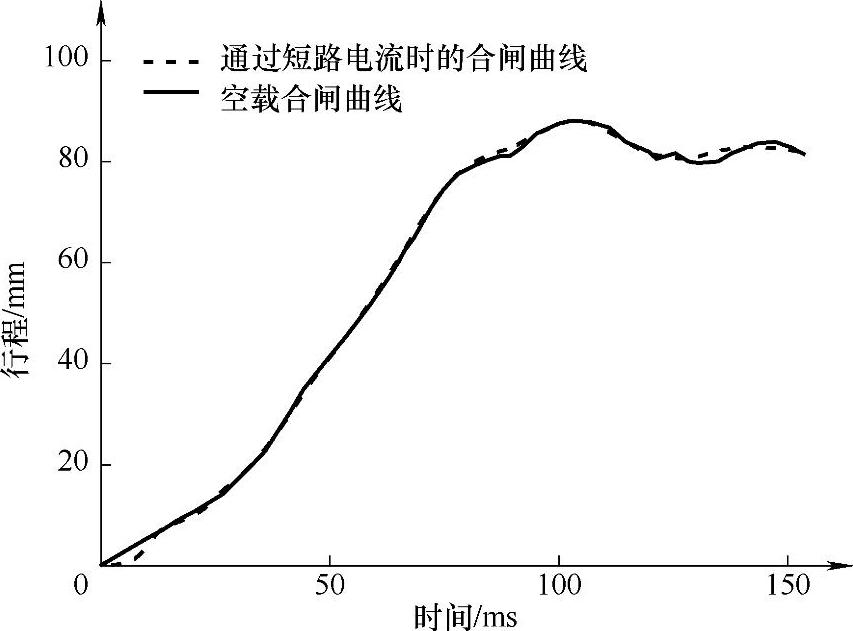
图6-13 126kV真空断路器全电压关合试验合闸曲线与空载合闸曲线