优化PIC方法计算等离子体中的近碰撞效应

经典和相对论力学都使用力或者力场来描述物质间的相互作用。对于等离子体来说，带正电的离子和负电的电子之间的相互作用是通过电场和磁场来实现的。这样如果我们知道粒子p的电荷q_p、位置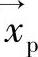、速度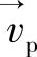，通过计算电场和磁场在位置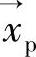的值，就可以获得施加到粒子p的电场力和洛伦兹力为

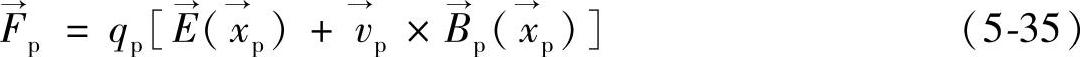
电场和磁场由等离子体本身以及等离子体外部的源产生，可以通过求解麦克斯韦方程获得。这样看来似乎等离子体问题的求解并不存在特别的困难，只要知道等离子体中每个带电粒子的初始位置，由式（5-35）决定的运动控制方程和麦克斯韦方程就可以确定带电粒子的运动规律，进而可以通过预测粒子的运动得到等离子体的宏观规律。

但是等离子体由大量带电粒子组成并且数量庞大，通过预测每一个带电粒子的运动规律获得等离子体的宏观特性在理论上存在可能，实际却面临无法解决的问题，粒子的数目已经远远超过了现阶段计算机的计算能力。采用这种方法计算等离子体，无法在一个有效的时间内获得结果。为了解决这个问题，超粒子的概念被引入等离子体模拟计算中。所谓超粒子就是用一个粒子来描述等离子体分布函数相空间中的一点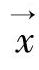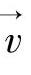（，）周围的所有粒子。因为这点附近的粒子对等离子体中的其他粒子的作用力以及电磁场的贡献基本相同，由式（5-35）可知这些粒子的运动规律也基本相同，所以不需要跟踪此点附近的所有粒子，只需要计算一个粒子的运动特性就可以代表相空间中一点附近所有粒子的特性。这种特性与德拜长度所表征的等离子屏蔽效应是一致的。这样，超粒子的引入使得计算机处理包含大量带电粒子的等离子体的计算成为可能。

虽然超粒子的引入使得计算成为可能，但是依然存在一个严重的问题，阻碍了模型的进一步推广。因为超粒子被处理成为一个点电荷，当两个超粒子距离较远时，点电荷之间的相互作用力符合库仑定律，为库仑力。但是如果两个超粒子的距离逐渐靠近的话，因为超粒子被处理成为点电荷，所以按照库仑定律力会逐渐趋于无穷，这与实际是不相符合的。事实上这个效应是因为将分布在空间中数量众多的带电粒子处理成仅为空间一点的超粒子所带来的近碰撞效应。当两团等离子体相互重合时，它们之间的库仑力会逐渐减小，直至完全重合归为零。超粒子的引入带来了近碰撞效应，从根本上扭曲了等离子体集体运动特性，也不能适应等离子体模拟的要求。

为了解决近碰撞效应的问题，Birdsall等人提出了有限大小粒子。如图5-37所示，当距离较远时有限大小粒子表现出点电荷的特性；而当两个有限大小的粒子靠近时，则作用力逐渐减小直到降为零。有限大小粒子的方法可以有效降低近碰撞效应所带来的影响，最大限度的保留下等离子体集体运动的特性。

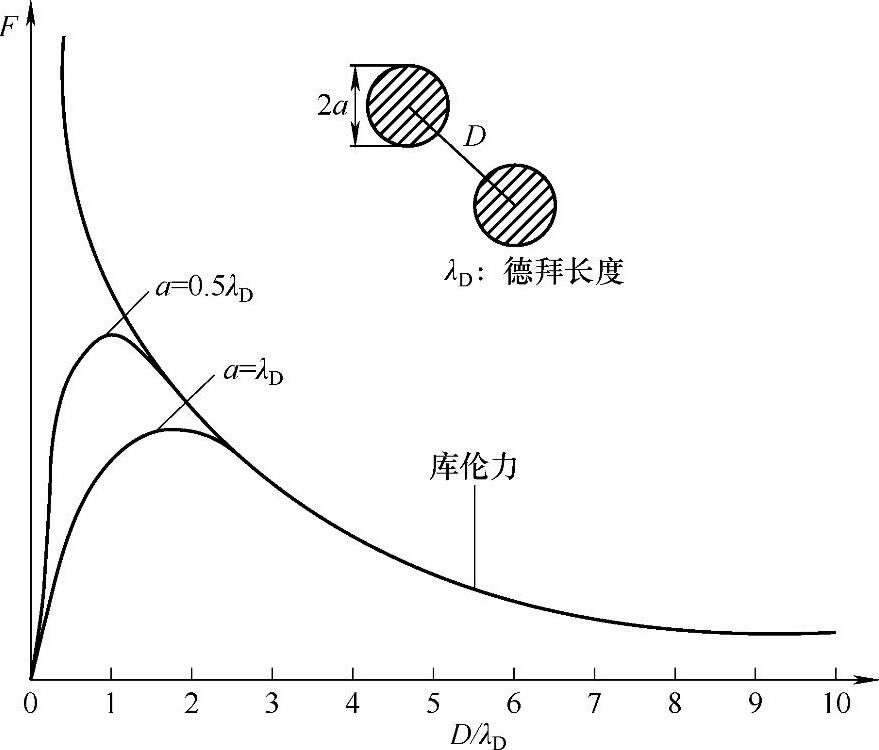
图5-37 有限粒子之间的相互作用

为了进一步说明PIC方法，结合本书所研究的弧后鞘层问题，考虑一个一维静电场等离子体问题。等离子中的电子和离子的相空间分布函数为f_s（x，v，t），代表一个相空间中某个相点（x，v）附近dxdv范围内可能发现的粒子数目，其中s代表不同的带电粒子。其中等离子体的控制方程为Vlasov方程，可以表示为

式中 q_s——粒子电荷量（C）；

m_s——粒子质量（kg）。

分布函数f_s（x，v，t）是一个连续的表达式，计算机处理时需要对其进行离散和截断。PIC方法认为相空间中的分布函数可以由若干个单元的分布函数组成f_p（x，v，t），每一个单元都代表了相空间中某点附近的大量粒子，也就是上面提到过的有限大小粒子。可以表示为

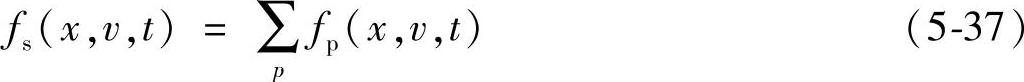
PIC方法还需要给每一个有限大小粒子的分布函数指定型函数，以确定其中的分布状态。通常相空间中每一维都有一个型函数去构造其分布函数，对于我们的问题，可以表示为

f_p（x，v，t）=N_pS_x（x-x_p（t））S_v（v-v_p（t）） （5-38）

式中 N_p——一个有限大小粒子中的粒子数量；(www.xing528.com)

x_p——有限大小粒子在相空间中的坐标位置（m）；

v_p——有限大小粒子在相空间中的速度位置（m/s）；

S_x——坐标空间的型函数；

S_v——速度空间的型函数。

对于型函数S必须满足归一化条件，即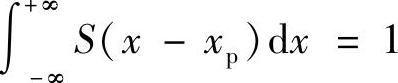，并且应该令S（x）≠0的范围足够小，且S（x）=S（-x）。满足这些条件的函数非常多，通常使用多项式的样条插值来实现。

将式（5-37）和式（5-38）代入式（5-36）并且在速度空间和坐标空间积分，可以得到完整的Vlasov演化方程为

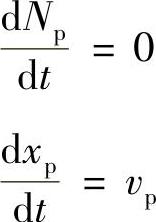
式中 E_p=∫S_x（x-x_p）E（x）dx。

根据分布函数为f_s（x，v，t）的定义式（5-37）以及式（5-38），空间中的粒子电荷密度分布可以表示为

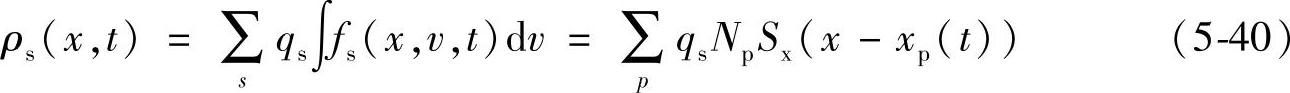
在静电模型中认为粒子的运动主要由静电场决定，可以忽略感应电磁场，因此只需要求解Possion方程。静电模型适用于包括等离子体鞘层问题在内的一类特征时间较长的问题。这样电势可以表示为

式中 ρ——粒子电荷密度（C/m³）；

ε₀——真空中介电常数（F/m）。

这样式（5-39）～式（5-41）就构成了PIC计算的完整方程组，可以求解Vlasov-Maxwell系统所确定的等离子体问题。