非均匀场击穿模型探究

在上节均匀场击穿模型的基础上，进一步建立非均匀场中的击穿模型。微粒击穿的物理过程与均匀场中类似，如图2-16所示。

在非均匀场中，电场强度E与真空间施加的电压U之间的关系为

式中 β——场致增强系数。

场致增强系数包括微观场致增强系数β_m和宏观场致增强系数β_g。本节假设微观场致增强系数为常数，所以主要讨论宏观场致增强系数，即几何场致增强系数β_g。因为假设引起击穿的微粒位于电场强度最强的地方，所以击穿场强表示为

式中 β_max——宏观场致增强系数的最大值。

由于不同的灭弧室与触头结构空间电场分布不同，场致增强系数也不同。本实验采用的触头模型，触头直径为60mm，触头边缘倒角为6mm，可以通过仿真得到不同触头间隙距离下触头间的电场分布，进而得到不同触头间隙距离下宏观场致增强系数。图2-17是开距为50mm时的宏观场致增强系数的典型分布图。

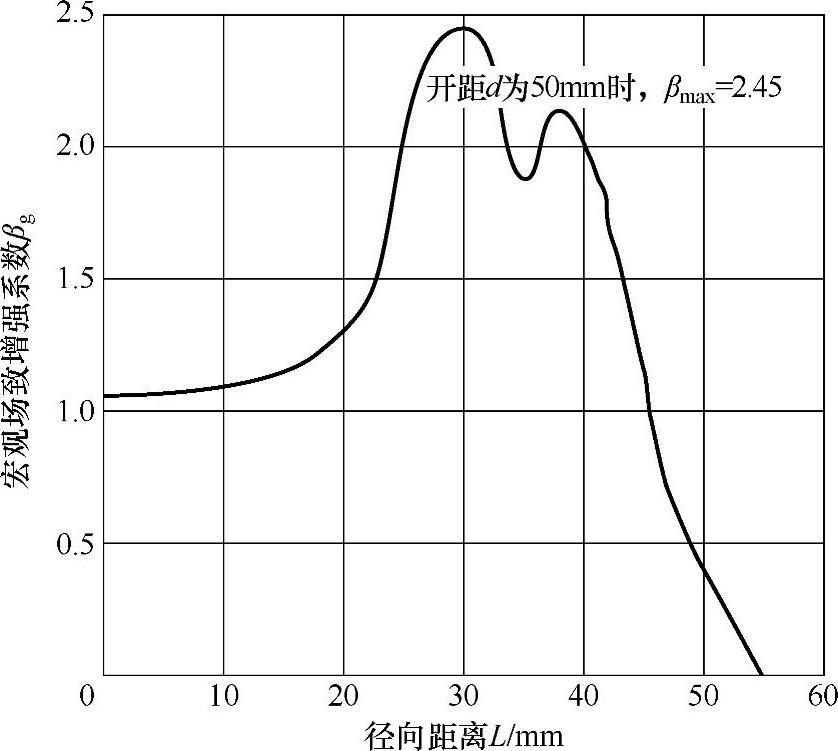
图2-17 开距为50mm时的宏观场致增强系数的典型分布图

将数值仿真获得的不同触头间隙距离下的宏观场致增强系数的最大值β_max与触头间隙距离d之间关系进行线性拟合可以得到

β_max=0.3017d^0.5435 （2-32）

将式（2-32）代入式（2-31）可以得到

将式（2-33）代入式（2-21），则可以得到非均匀场下真空间隙击穿时的临界击穿电压为

U_c=C₄d^0.2283 （2-34）

式中 C₄=1.82C₃。

在此基础上对冲击电压作用下的微粒击穿过程进行分析，波头的电压上升速率为定值α，假设击穿发生在波头，即冲击电压的上升沿，微粒开始运动的时刻遵循Cranberg的微粒击穿的假设，即认为达到Cranberg定义的临界值时，微粒脱离母体电极向对面电极移动。

首先微粒在真空间隙飞行过程中受力满足

式中 m_p——微粒质量；

t——微粒脱离母体电极后的时间；

x（t）——t时刻，微粒离开母体触头的距离；

U（t）——t时刻电压瞬时值；

Q_p——微粒所带电量；

d——触头间隙距离。

假设冲击电压是匀速上升的，且上升率为α，则瞬时电压U（t）可表示为

U（t）=U_c+αt （2-36）

式中 U_c——击穿的临界值。(www.xing528.com)

将式（2-36）代入式（2-35）得到

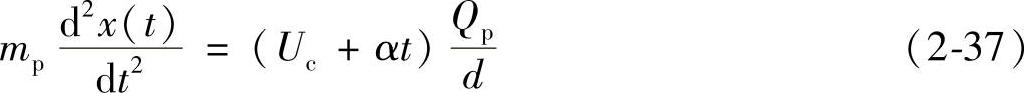
式（2-35）满足初始条件，x（0）=0，x（t_d）=d，，对两边进行积分得到

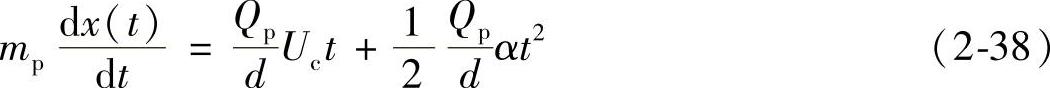
对上式两边再次积分得到

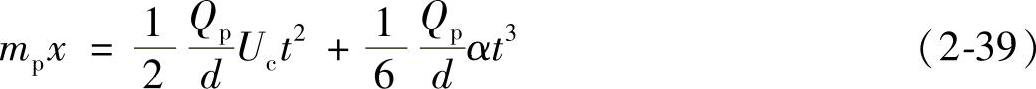
当x=d时，，其中U_b为击穿时刻的瞬时电压值，代入式（2-38）得

将式（2-40）进行化简得

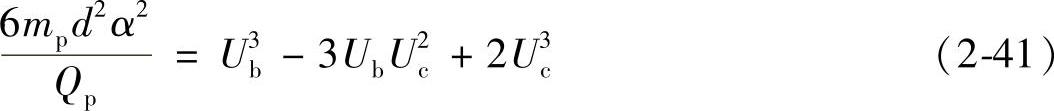
式中

所以Q_p满足

将式（2-42）～式（2-45）代入式（2-41）得

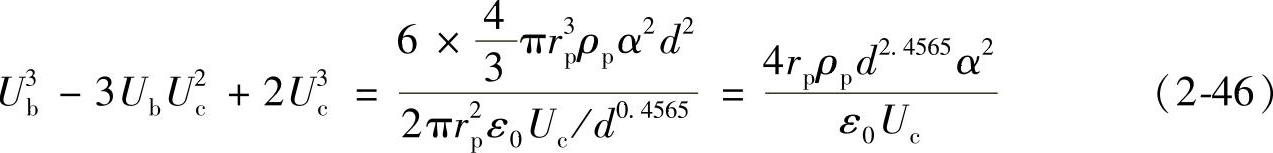
根据卡丹尔求解公式x³+px+q=0，其实数解为

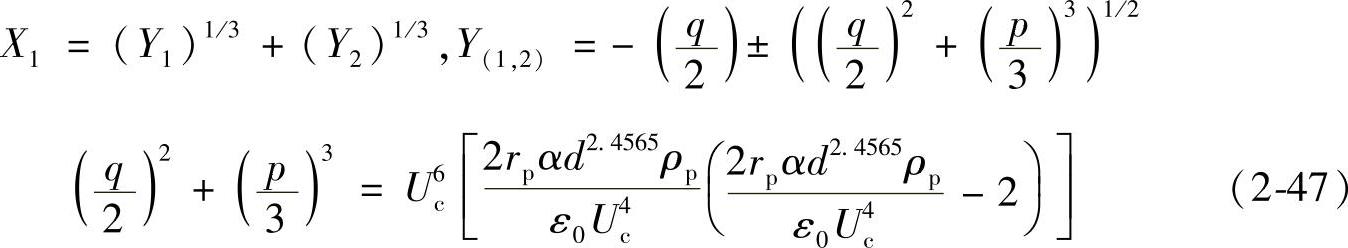
对于ε₀=8.85×10^-12F/m，α≈100kV/1.2μs，ρ_p=8.9×10³kg/m³，U_c≈100kV，r_p≈10μm，则，则可以对式（2-47）简化得到高电压等级真空灭弧室在冲击电压作用下非均匀场中击穿电压与触头间隙距离之间的满足下式：

式中 C₃——与触头形状、电场分布、触头材料以及微粒尺寸等有关的定值。

以本章大量实验数据为基础，对本模型进行了对比分析，比较结果如图2-18所示。从图中可以看到，冲击电压作用下非均匀场中的击穿模型与实验结果较为吻合，而击穿电压在一定程度上可以反映击穿过程，说明该真空灭弧室在冲击电压作用下非均匀场中的击穿模型具有一定的合理性。

图2-18 实验结果与理论模型对比图

以上基于Cranberg的真空间隙微粒击穿理论（均匀场、直流电压下），提出了高电压等级真空灭弧室击穿过程的物理模型（非均匀场，雷电冲击电压下），并与实验结果进行了比较，所得到的结论如下：

1）基于Cranberg的微粒击穿理论，建立了真空间隙在冲击电压作用下均匀场中击穿过程的物理模型，得到了电压U_B与触头间隙距离d之间的关系满足U_B∝d^0.8。

2）基于以上击穿模型，建立了高电压等级真空灭弧室在冲击电压作用下非均匀场中的真空击穿的物理模型，得到了击穿电压U_B与触头间隙距离d之间的关系为U_B∝d^0.74；

3）通过冲击击穿实验得到了高电压等级真空灭弧室在非均匀场中击穿电压U_B与触头间隙距离d之间的关系为：U₅₀∝d^α，其中α为0.70～0.79。而对于所建立的冲击电压作用下非均匀场中的物理模型，其击穿电压U_B与触头间隙距离d之间关系为：U_B∝d^0.74，这一结果证明了所建立的物理模型的正确性。