触头有效面积对性能的影响

触头有效面积区域指触头表面上更容易发生击穿的区域，触头有效面积的定义为电场强度不小于90%最高电场强度的触头表面面积。对于输电等级真空灭弧室而言，触头有效面积对真空灭弧室绝缘强度的影响比较复杂，因为触头间隙距离较大且触头尺寸较大，所以触头间的电场分布会随着触头间隙距离的变化而发生变化。在小触头间隙距离下，触头间电场分布相对比较均匀，但是较大间隙距离下则为非均匀场。另外，随着触头间隙距离的增加屏蔽筒等部件对触头间的电场分布将会产生重要的影响，而这个影响在中压灭弧室中几乎可以忽略。所以，此前这方面研究不足，无法为输电等级真空灭弧室的设计提供有价值的参考。

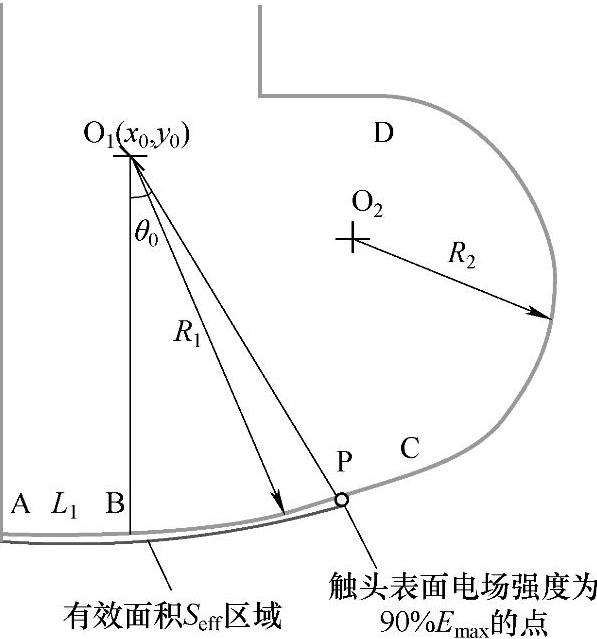
图2-10 有效面积计算示意图

1.触头有效面积计算

计算模型真空灭弧室的触头有效面积时，首先要对电场分布进行仿真计算，然后求取电场强度不小于90%部分的面积。有效面积的计算示意图如图2-10所示。如果触头表面上电场强度为90%最大电场强度的点为P点，则S_eff表明的区域为有效面积区域，BC弧段的圆心坐标为O₁（x₀，y₀），BO₁和PO₁的夹角为θ₀。当已知电场分布时，由图2-10可以计算出触头的有效面积为

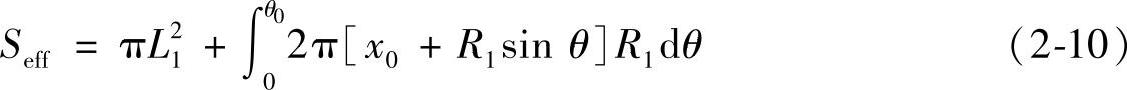
式中 L₁——直线部分的长度；

x₀——BC弧段的圆心x轴坐标；

R₁——BC弧段的半径；

θ₀——BC弧段上有效面积区域的起始位置的夹角。

2.雷电冲击耐压实验

实验采用±1800kV标准雷电冲击电压发生器，产生标准雷电脉冲电压（1.2/50μs），对真空灭弧室进行标准雷电冲击电压的耐压实验。通过升降法获得具有一定绝缘耐受概率的绝缘耐压值。

Weibull分布函数被广泛应用于真空间隙击穿电压的统计分析中，其通常有两种形式，即二参数Weibull分布函数和三参数Weibull分布函数。

其中二参数Weibull分布函数是假设下限为零，即当击穿电压的累计概率为零时击穿电压为零。二参数Weibull概率函数的形式如下：

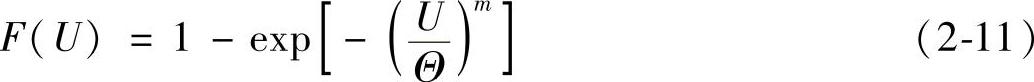
式中 F（U）——电压为U时的累计击穿概率；

m——Weibull函数的形状因子；

Θ——尺度参数。

三参数Weibull分布是指当下限不为零时，即当击穿电压的累计概率为零时，而击穿电压不是零。三参数Weibull概率函数的形式如下：

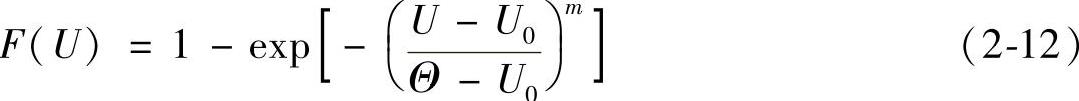
式中 F（U）——电压为U时的累计击穿概率；

U₀——累计击穿概率为0时的击穿电压值；

m——Weibull函数的形状因子；

Θ——尺度参数。

在图2-11中，横坐标表示电压U，纵坐标表示累积击穿概率F（U）。对图2-11中不同有效面积下的累积击穿概率曲线用三参数的Weibull函数进行拟合，拟合结果见表2-1。其中R-square用于表示拟合度，不同有效面积下累积击穿概率的Weibull函数的拟合度都很高。如表2-1所示R-square均大于0.9，所以假设不同有效面积下的概率分布符合三参数Weibull函数式是合理的。另外，通过表2-1还可以看出，随着有效面积的增加，U₀会下降。

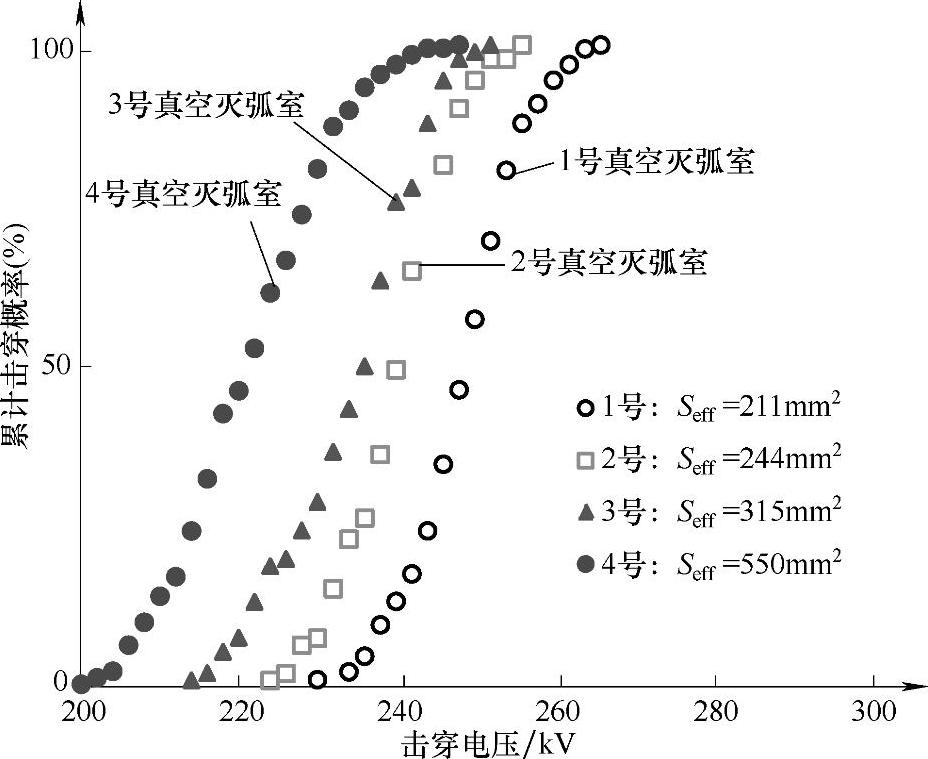
图2-11 不同有效面积下击穿电压的累积击穿概率分布

表2-1 不同有效面积下的累积击穿概率三参数拟合结果

(www.xing528.com)

由此可见，在真空中当触头间隙的电场为均匀场时，其击穿电压的概率分布均符合Weibull分布，而且Weibull分布的形状因子不随有效面积的变化而变化。

3.大开距条件下触头倒角影响

实验研究中设计了两只触头轮廓不同的高电压等级（126kV）真空灭弧室，以此获得不同触头有效面积，以研究非均匀场下不同触头有效面积对雷电冲击绝缘特性的影响。实验中所用的模型真空灭弧室结构与前一节实验研究的结构相似，主要是触头结构和开距有所不同。为了在相同触头间隙距离下获得不同的触头有效面积，两只真空灭弧室触头边沿的倒角分别为R=6mm和R=2mm。通过升降法得到真空灭弧室在不同触头间隙距离下，标准雷电冲击击穿电压的实验记录，触头间隙距离范围为10～50mm。

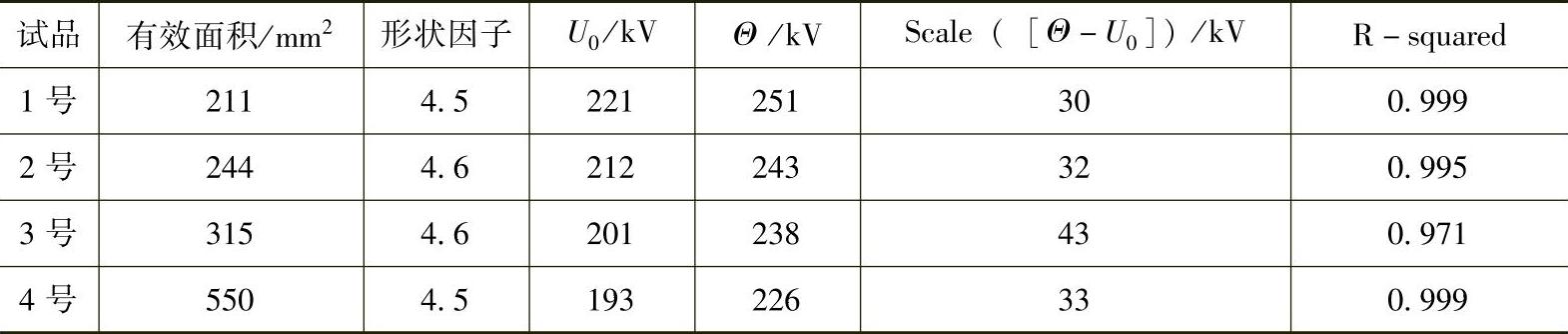
图2-12所示为两只触头倒角不同的试品在不同触头间隙距离下击穿概率为50%的击穿电压U₅₀。对相关数据进行拟合，分别得到的关系为

U₅₀=30×d^0.70 （R=6mm） （2-13）

U₅₀=40×d^0.65 （R=2mm） （2-14）

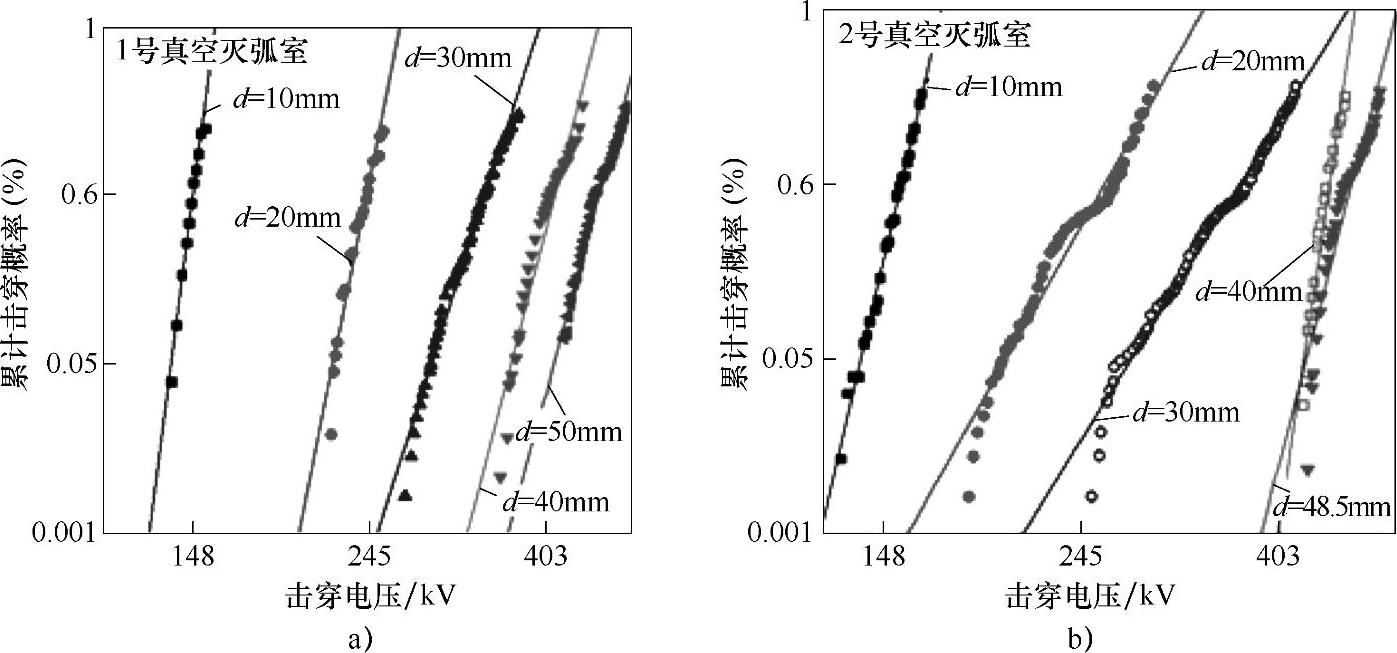
图2-12 不同触头倒角真空灭弧室的击穿电压概率分布曲线图

a）触头边沿倒角为R=6mm真空灭弧室 b）触头边沿倒角为R=2mm真空灭弧室

在得到两只不同触头轮廓的高电压等级真空灭弧室的击穿电压后，为了对比触头有效面积对击穿电压的影响，分别计算两只真空灭弧室在不同触头间隙下的触头有效面积。有效面积的计算程序如前节所示，即先仿真计算电场强度分布，获得触头表面最大电场强度和最大电场强度的分布区域，然后积分计算电场强度大于90%最大电场强度的面积，最后获得有效面积。通过以上的仿真和计算，可以得到不同倒角触头的真空灭弧室在不同触头间距下的有效面积S_eff、触头表面最大场强E_m。又因为宏观场致增强系数满足公式：

即可得到不同触头间距下的有效面积S_eff、触头表面最大场强E_m以及宏观场致增强系数β_g之间的关系。

图2-13所示为两种倒角真空灭弧室的击穿电压比较。由图中可知，在不同间隙距离下，触头倒角为R=2mm的真空灭弧室其击穿电压高于倒角为R=6mm的真空灭弧室。这一结果可以通过有效面积对微观场致增强系数、宏观场致增强系数的影响来解释。

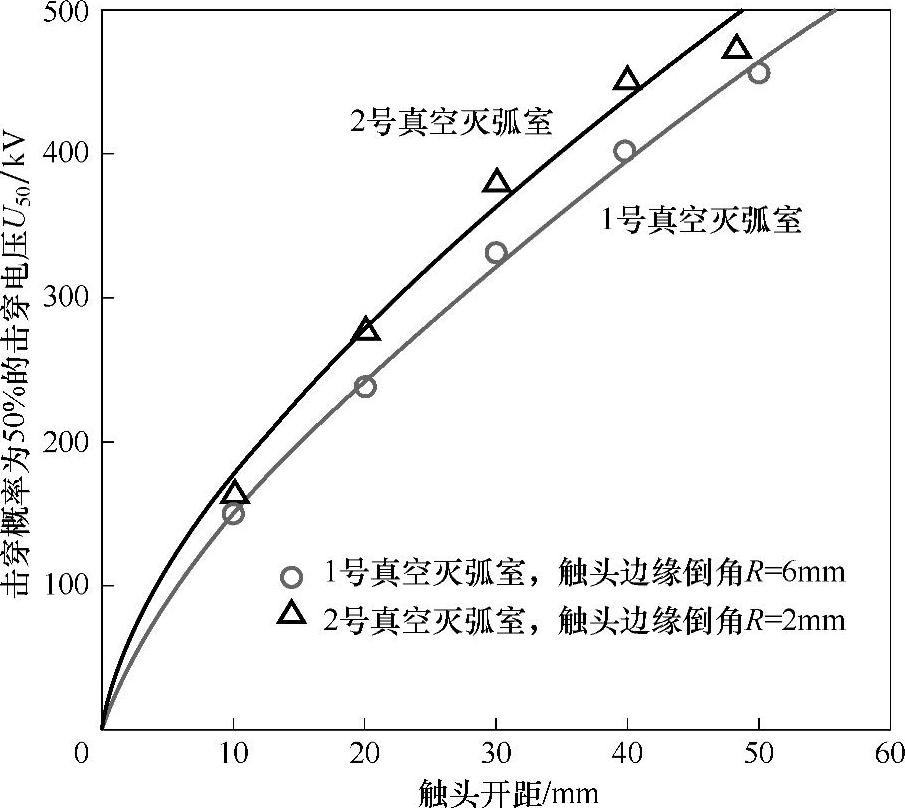
图2-13 不同触头倒角灭弧室击穿电压的比较

首先微观场致增强系数β_m与触头有效面积S_eff之间存在着如下的经验公式：

β_m=C₁S^α_eff （2-16）

式中 C₁、α——常数，且α约为0.26。

又因为击穿电场场强E_B满足关系式：

则可以得到击穿电场场强E_B与触头有效面积S_eff之间的关系满足关系式：

仿真计算表明，倒角R=2mm的真空灭弧室其S^α_effβ_g高于倒角R=6mm的真空灭弧室，又因为S^α_effβ_g正比于击穿场强E_B，故倒角R=2mm的真空灭弧室击穿电压高于倒角R=6mm的真空灭弧室，这一点与实验结果相一致。

通过对真实灭弧室为对象的实验研究，发现输电等级真空灭弧室在均匀场和非均匀场中触头有效面积对真空灭弧室绝缘特性的影响如下：

1）在触头间隙距离6mm下均匀场中，击穿概率为50%的击穿电压U₅₀与有效面积S_eff的关系满足：U₅₀∝S^-0.12_eff。该发现不同于以前的真空绝缘理论中关于有效面积的认识。

2）在触头间隙距离10～50mm的非均匀场中，有效面积从宏观效应和微观效应两方面影响真空灭弧室。实验发现，通过减小有效面积，可以在一定程度上提高击穿电压。

3）本实验使用的真空灭弧室模型获得的50%击穿电压U₅₀与触头间隙距离的关系满足U₅₀=kd^α，其中k为常数，幂指数α在0.6～0.7范围内。