工频击穿场强分析方法优化

1.工频击穿场强的基本关系

真空间隙在电压U作用下其触头间隙的电场分布是非均匀的，分别定义微观场致增强系数β_m和宏观场致增强系数β_g，表示局部电场由于微观结构和宏观结构的影响，使得局部电场强度增强的程度。由此，在电压U的作用下，触头间距为d的真空间隙中的最大电场强度E_m为

式中 β_m——微观场致增强系数；

β_g——宏观场致增强系数。

假设触头间隙发生击穿时，击穿位置在触头表面电场强度最强处，若此时触头间隙施加的电压为U_B，则触头间距为d时触头间隙的击穿场强E_B可表示为

通过对可拆真空灭弧室中一对平板电极的击穿电压与触头间隙距离的关系研究发现，其击穿电压与触头间隙距离的关系满足

U_B（d）=K₁d^α （2-7）

式中 K₁、α——常数。

将式（2-7）代入式（2-6）中，可以得到不同触头间隙距离下击穿场强应满足下面的公式：

E_B=β_mβ_gK₁d^（α-1） （2-8）

由此可知，这样定义的击穿场强会随着触头间隙距离以及电场分布的不同而发生变化。

以图2-5a的触头形状为例，计算分析击穿场强与触头间隙距离之间的关系。其中触头直径为30mm的平板电极，触头厚度为10mm，导角半径为2mm。通过电场仿真数值计算可以得到在不同触头间隙距离下，沿触头表面分布的宏观场致增强系数β_g，如图2-5b所示。

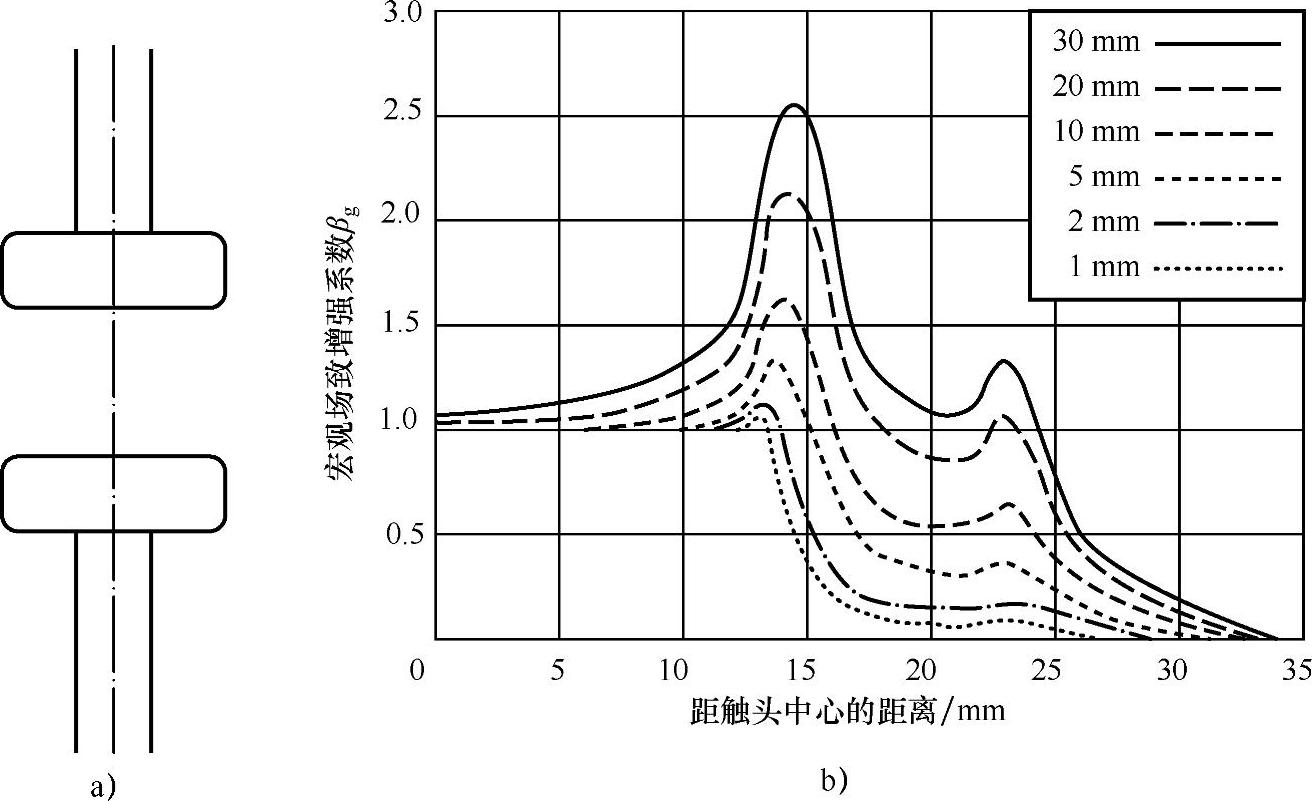
图2-5 宏观场致增强系数β_g的分布

a）真空中的平板电极 b）宏观场致增强系数β_g沿触头表面的分布

假设真空间隙的击穿发生在电场强度最强的地方，即发生在最大宏观场致增强系数β_gmax处，且假设不同触头间隙距离下微观场致增强系数β_m为常数。且由图2-5b可知，当触头间隙距离为1mm时β_gmax（1）≈1。由式（2-5）可以得到不同触头间隙距离下的击穿场强与1mm触头间隙距离时的击穿场强之比满足下面的关系式：(www.xing528.com)

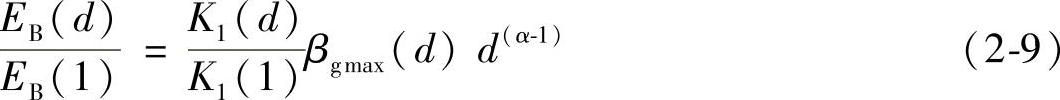
假设对于形状如图2-5a所示平板触头，当触头间隙距离在0～30mm范围内时，击穿电压U_B与触头间隙距离之间的关系满足：U_B∝d^0.5，综合图2-5b所示不同触头间隙距离下的最大宏观场致增强系数β_gmax，则可以得到图2-5a所示电极在不同触头间隙距离下的击穿场强与1mm触头间隙距离时的击穿场强之间的关系如图2-6所示。

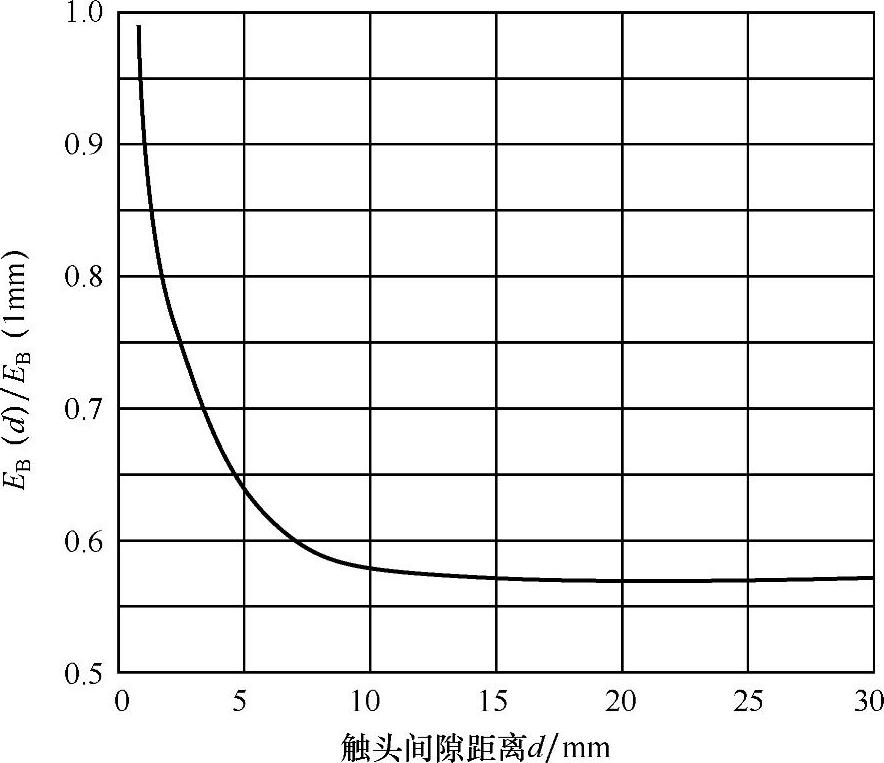
图2-6 在不同触头间隙距离下的击穿场强与1mm触头间隙距离时的击穿场强之比

以上分析建立了真空中平板电极击穿场强与触头间隙距离的基本关系模型，但是对于长间隙真空灭弧室（触头间隙距离60mm）来说，还应进一步考虑屏蔽罩的影响，需要分析交流工频电压的情况，并且通过实验验证。以下将进一步分析长间隙工频绝缘特性，获得长真空间隙工频电压击穿场强与触头间隙距离的关系，为输电等级真空灭弧室工频绝缘特性的设计提供理论依据。

2.长间隙工频击穿场强的计算

与上节中的分析思路一致，计算实际真空灭弧室中不同触头间隙距离下的工频击穿场强，需要计算不同触头间隙距离下的最大宏观场致增强系数β_gmax。计算该系数首先要进行不同触头间隙距离下的电场分布仿真计算。图2-7给出了触头间隙在6mm和60mm两种极端情况下的仿真计算电场分布图。可以看出，在6mm触头间隙距离下，触头间隙的电场为均匀场，且强电场区域位于触头间隙，屏蔽筒对触头间隙的电场分布几乎没有影响。但是随着触头间隙距离的增加，强电场区域逐渐向触头侧面转移，主屏蔽筒对触头间隙电场分布影响越来越明显。在60mm触头间隙距离下，触头和屏蔽筒间隙的电场强度几乎与触头间隙的电场强度相等。

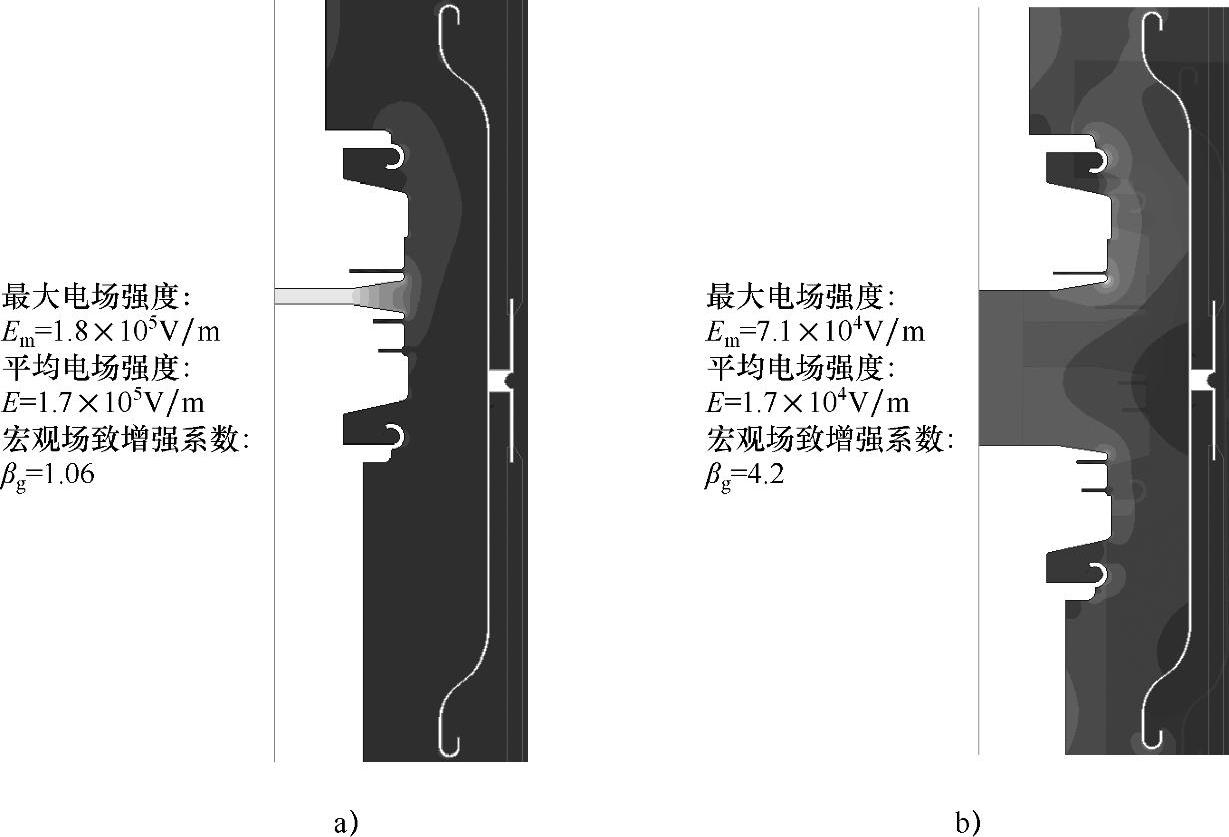
图2-7 模型真空灭弧室触头间隙电场分布图

a）开距6mm b）开距60mm

在得到模型真空灭弧室在不同触头间距下的电场分布后，根据阴极表面上的场强分布，计算出模型真空灭弧室在不同触头间隙距离下宏观场致增强系数β_g沿触头表面的分布图，如图2-8所示。然后根据得到的不同触头间隙距离下宏观场致增强系数β_g，计算出该触头间隙距离下的最大宏观场致增强系数β_gmax。最后得到最大宏观场致增强系数β_gmax与触头间隙距离的关系，如图2-8所示。从图中可以看到，最大宏观场致增强系数随触头间隙距离的增大而明显增大。

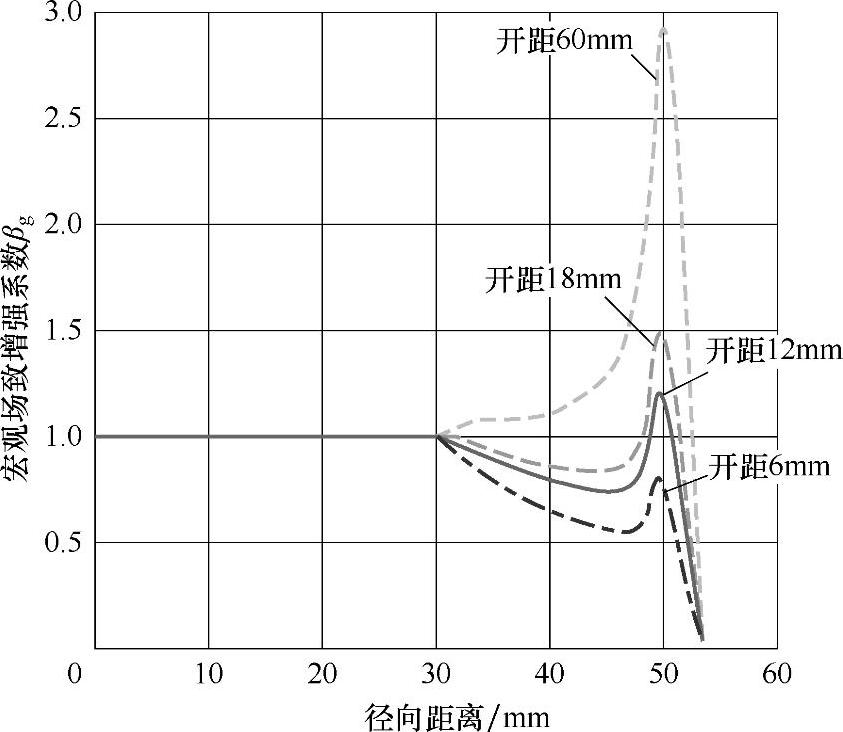
图2-8 模型真空灭弧室宏观场致增强系数β_g沿触头表面的分布

3.计算值与实验值的比较

图2-9是模型真空灭弧室不同触头间隙距离下工频击穿场强的实验值和工频击穿场强计算值的对比。从图中可以看出，工频击穿电场强度的实验结果与计算结果基本一致。

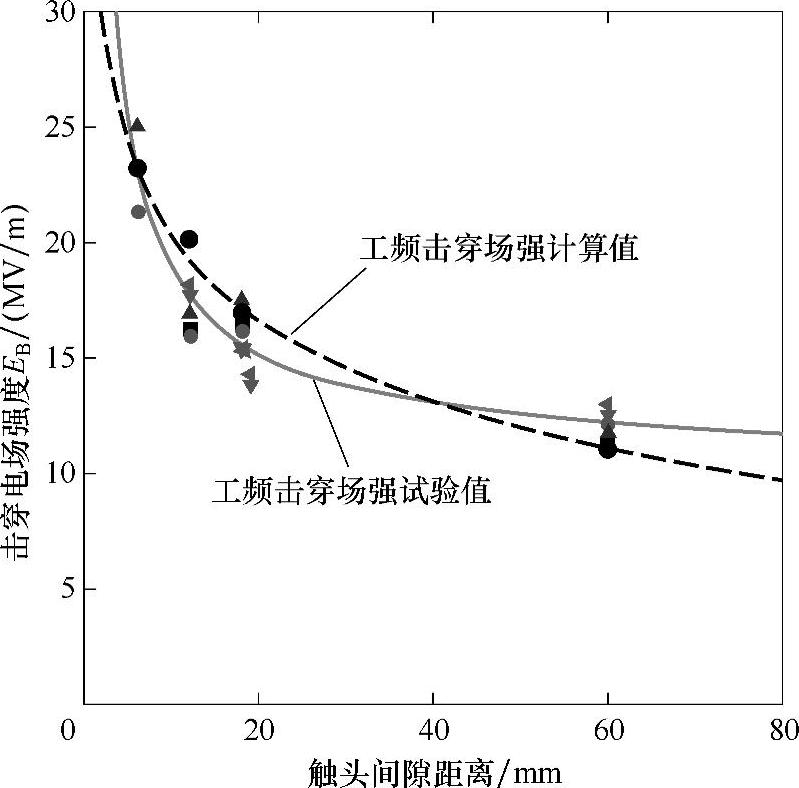
图2-9 模型真空灭弧室工频击穿场强计算值与实验值的对比