【摘要】：，xn}，求出适当的参数，使联合概率密度函数式（4-1）取得最大值。遗憾的是，最大似然估计法在大多数情况下不能用解析法求解，因而需要迭代的方法寻找优解。期望最大算法就是其中最常用的一种方法。用EM处理“不完整”的样本，即把样本点xj分为两部分，xj={xjg，xjm}。xjg表示样本，xjm=（xjm1，…，xjmK）表示丢失的数据。xjmi是1还是0，是根据xj是否属于类i有关[27]。
假设样本属于聚类簇Cj（j=1，2，…，m）的概率为P（Cj），对应各个簇的条件概率密度函数为p（x|Cj，θj），其中θj为未知参数向量。这样由m类样本组成的混合密度函数可定义为
式中：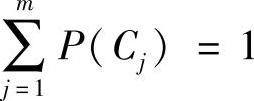
；混合概率密度的参数θ=（θ1，θ2，…，θm）。
最大似然概率（ML，Maximum Likelihood）[26]是参数估计的一种重要的方法，即对n个样本X={x1，x2，…，xn}，求出适当的参数，使联合概率密度函数式（4-1）取得最大值。
其对数的形式为
通过（∂l（θ））/（∂θi）=0求得参数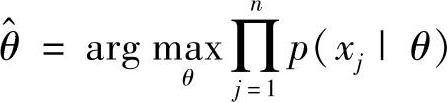
。(www.xing528.com)
遗憾的是，最大似然估计法在大多数情况下不能用解析法求解，因而需要迭代的方法寻找优解。期望最大算法就是其中最常用的一种方法。
用EM处理“不完整”的样本，即把样本点xj分为两部分，xj={xjg，xjm}。xjg表示样本，xjm=（xjm1，…，xjmK）表示丢失的数据。xjmi是1还是0，是根据xj是否属于类i有关[27]。完整数据概率对数形式为
用EM估计混合概率密度的参数时，需要首先给出参数的初始解θ（0）；再从初始解θ（0）开始，迭代地得到解θ（1），…，θ（t）。在每步迭代中，似然函数单调增加。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
