VIC模型结构及蒸发与汇流计算方法

根据VIC模型结构,模型计算主要包括以下4个方面。

1.蒸散发计算

VIC模型一般将土壤分为3层,计算过程中有时会把第1、第2层合在一起成为上层,第3层为下层。每个计算网格内陆地表面有N+1种类型,第1到第N种为植被覆盖,第N+1种代表裸土。网格内的土层间的水分交换、蒸散发及产流,是依据不同的植被类型分别计算的。网格内总的蒸散发和产流是各种地表类型上的面积加权平均值。

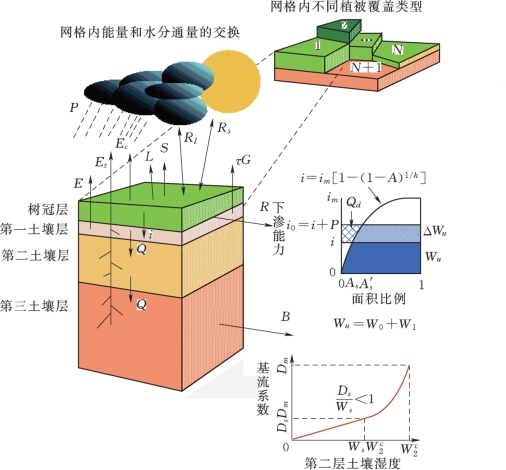
图3.1　VIC模型结构图

模型中考虑了植被冠层截留蒸发、植被蒸腾和裸地蒸发三种蒸发形式。当植被截留量不能满足大气蒸发(蒸发能力,利用Penman-Monteith公式进行计算)时,就考虑植被蒸腾；假设裸地蒸发只发生在上层,下层蒸发为零；上层土壤饱和时,蒸发等于蒸发能力；如果上层土壤不饱和,则进行相应折减,而使用的折减系数则考虑了土壤的实际含水量和最大含水量的空间不均匀分布；如果有很小的降水,蒸发则先发生在表层土壤。

计算蒸发能力的Penman-Monteith公式所需的净辐射和水汽压差不是直接给出的,而是作为日最高、最低气温的函数计算得出。大气顶层的潜辐射由纬度和儒略日(Julian day)的函数求得。可能辐射随大气透射度递减,透射度为气温变化的函数,日气温变化越大透射性越好。在海平面上最大净空气投射量为0.06。在其他应用情况下,这些参数可以按季节进行率定。

在没有大气湿度资料的情况下,把日最小温度大致作为露点温度,则水汽压差为日平均气温处的饱和水汽压与日最低气温处的饱和水汽压之差。这种近似在湿润地区具有一定的精度,但在比较干旱的气候区误差就相对较大,主要是因为干旱地区的夜最低气温常高于露点温度。因此,对于干旱和半干旱地区,需要对日最低气温处的饱和水汽压加以修正。修正方法是采用一个干旱指数,即年潜蒸发(只取决于净辐射)与年降水量的比值。当指数小于2.25时,不用进行修正,在其他情况下,以日可能蒸发与日平均降水量的比值及空气温度为基础对日最低气温处的饱和水汽压进行修正。净长波辐射则是假设日平均气温为表面温度,并把前面计算的大气透射度作为云层参数来计算。

2.融雪计算

模型融雪计算使用能量平衡的方法来表示地表的积雪和融化。假定低矮的植被完全被积雪覆盖,因此不影响地表积雪场的能量平衡。模型考虑因为升华、滴落和释放而引起的地表雪截留。此外,每个网格被细分成由使用者指定降水因子的高程带。积雪高程带代表子网格地形控制降水和气温而对积雪和融雪产生的影响。在积雪表面,使用一个两层能量平衡模型来计算地表积雪和融化。

将积雪场分为两层,考虑所有重要的热能通量(如长波、短波辐射,感热量、潜热量,对流能量)和积雪场内部的能量,而忽略地表热通量。由于积雪增加了地面反照率,减少了地表粗糙率,因此,在每一个时间步长,模型将首先计算积雪场的雨雪比例,然后计算所有的能量通量。

植被对降雪的截留量大小依据叶面面积指数(LAI)来计算,同时,最大存储量还考虑温度和风速的影响。冠层的融雪采用简化的积雪场能量平衡模型进行计算。融雪模型中有3个主要的参数需要设定:降雪发生的最高温度、降雨发生的最低温度和雪盖表面粗糙高度。通常前两个参数分别设为1.5℃和-0.5℃,表面粗糙高度的范围为0.001～0.03m。

3.产流计算

VIC模型在计算产流的同时将水源分开,上层土壤产生直接径流,下层土壤产生基流。计算的直接径流与基流之和即为网格的河网总入流。上层土壤产生直接径流及下渗到下层土壤的渗漏,下渗部分是土壤含水量和饱和水力传导度的函数,VIC模型引进新安江模型的蓄水容量曲线的概念,考虑土壤含水量分布的不均匀性对直接径流的影响。直接径流的计算公式为

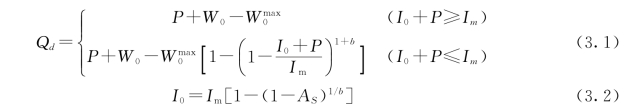
式中:P为降水量；W 0为初始土壤含水量；W max0为上层最大土壤含水量；b为形状参数；I 0为初始下渗率；I m为最大下渗容量；A S为网格内土壤达到饱和的百分数。

VIC模型下层土壤产生基流,采用Arno模型计算基流,即当土壤含水量在某一阈值以下时,基流是线性消退的,而高于此阈值时,基流过程是非线性的。基流的计算表达式为

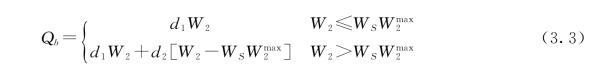
式中:d 1为下土层含水量的线性出流系数；d 2为基流非线性消退系数；W S为基流非线性消退时最大土壤含水量所占的百分比系数；W 2为下土层土壤含水量；W max2　为下土层最大含水量。

4.汇流计算

VIC模型汇流计算方案见图3.2,模型假设水流总是通过其相邻8个网格方向的1个网格流出,将各网格产生的河网总入流先汇流至网格出口,再进入河流系统,最后到达流域出口。网格内的汇流采用单位线的方法,河道汇流采用线性圣维南方程(Saint-Venant Equation)计算。

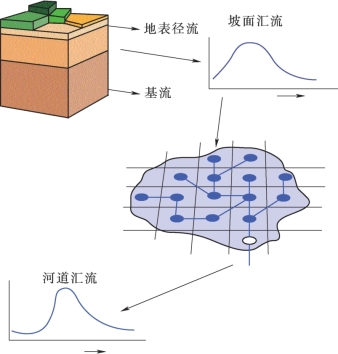
图3.2　VIC模型汇流方案图(www.xing528.com)

降雨形成的不同的径流成分的汇流历时有所不同,因此需要把流量分成快速流和慢速流两部分,公式如下:

式中:QS(t)为慢速流；QF(t)为快速流。

总流量:

假定每一个计算时段上参数k和b是常数,快速流和慢速流大致对应于产流模型的直接表面径流和基流过程,快速流和慢速流的解析关系式为

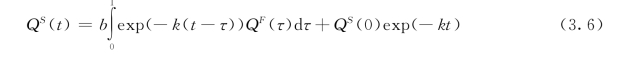
初始的QS(0)随着exp(-kΔt)项而衰减,其中,1/k是慢速流的平均驻留时间。对于离散性数据,QS(t)可由式(3.7)求解,即

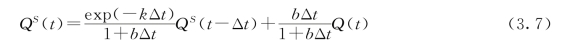
假设流量与净雨Pef f(有效降雨)具有线性关系,又因为快速流和慢速流具有式(3.6)的关系,所以可以找到一个把快速流QF和P eff联系起来的脉冲响应函数。脉冲响应函数和P eff可通过以下方程迭代求得

式中:UH F(τ)为传输过程中快速流的脉冲相应函数(瞬时单位线)；t max为快速流完全衰退的时间。

在离散情况下,式(3.8)可写成式(3.9)和式(3.10),其中,Δt为数据的时段长度,t max=(m-1)Δt。将净雨量作为起始条件代入式(3.9),并对两式迭代求解。

每一次迭代过程中对任意i,≥0须满足以下条件:

然后把UH F代入式(3.9),可求得Peff。

同理,迭代过程满足0≤≤Pi,i为任意值。然后把式(3.11)中的Peff代入式(3.9),反复计算直到收敛。

河道汇流可用线性圣维南方程表示,即

式中:C为波速；D为扩散系数,需要根据实际河道的特性来估计。

回水的影响在大尺度水文模型中很小,所以忽略不计。式(3.12)可采用脉冲响应函数(或格林函数)的卷积公式来求解。