功率谱分析可以将时间序列的能量分解到不同频率上,根据不同频率分量的方差贡献可识别出原序列的周期成分。设序列为x 1,x 2,…,x n,功率谱分析步骤如下:
步骤一:计算样本滞时j的自相关系数r(j)(j=1,2,…,m),m为最大滞时。m较大时,谱的峰值较多,但所有峰值并不表现为周期,有可能是估计偏差造成的虚假现象。m较小时,谱估计过于光滑,不容易出现峰值,难以确定出主要周期。因此,m选取十分重要,一般取m=n/3～n/10,n不大时,可取m=n/2。
步骤二:计算不同波数k下的粗功率谱,即
在实际计算中考虑端点特性,常采用下列形式:
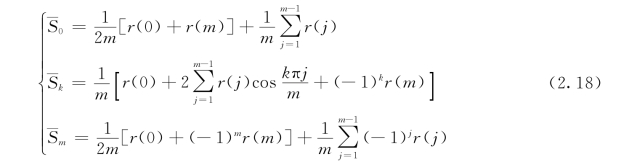
步骤三:粗功率谱与真实谱Sk有一定误差,需要平滑处理。当采用Hanning窗时,平滑公式为
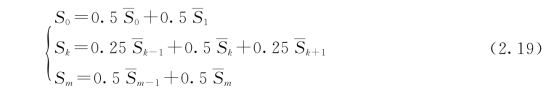
步骤四:以k为横轴,Sk为纵轴绘制功率谱图。峰值对应的波数k相应的T有可能为周期,T=2m/k。
步骤五:周期T是否显著,必须进行检验。首先判断样本序列总体谱类型。当r(1)＞ρcα时,序列可能来自红噪声,则总体谱取红噪声谱；反之,取白噪声谱。
对于红噪声,其标准谱为
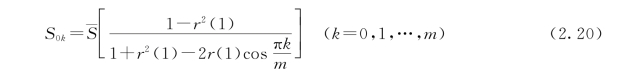
其中
对于白噪声,其标准谱为
式中: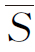
同前。
构造统计量:(www.xing528.com)
式中:α为给定的显著性水平；χ2(α)为遵从自由度为υ的χ2分布,其中υ=(2n-0.5m)/m。当Sk＞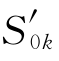
时,表明k对应的周期是显著的；反之,周期不显著。
ρcα计算如下:
式中:tα为显著性水平α的自由度为n-2的t分布临界值。
2.小波分析法
小波分析是一种可调时频窗的分析方法,能对时间序列进行多时间尺度分析。通过对年径流序列小波分析,可以得到一些主要尺度的变化过程,进而分析序列周期特性。小波分析的关键是小波变换。对于时间序列,小波变换为
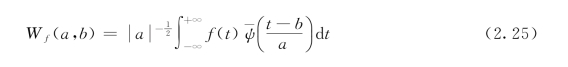
式中:a为尺度因子,1/a在一定意义上对应于频率ω,反映小波的周期长度；b为时间因子,反映时间上的平移；ψ(t)为母小波；W f(a,b)为小波变换系数。
实际上时间序列常是离散的,其离散形式可表示为
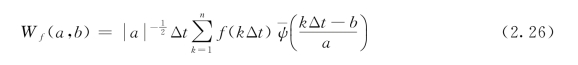
式中:k=1,2,…,n；Δt为取样时间间隔。W f(a,b)能同时反映时域参数b和频域参数a的特征,它是时间序列f(t)或f(kΔt)通过单位脉冲相应的滤波器的输出。当a较小时,对频率的分辨率低,对时域的分辨率高；当a增大时,对频率的分辨率高,对时域的分辨率低。
W f(a,b)随参数a和b变化而变化,可作出以b为横坐标,a为纵坐标的关于W f(a,b)的二维等值线图,称为小波变换系数图。通过小波变换系数图可得到关于时间序列变化的小波变化特征。在尺度a相同情况下,小波变换系数随时间的变化过程反映了系统在该尺度下的变化特征:正的小波变换系数对应于偏多期,负的小波变换系数对应于偏少期,小波变换系数为零对应突变点；小波变换系数绝对值越大,表明该时间尺度变化越显著。
母小波函数采用Morlet复小波,表示为ψ(t)=e ict e-t2/2。运用小波方法对序列进行多尺度分析,进而了解序列在不同时间尺度上的变化。为方便计算,将序列距平化处理,计算小波变换系数。
将时间域上关于尺度a的所有小波变换系数的平方进行积分,即小波方差为
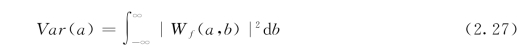
在一定尺度下,Var(a)表示序列中该尺度周期波动的强弱(能量大小)。小波方差随尺度变化的过程,称为小波方差变化图。通过此图可确定一个时间序列存在的主要时间尺度,即主周期。
Morlet小波的时间尺度a与周期T有如下关系:
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
