逻辑函数及其常见表示方法

所谓逻辑关系,是指条件和结果之间的关系。用于反映和处理这种逻辑关系的数学工具就是逻辑代数。逻辑代数又称布尔代数,有输入变量(自变量)和输出变量(因变量),并用英文字母A,B,C,…表示。但在逻辑代数中,变量的取值只有0和1,并且0和1不再表示变量具体的数量大小,而是表示事物两种相反的状态。若定义电位的高(高电平)为1,电位的低(低电平)为0,则称为正逻辑;电位的高为0,电位的低为1,则称为负逻辑。本书在讨论中采用正逻辑。

逻辑函数及其表示方法如下:

(1)常用的逻辑运算

在逻辑代数中,基本的逻辑运算有与、或、非3种。

1)与运算

“决定事件发生的几个条件全部具备时,事件才会发生”。这种因果关系称为与逻辑关系。用以实现与逻辑关系的电路,称为与门。与门逻辑符号如图10.1.4(b)所示。

如图10.1.4(a)所示的串联开关电路,若以开关的闭合为条件具备,灯亮为事件发生,则只有A、B开关都闭合时,灯Y才会亮,有一个开关断开,灯都不会亮。这里开关A、B的闭合与灯亮的关系为与逻辑关系,对应的运算为与运算。与运算可表示为

式中,符号“·”表示逻辑乘,读作“与”。为了书写方便,常将“·”省略,写为Y=AB。

图10.1.4　与逻辑

表10.1.3　与逻辑真值表

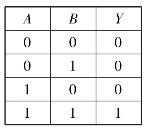
如果设开关闭合为1,断开为0,灯亮为1,灯灭为0,则A、B的全部状态组合与Y之间的对应关系见表10.1.3,该表为与逻辑真值表。由与逻辑真值表可将与逻辑关系概括为:有0出0,全1出1。

2)或运算

“决定事件发生的几个条件中只要有一个条件具备,事件便会发生”。这种逻辑关系称为或逻辑关系。实现或逻辑关系的电路,称为或门。或门逻辑符号如图10.1.5(b)所示。

如图10.1.5(a)所示的并联开关电路,只要有一个开关闭合,灯就亮。当两个开关全部断开时,灯才会灭。这里开关的闭合与灯亮的关系为或逻辑关系,对应的运算为或运算。或运算可表示为

式中,符号“+”表示逻辑加,读作“或”。或逻辑真值表见表10.1.4。或逻辑关系可概括为:有1出1,全0出0。

图10.1.5　或逻辑

表10.1.4　或逻辑真值表

3)非运算

决定事件发生的条件只有一个,当条件具备时事件不发生,条件不具备时事件反而发生。这种逻辑关系,称为非逻辑关系。实现非逻辑关系的电路,称为非门。其逻辑符号如图10.1.6(b)所示。

如图10.1.6(a)所示的电路,当开关闭合时灯灭,而当开关断开时灯反而亮。这里开关闭合与灯亮是非逻辑关系。对应的运算为非运算。非运算可表示为

式中,字母上面的符号“—”读作“非”或“反”。非逻辑真值表见表10.1.5。

图10.1.6　非逻辑

表10.1.5　非逻辑真值表

实际的逻辑运算往往较复杂,但可用基本逻辑运算组合而成,称为复合逻辑运算。复合逻辑运算顺序与普通代数一样,首先算括号里的内容,然后再算与,最后才能算或。先或后与的运算式,或运算要加括号。例如,(A+B)·(C+D)不能写成A+B·C+D。

4)与非运算

先与运算后非运算组合成与非运算。与非运算表示为

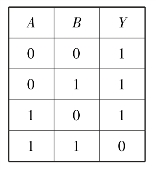
与非逻辑真值表见表10.1.6。与非逻辑关系可概括为:有0出1,全1出0。

与非门逻辑符号如图10.1.7所示。

表10.1.6　与非逻辑真值表

图10.1.7　与非门逻辑符号

5)或非运算

先或后非运算组成或非运算。或非运算表示为

或非逻辑真值表见表10.1.7。或非逻辑关系可概括为:有1出0,全0出1。或非门逻辑符号如图10.1.8所示。

6)与或非运算

按照与或非顺序,将与运算、或运算、非运算组合组合起来,就能实现与或非逻辑运算。与或非运算表示为

与或非门逻辑符号如图10.1.9所示。

表10.1.7　或非逻辑真值表

(www.xing528.com)

图10.1.8　或非门逻辑符号

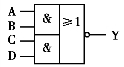
图10.1.9　与或非门逻辑符号

7)异或运算

“决定事件的发生有两个条件,两个条件相异时,事件就会发生;两个条件相同时,事件不会发生”。这种因果关系称为异或逻辑关系。异或运算表示为

通常写作Y=A⊕B,符号“⊕”表示异或逻辑运算。异或逻辑真值表见表10.1.8。异或逻辑关系可概括为:相异出1,相同出0。异或门逻辑符号如图10.1.10所示。

表10.1.8　异或逻辑真值表

图10.1.10　异或门逻辑符号

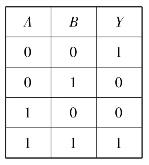
8)同或运算

“决定事件的发生有两个条件,两个条件相同时,事件就会发生;两个条件不同时,事件不会发生”。这种因果关系称为同或逻辑关系。同或运算表示为

通常记为Y=A☉B。符号“☉”表示“同或”逻辑运算。逻辑真值表见表10.1.9。同或逻辑关系可概括为:相同出1,相异出0。同或门逻辑符号如图10.1.11所示。

表10.1.9　同或逻辑真值表

图10.1.11　同或门逻辑符号

比较表10.1.8和表10.1.9还可知,异或运算和同或运算是互为相反的运算,即

也可记为

(2)逻辑函数的表示方法

数字电路讨论的各种逻辑关系可描述为

式中,A、B、C为输入变量,Y为输出变量。输入变量与输出变量之间的关系是一种函数关系,这种函数关系称为逻辑函数。逻辑函数有多种表示方法。常用的有逻辑函数式、真值表、逻辑图、波形图等。下面举例说明。

例如,如图10.1.12所示的电路,若以开关闭合为条件具备,灯亮为事件发生,试用逻辑函数式、真值表、逻辑图、波形图表示该电路的逻辑关系。

1)逻辑函数式

用常用的逻辑运算来表示输入变量与输出变量之间的因果关系式,称为逻辑函数式。如图10.1.12所示电路灯亮的逻辑函数式为

一个逻辑函数的表达式可以有多种形式。最常用的是与或式。例如,Y=AB+C就是与或式。

2)逻辑状态表

将输入变量的全部取值组合与对应的函数值排列成表格,即为真值表。若输入变量为n个,每个输入变量有0、1两个取值,则输入变量共用2n个取值组合。如图10.1.12所示的电路有A、B、C 3个开关,即3个输入变量。因此,输入变量共有23=8种取值组合。设开关闭合为1,断开为0,灯亮为1,灯灭为0,则将输入变量的8种取值组合及对应的函数值列成的真值表见表10.1.10。

表10.1.10　如图10.1.12所示电路的真值表

真值表表示了逻辑函数值与逻辑输入变量各种取值之间的对应关系。由真值表写出的逻辑函数式,称为标准与或式。逻辑函数的标准与或式是唯一的。书写标准与或式的步骤如下:

a.找出真值表中逻辑函数值为1的输入变量的组合。

b.每一组输入变量组合对应一个与组合,组合中取值为1的用原变量表示,取值为0的用反变量表示(变量上面有非号的变量,称为反变量;无非号的变量,称为原变量)。

c.将这些与组合进行或运算,就得到逻辑函数式。

由表10.1.10写出的标准与或式为

3)逻辑图

用常用门电路的逻辑符号将对应逻辑关系表示出来就是逻辑图。如图10.1.12所示电路的逻辑图如图10.1.13所示。

图10.1.13　如图10.1.12所示电路的逻辑图

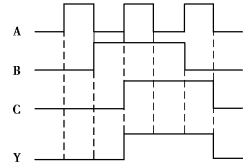
图10.1.14　如图10.1.12所示电路的波形图

4)波形图

输入变量组合与对应的函数值随时间变化的图形为逻辑函数的波形图,波形图又称时序图。如图10.1.12所示的电路,依据输入变量A、B、C的波形画出的输出端Y的波形如图10.1.14所示。波形图能直观表达输入变量和函数值之间随时间变化的规律。因此,在数字电路的分析、设计中应用较多。