正弦交流电路功率计算

(1)瞬时功率

在如图3.7.1所示的无源线性二端网络中,设端口电压和电流为,则瞬时功率为

整理上式,可得

式(3.7.1)表明,瞬时功率由两部分组成:一部分为与时间无关的常量,通常被认为是耗能元件上的瞬时功率;另一部分为正弦量,其频率2倍于电压或电流的频率,通常被认为是储能元件上的瞬时功率。在每一瞬间,电源提供的功率一部分被耗能元件消耗,一部分与储能元件进行能量交换。根据式(3.7.1)可画出电压u、电流i及瞬时功率p的波形图,如图3.7.2(a)所示。

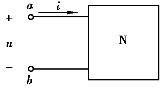
图3.7.1　无源线性二端网络

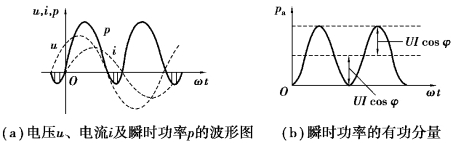
图3.7.2　无源二端网络的瞬时功率和平均功率

(2)有功功率和功率因数

在一个周期内,对瞬时功率求平均值便可得到网络的有功功率(平均功率)为

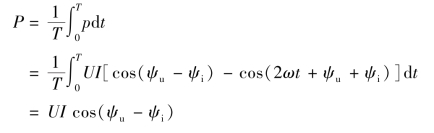
上式可写为

式中,cosφ称为功率因数,通常用λ表示,即λ=cosφ。当功率因数cosφ=1时,φ=0°,电路为纯电阻电路,网络的有功功率;当功率因数cosφ=0时,电路为纯电抗电路,网络的有功功率P=0。(www.xing528.com)

(3)无功功率

如前所述,单一参数的正弦交流电路中,QL=UL I,QC=UC I。对于RLC串联的正弦交流电路而言,无功功率Q应等于电路所有电感和电容无功功率之和。由于相位相反,QL和QC的作用也是相反的。若取QL为正值,则QC为负值,即

在如图3.4.2所示的电压三角形中,UX=U sinφ,则

需要说明的是,“无功”的意义是“交换”而不是“消耗”,“无功”不等于“无用”。很多应用电磁感应原理工作的设备就是依靠与外电路之间进行能量交换来工作的。

(4)视在功率

视在功率通常是指电源的容量。在电工技术中,将电源电压与电流的有效值乘积,称为视在功率,用符号S表示,即

视在功率的单位为伏安(V·A),反映了电源设备可能提供的最大功率。

将前面介绍的电压三角形各边对应的电压的有效值都乘以电流的有效值,也可得到有功功率P、无功功率Q和视在功率S,即

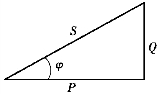
图3.7.3　功率三角形

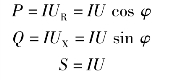
P、Q、S构成一个新的直角三角形,与电压三角形相似,称为功率三角形,如图3.7.3所示。由功率三角形可得