电路谐振及选择性与通频带

在含有电抗的正弦交流电路中,端口电压与电流同相位的现象,称为谐振。谐振电路会产生过电压或过电流。在实际应用中,为了既能利用电路的谐振又能避免它所产生的危害,有必要充分认识谐振现象,并研究谐振条件、谐振频率和谐振电路的特征。谐振可分为串联谐振和并联谐振。这里以串联谐振电路为例介绍谐振电路的分析方法。

(1)谐振的条件

由前面的讨论可知,对R、L、C串联交流电路,其阻抗为

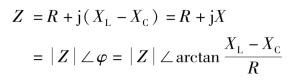
当满足XL=XC的条件时,电路呈电阻性,其端口电压与电流同相,即

式中,ω0称为谐振角频率。由于ω=2πf,则

式中,f0称为谐振频率,反映了串联电路的一种固有性质,故称固有频率,对每一个RLC串联电路,总有一个对应的谐振频率f0。

当电路参数L和C一定时,可改变电源的频率使电路谐振;当电源的频率f0一定时,可改变电容C或电感L,使电路谐振。在实际中,通常通过调节电容C使电路谐振。

(2)谐振电路的特征

串联谐振电路的基本特征如下:

①电路的阻抗|Z|最小,则

阻抗|Z|随频率变化的曲线如图3.6.1(a)所示。

一般将串联电路谐振时的感抗或容抗,称为特性阻抗,用ρ来表示,即

②在电源电压值不变的情况下,电路中的电流在谐振时达到最大值,即

阻抗模电流I随频率变化的曲线如图3.6.1所示。

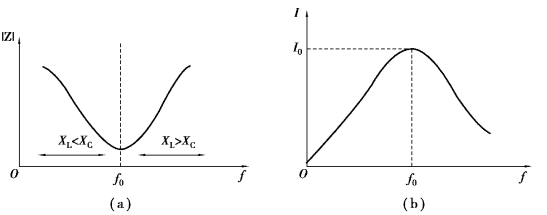
图3.6.1　阻抗模Z 、电流I随频率变化的曲线

③谐振时,电感和电容上的电压大小相等,相位相反,相互抵消。电源电压相量图如图3.6.2所示。

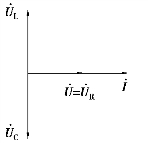
图3.6.2　串联谐振时的相量图

谐振时,UL或UC与电源电压U之间的比值,称为品质因数,用Q表示,即

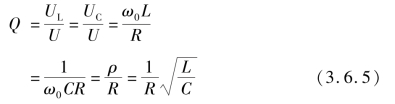
串联谐振电路中,XL=XC并远大于R,电感和电容上的电压值相等,为端口电压的Q倍,故串联谐振又称电压谐振。电路的Q值一般为50～200。因此,即使端口电压不高,谐振时电感和电容上的电压仍有可能很高。对于电力系统来说,由于端口电压本身较高,如果电路在接近于谐振的情况下工作,在电感和电容两端将出现过电压,从而击穿电气设备的绝缘层。因此,在电力系统中应避免谐振的发生。在电子电路中,可利用谐振获得较高的电压,达到选出所需信号的目的。

(3)谐振电路的选择性与通频带

当含有多种频率成分的信号电流通过谐振电路时,可从多种频率信号中选择出谐振频率的信号,这种能力称为选择性。(www.xing528.com)

品质因数Q值的大小可反映电路选择性的好坏。Q与谐振曲线的关系如图3.6.3所示。可知,曲线越尖锐,说明电路的选择性越好。

图3.6.3　不同Q值的谐振曲线的关系

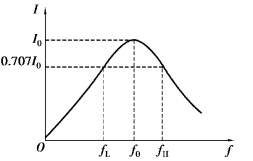
图3.6.4　通频带宽度

工程上规定:对应于0.707I0的两个频率之间的宽度,称为通频带,如图3.6.4所示。通频带规定了谐振电路允许通过信号的频率范围。依据通频带宽度,也可说明电路选择性的好坏。通频带越窄,曲线越尖锐,电路的选择性则越好。

通常通频带宽度可用公式求得,即

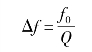
下限频率和上限频率为

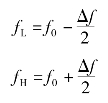
应当说明的是,品质因数Q越高,电路的择性越好,但通频带越窄。因此,工程中对品质因数Q和通频带Δf要综合考虑。

【例3.6.1】　某收音机的输入回路(调谐回路)可简化为一个由R、L、C组成的串联电路。已知电感L=250μH,R=20Ω,今欲收到频率范围为525～1 610 kHz的中波段信号,试求电容C的变化范围。

解　由式(3.6.1)可知当f=525 kHz时,电路谐振,则

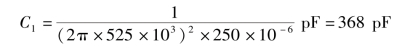
当f=1 610 kHz时,电路谐振,则

因此,电容C的变化范围为39.1～368 pF。

【例3.6.2】　一个C=300 pF的电容和一个线圈组成串联谐振电路,线圈的电感L=0.3 mH,电阻R=10Ω。若电路输入端的信号电压U=1mV,求谐振频率f0、谐振电流I0、品质因数Q及电容电压UC。

解　谐振频率为

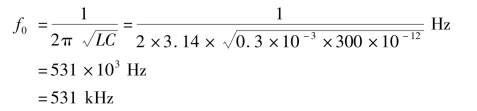
谐振电流为

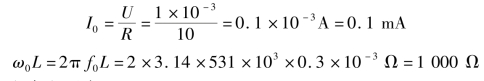
品质因数和电容电压为

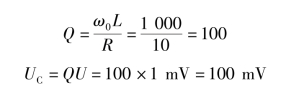
在工程中,也常用到电感线圈(R、L的串联)与电容组成的并联电路。并联谐振时,电路阻抗模最大,总电流最小,电感和电容上会产生大电流,为总电流的几十倍至几百倍,故并联谐振又称电流谐振。当电源为某一频率时,电路的阻抗模最大,电流通过时在电路两端产生的电压也最大。当电源为其他频率时,电路不发生谐振,阻抗模较小,电路两端的电压也较小,这样就起到了选频的作用。

【思考与练习】

3.6.1　为什么将串联谐振又称电压谐振?

3.6.2　RLC串联电路中,若R=10 kΩ,L=0.1 mH,C=0.4 pF,US=0.1 V,则此电路的特性阻抗ρ及品质因数Q分别为多少?谐振时UC为多少?