复数的基本形式及运算法则

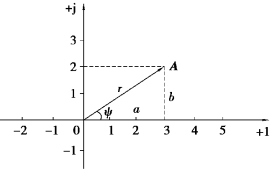
图3.2.1　复数

(1)复数的基本形式

在直角坐标系中,以横轴为实数轴,纵轴为虚数轴,构成的平面称为复平面。复平面内任意一个矢量(有向线段)都可用复数来表示。

复数有多种表达形式。常见的有4种表示式。如图3.2.1所示的矢量A,它的4种复数表示式如下:

1)代数式

式中,a称为实部,b称为虚部,j为虚数单位。定义虚数单位为

即j2=-1。某量乘以j意味着其沿逆时针方向旋转90°,值不变;某量乘以-j意味着其沿顺时针方向旋转90°,值不变。故虚数单位j又称90°旋转因子。

2)极坐标式

在图3.2.1中,复数A与实轴正方向的夹角为ψ,则其极坐标式为

式中,r称为模,称为辐角复数A的实部a、虚部b与模r构成一个直角三角形。

3)三角函数式

三角函数式为

(www.xing528.com)

4)指数式

将欧拉公式ejψ=cosψ+j sinψ代入式(3.2.4)中,可将三角函数式转换为指数式,即

以上4种表示式可相互转换。用复数进行运算时,代数式常用于复数的加减法运算,极坐标式常用于复数的乘除法运算。

(2)复数的运算法则

设两个复数:A1=a1+j b2=r1∠ψ1,A2=a2+j b2=r2∠ψ2,则运算法则如下:

①加减法运算:A1±A2=(a1±a2)+j(b1±b2)。

②乘法运算:A1×A2=r1×r2∠(ψ1+ψ2)。

③除法运算

【例3.2.1】　已知A1=8-j6,A2=3+j4。试求:

(1)A1+A2;

(2)A1×A2。

解　(1)A1+A2=(8-j6)+(3+j4)=11-j2

乘法运算时,首先应将直角坐标式转换为极坐标式,然后再进行运算,即

(2)A1×A2=(10∠-36.9°)×(5∠53.1°)=50∠16.2°