正弦量的初始值简介

式(3.1.1)中的(ωt+ψ),称为正弦量的相位角,简称相位,单位为弧度(rad)。它反映了正弦量变化的进程。t=0的瞬间,称为正弦量的计时起点(坐标原点);t=0时的相位角,称为正弦量的初相位,简称初相,记为ψ。其定义域为-π～π。t=0时,正弦量的瞬时值称为正弦量初始值。不同初相正弦电压的波形图如图3.1.2所示。

图3.1.2　不同初相正弦电压的波形图

可知,选择的计时起点不同,正弦量的初相不同,初始值也不同。由波形图确定初相的方法如下:

(1)初相大小的确定

计时起点与距计时起点最近的正半周起点(正弦量由负值变化到正值经过的零值点)之间的角度(或电角度)为初相。

(2)初相正负的确定

初始值为正,初相为正;初始值为负,初相为负。

【例3.1.1】　已知某工频正弦电压如图3.1.3所示。试写出该电压的瞬时值解析式。

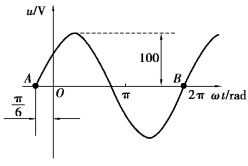
图3.1.3　例3.1.1波形图

解　由已知得

则

(www.xing528.com)

由波形图可知,A、B两点均为正半周起点,但A点是距计时起点最近的正半周起点,因此,初相的大小为由初始值为正,可确定初相为正值。因此

另外,由波形图可知电压的最大值为

电压的瞬时值解析式为

两个正弦量相位的差值称为相位差,用符号φ表示,其定义域为-π～π。相位差φ用来比较两个同频率正弦量的变化步调(到达最大值或零值的先后)。假设有两个正弦量,其瞬时值解析式分别为u=Um sin(ωt+ψu),i=Im sin(ωt+ψi),则相位差为

可知,同频率正弦量相位差等于它们的初相之差。若φ=|ψu-ψi|>π,则可应用三角函数知识将相位差变换到绝对值小于π的范围内。下面对相位差进行讨论:

①当ψu=ψi,即相位差φ=0,说明u和i同时到达对应的零值点(或正的最大值点)说明u与i步调一致,此时称在相位上u与i同相,如图3.1.4(a)所示。

②当ψu与ψi相差±π,即相位差φ=±π,说明u比i先半个周期到达对应的零值点(或正的最大值点),此时称在相位上u与i反相,如图3.1.4(b)所示。

③当ψu>ψi,即相位差φ>0,此时称在相位上u比i超前φ角,或者说i比u滞后φ角,如图3.1.4(c)所示。

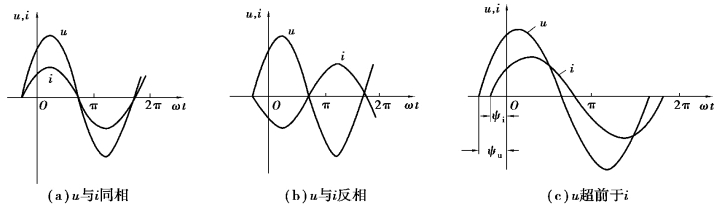
图3.1.4　正弦量的相位差