(1)换路定则
前已述及,在换路瞬间电容两端的电压和流过电感的电流是连续变化的。因此,电路在换路瞬间,电容的电压uC、电感的电流iL不能跃变,这就是换路定则。
通常将换路瞬间用t=0表示,并用t=0-表示换路前最后的一个瞬间,用t=0+表示换路后最初的一个瞬间,则换路定律也可描述为

需要说明的是,除电容的电压uC和电感的电流iL以外,电路中其他各处的电压、电流在换路前后是可能发生跃变的。
(2)初始值的确定
电路中各元件的电压和电流在换路后的最初一个瞬间(即t=0+)的值,称为暂态过程的初始值。若用f代表电流或电压,则其初始值记为f(0+)。初始值的求解步骤如下:
①画出换路前最后一瞬间(t=0-)的等效电路(电容元件视为开路,电感元件视为短路),求出uC(0-)和iL(0-)。
②依据换路定则确定uC(0+)及iL(0+)。
③画出换路后最初的一瞬间(t=0+)的等效电路(电容元件用等值电压源代替,电感元件用等值电流源代替),依据电路结构,求出其余的初始值。(https://www.xing528.com)
【例2.6.1】 如图2.6.1(a)所示的电路,在t=0时换路(开关S打开),设换路前电路已处于稳态,求初始值uC(0+)、i(0+)。
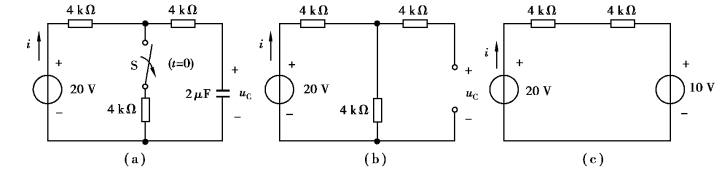
图2.6.1 例2.6.1的图
解 (1)画出电路在t=0-时刻的等效电路,如图2.6.1(b)所示,因换路之前电路已处于稳态,此时电容的电流为零,电容可视为开路。依据t=0-时刻等效电路可求得电容两端的电压uC(0-),即
![]()
(2)由换路定律得
![]()
(3)画出t=0+时的等效电路,如图2.6.1(c)所示。依据t=0+时刻的等效电路,列KVL方程,求得i(0+),即
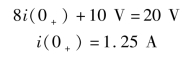
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




