【摘要】：以InAs／AlSb异质结为例，来定量描述界面处形成的三角形势阱中二维电子气的特征。由式2-1、2-3可得到：把公式2 5带入公式2-4可得：解微分方程，其解是Airy函数：界面条件为：能量Ez满足：故Ez取下值：从上式看到界面处三角形势阱中电子是量子化，三角势阱中出现一系列分立的能量值，越高能量值距离越近，直到趋于连续。图2.5InAs／AlSb界面上势能的分布
以InAs／AlSb异质结为例，来定量描述界面处形成的三角形势阱中二维电子气的特征。薛定尔方程中描述电子波函数：
近似的三角势阱中有：
此处，界面势阱电场用Fs表示。由式2-1、2-3可得到：
把公式2 5带入公式2-4可得：
解微分方程，其解是Airy函数：
界面条件为：
(www.xing528.com)
能量Ez满足：
故Ez取下值：
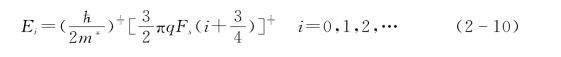
从上式看到界面处三角形势阱中电子是量子化，三角势阱中出现一系列分立的能量值，越高能量值距离越近，直到趋于连续。上面是用三角形势阱来近似定量表达了界面处2DEG 量子化，但实际势阱的形状不一定是三角形的，材料中电离杂质电荷，载流子电荷等综合决定了势阱形状。由泊松方程：
此处，电离杂质电荷分布表示为ρD（Z），电子电荷的分布由ρe（Z）表示，ρe（Z）表示为：
式中Nn 表示第n 个子带的电子数，本征值En 的波函数标记为ψn（Z），势能V（Z）表示异质结界面处的有限势垒。界面由能带不连续而形成的势垒、势阱中大量电子相互作用产生的电势以及库伦电势这三部分组成。图2.5给出了有限高势垒（N-AlGaAs／GaAs）的自恰解。
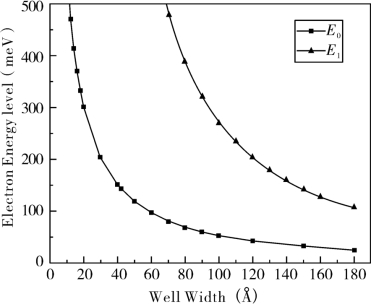
图2.5 InAs／AlSb界面上势能的分布
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
