非结构化网格的最新发展——1.8.2版本

非结构化网格节点之间的邻接是无序的、不规则的，每个网格点可以有不同的邻接网格数。非结构化网格如图1-8所示。

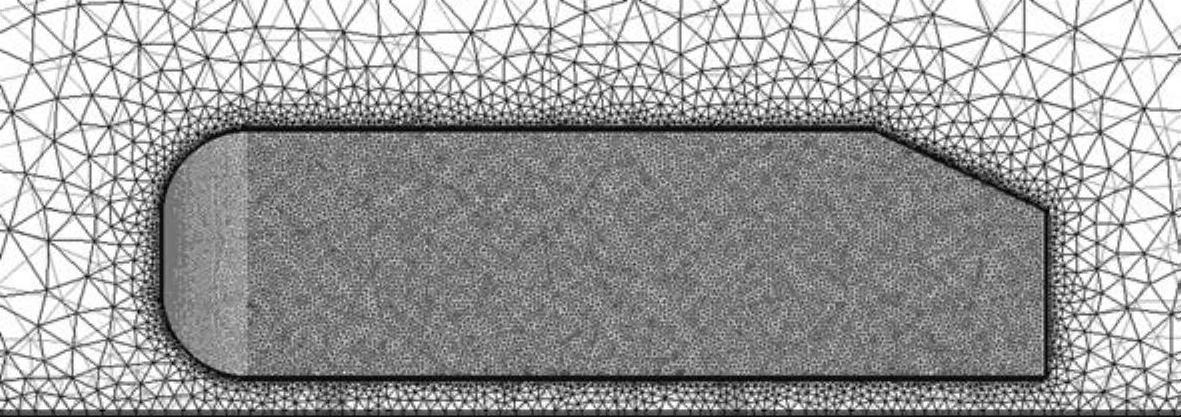
图1-8 非结构化网格

与结构化网格相比，非结构化网格有以下优点：

1）能够离散具有复杂外形的区域，因为非结构化网格单元可以在任意计算区域中完全填充到整个空间，能相当精确地表示出物体的边界，从而保证在边界处的初始准确度。

2）能够快速地在网格中增加、删除节点，处理动边界问题比较方便。

3）能够很容易地采用自适应网格方法提高解的质量。

当然，非结构化网格生成方法也存在先天的不足，那就是它需要较大的内存空间和较长的CPU时间，计算分辨率较差，且不适于黏性流场的求解。目前，非结构化网格方法已广泛应用于定常气动流场数值模拟中。(https://www.xing528.com)

非结构化网格的划分方法大体上可以分为3类：第一类是八叉树（Octree）方法，第二类是Delaunay方法，第三类是锋面推进（Advancing Front）法。

八叉树方法于20世纪80年代由Mark Shephard首创，是一种先用六面体网格剖分流场，再在六面体内部增加节点，将原有网格单元剖分为更小的单元，直到满足网格精度的方法。在二维情况下，其初始网格为四边形网格，相应的网格划分方法称为四叉树（Quadtree）方法。

Delaunay方法指的是一大类方法，这些方法的共同特点是在网格剖分的过程中满足Delaunay准则。Delaunay准则又称空心球（Empty Sphere）准则，其含义是过三角形3个顶点的圆或过四面体4个顶点的球的内部不能包含其他网格单元的节点。当然，这里的“其他网格的节点”不包括与当前网格单元共用的那些节点。Delaunay方法在具体划分网格时可以先将流场划分为粗大的网格，然后通过向初始网格内部插入新的网格节点的方式逐渐使之细化，直到网格密度满足密度函数的要求，或者网格尺度满足尺度函数的要求为止；也可以先划分边界网格，再从边界网格根据Delaunay准则向流场内部推进（类似于后面的锋面推进法）；还可以先根据Delaunay准则生成内部网格，再根据边界网格的约束条件对网格进行修正，以得到最终计算所需的网格。

锋面推进法是由美国George Mason大学的Rainald Lohner和中国香港大学的S.H.Lo发展起来的。锋面推进法在网格划分的过程中，首先要在边界上划分好三角形单元，然后再根据边界上的三角形的3个顶点计算、确定第4个顶点，最终构成新的四面体。整个网格的划分过程是从边界向流场内部推进的，推进过程中存在一个“锋面”，直到从各个边界上的锋面相遇并融合，网格划分过程才结束。在锋面推进过程中，基于原有三角形边界面得到的第4个顶点，可以是新生成的顶点，也可以是流场中原来存在的节点。究竟采用原有节点，还是需要新生成一个节点，都取决于对网格划分进行控制的尺度函数。在网格推进的过程中，除了要生成、确定第4顶点外，还要判断来自各个边界的锋面是否发生冲突和重叠，最后得到满足网格密度或尺度要求的网格。

无论何种网格划分方法，其网格密度通常都依赖于流场的结构。在流场变量变化梯度较大的地方，如边界层内部、激波附近区域或分离线附近，需要较大的网格密度，而在流场变量较平缓的区域，则可以适当减小网格密度，以节省计算机资源。

网格在根据几何方法生成后，还必须进行光顺处理，即对畸变率较大的网格进行重新划分或调整。在实际的网格生成过程中，一方面可以通过网格的长宽比确定网格的畸变率，另一方面还可以通过控制每个网格节点夹角的方式控制畸变率。

畸变率对于计算结果的影响也与畸变网格所处的位置有关。如果畸变较大的网格处于流场变量梯度较大的区域，则由畸变带来的误差就比较大，对计算结果的影响也比较严重。如果畸变较大的网格位于流场变量变化平缓的区域，则带来的误差及其影响相对而言就比较小。因此，能否正确地划分网格在很大程度上依赖于对流场流动机理的把握和对流场结构的预判。