壁面函数法：流动计算高效精确的方法

壁面函数法不对黏性影响比较明显的区域（黏性底层和过渡层）进行求解，而是用一组半经验公式（即壁面函数）将壁面上的物理量与湍流核心区内的相应物理量联系起来。采用壁面函数法的半经验公式可解决壁面对流动的影响，对受黏性力影响的区域（黏性力层及过渡层），其壁面方程的运用能够很好地修正湍流模型。对于大多数高雷诺数的流动，壁面函数法能充分节省计算资源，因为在近壁面黏性力影响区域，由于变量变化太快，不需要解决，所以这种方法经济、实用而且很精确，很受欢迎。

壁面函数法的基本思想为：对于湍流核心区的流动，采用k-ε模型求解，而不求解壁面区，换为直接采用半经验公式将壁面上的物理量与湍流核心区内的求解变量联系起来，这样不经过对壁面区内的流动进行求解，就可以直接得到与壁面相邻控制容积的节点变量值。

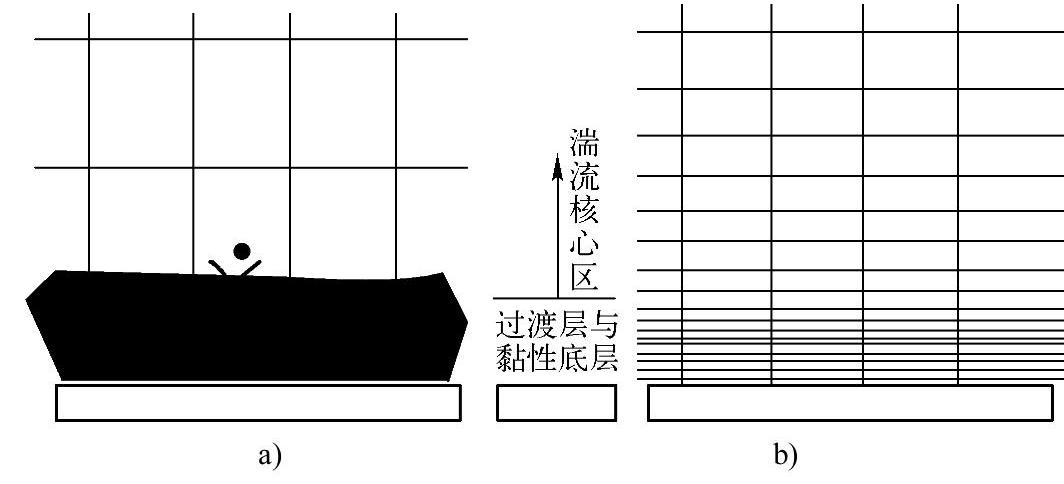
划分网格时，壁面函数法不需加密壁面区，只需将第一个内节点布置在对数律成立的区域内，即放置到湍流充分发展区域，如图1-4a所示。图中的阴影部分为壁面函数公式有效的区域，阴影以外的网格区域为采用高Re数k-ε模型进行求解的区域。壁面函数如同一架桥梁，将壁面值同相邻控制容积的节点变量值联系起来。

(www.xing528.com)

图1-4 求解壁面区流动的两种方法所对应的计算网格

a）壁面函数法对应的计算网格 b）低Re数k-ε模型对应的计算网格

通常用壁面函数来表示边界层的速度、温度和湍流能量等物理量的分布。在边界层区域，流体的湍流效应十分显著，高雷诺数模型在此区域内就不再适用了，有时为了减少在壁面附近网格的数量，又不得不采用高雷诺数k-ε模型，故采用壁面函数法来计算壁面处的湍流物理量。对于大多数高雷诺数的流动，壁面方程法能充分节省计算资源，因为在近壁面粘性力影响区域，由于变量的变化太快，不需要解决，所以这种方法经济、实用，而且很精确，很受欢迎，对于这种工业上的流动模拟，这是一个很好的方法。然而，壁面方程法运用在低雷诺数流动区域却并不理想，其所依赖的壁面方程的假设不再成立，在这种情况下，需要用“近壁面模型”来解决黏性力影响区域的流动。