近壁面处理方法：壁面函数与低Re数k-ε模型

湍流流动受壁面影响很大，很明显，平均流动区域将由于壁面不光滑而受到影响。当然，湍流还受到壁面产生的其他影响。在离壁面很近的地方，黏性力将抑制流体切线方向速度的变化，而且流体运动受壁面阻碍，从而抑制了正常的波动。

在近壁面的外部区域，湍流动能受平均流速的影响而增大，湍流运动加剧。LES模型仅适用于湍流核心区域（一般都远离壁面），应该考虑怎样使这些模型适用于壁面边界层处的流动。如果近壁面的网格划分足够好，Spalart-Allmaras和k-ω模型可以解决边界层的流动。

前面介绍的k-ε模型均为针对充分发展的湍流、高Re数的湍流模型，但对于近壁区的流动，Re数较低，湍流发展并不充分，湍流的脉动影响不如分子黏性的影响大。要对近壁区内的流动进行模拟计算，必须对前面所述的k-ε方程进行修正。壁面函数法和低Re数k-ε模型均可有效解决近壁区及低Re数情况下的流动计算问题。

在无滑移壁面附近存在很强的变量梯度，此时，黏性效应对运输过程有很大影响，在数值模拟过程中需考虑壁面的黏性效应和边界层内快速变化的变量的求解这两大问题。

研究表明，对于在固体壁面上充分发展的湍流流动，沿壁面法线方向可将流动区域划分为壁面区和核心区。核心区的流动可以认为是完全湍流区。壁面区又可分为黏性底层、过渡层和对数律层。

黏性底层在最里层，又叫黏性力层，流动区域很薄，在这个区域里，黏性力在动量、热量及质量交换中起主导作用，湍流切应力可以忽略，因此流动几乎是层流流动，平行于壁面的速度分量沿壁面法线方向呈线性分布。

过渡层处于黏性底层的外面，其中黏性力与湍流切应力的作用相当，流动状况比较复杂，很难用一个公式或定律来表述。由于过渡层的厚度极小，故计算中将其归入对数律层。

对数律层处于最外层，其中黏性力的影响不明显，湍流切应力占主导地位，流动处于充分发展的湍流状态，流速分布接近对数关系。

为了建立壁面函数，现引入两个无量纲参数u⁺和y⁺，分别表示速度和距离，即

式中 u——流体的时均速度；

u_τ——壁面摩擦速度，；(www.xing528.com)

τ_w——壁面切应力；

∆y——到壁面的距离。

大量实验表明，近壁面区域可以分成3层区域，如图1-3所示，以lny⁺为横坐标，u⁺为纵坐标，将壁面区内划分为3个子层及核心区内的流动。图1-3中的小三角形及小空心圆代表在两种Re数下实测得到的速度值u⁺，直线代表对速度进行拟合后的结果。

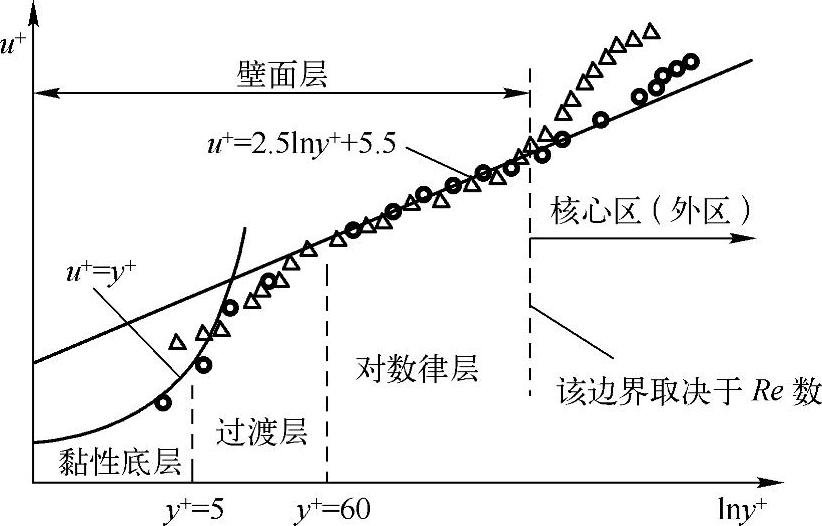
图1-3 璧面区3个子层的划分与相应的速度

根据普朗特的边界层理论，黏性较小的流体绕流物体时，黏性的影响仅限于贴近物面的薄层内，而在薄层之外可以忽略。在这个薄层内，形成一个从固体壁面速度为零到外流速度的速度梯度区，这一薄层即边界层。

合适的边界层网格分布是用好湍流模型的关键因素之一。边界层网格质量的控制可通过控制y⁺值范围来实现，一般对于壁面函数法，要求20＜y⁺＜100；对低雷诺数模型，要求y⁺＜2。根据要控制的y⁺值范围，可确定边界层内网格节点和壁面间的最小距离∆y，按式（1-17）确定。

式中 L——特征长度，单位为m；

Re——特征长度处对应的雷诺数。

假设近壁面的速度分布符合对数函数，可以在边界层内计算得出流体的剪切应力，该函数即壁面函数。通常，近壁面区域流动分析有两种方法：壁面函数法和低Re数k−ε模型法。