不对称跌落故障原因分析与解决方法

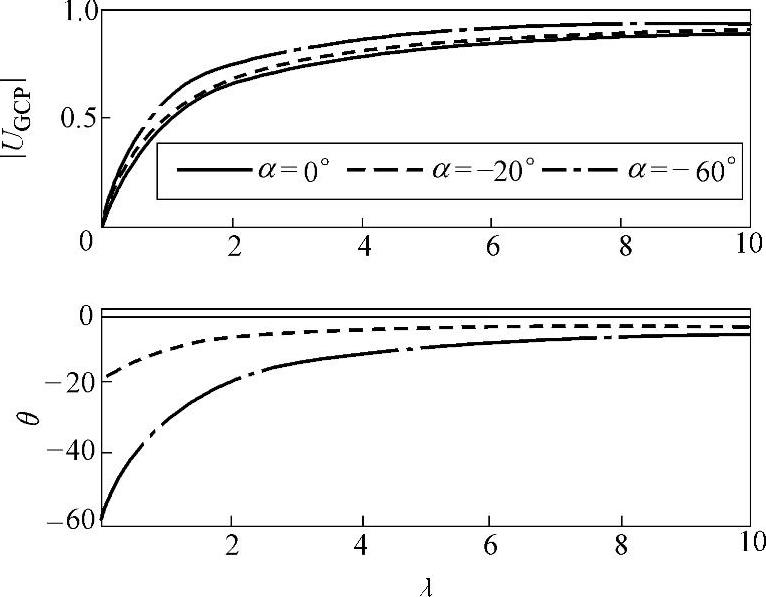
图9-3 三相短路故障下GCP点 电压幅值和相位跳变

不对称故障下，电网电压中会出现正序、负序和零序分量。由于图9-1中变压器T₁、T₂均采用Y/d联结，故障后零序电压被变压器隔离，不会传递到新能源发电系统的机端，因而以下分析中可不考虑零序分量。正序和负序电压分量对光伏发电系统或者风力发电系统的影响不同，因而下面采用对称分量法分别分析故障下电网电压的正序和负序电压分量的典型特征。为分析简单起见，令Z_s⁺≈Z_s^-≈Z⁰_s=Z_s，Z_f⁺≈Z_f-≈Z⁰_f=Z_f。式中，上标“+”“-”和“0”分别表征正序、负序和零序分量。

根据对称分量法，三相变量可由三组正负零序对称分量叠加而成。值得注意的是，传统的对称分量法是基于系统稳态的分析方法，分析时，三相电压、电流变量可用三相稳态相量表示。各序分量与三相变量的关系可由如下变换得到。

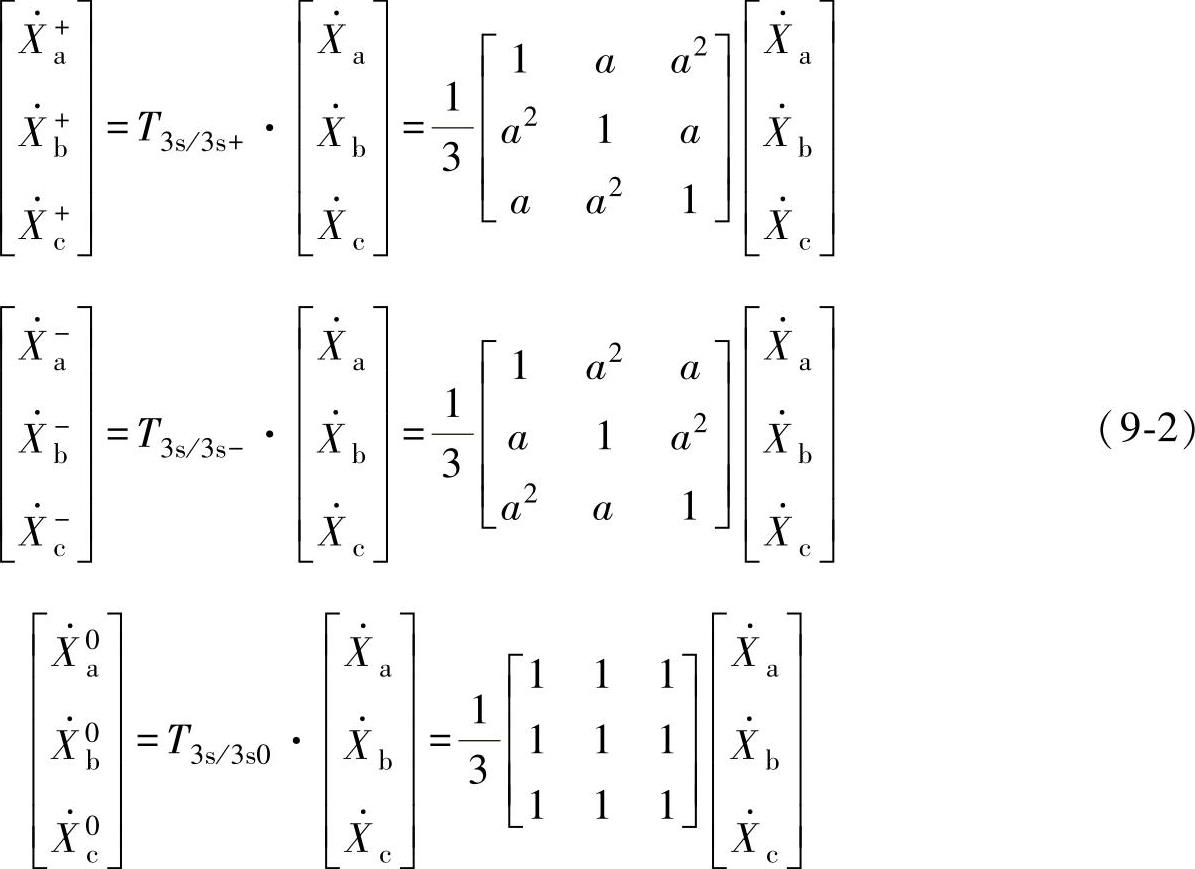
式中，a是120°相移算子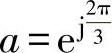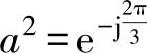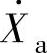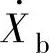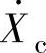，，；、、分别为三相电压或电流相量。

对于三相线性系统，可根据对称分量法，将三相不对称系统分为三组三相对称系统（正序、负序和零序）进行分析，再由叠加原理得到整个系统的特性。由对称分量法，图9-2所示分压模型可进一步表示为图9-4所示。图中电网电压u_gx（x=a，b，c）只含有正序分量，故障点电压u_fx（x=a，b，c）含正、负和零序分量，Z_sa=Z_sb=Z_sc=Z_s，Z_fa=Z_fb=Z_fc=Z_f。由对称分量法，图9-4所示系统各电压电流变量可由图9-5中三组对称系统的相应变量叠加而得。针对图9-5所示的三组三相对称系统，其特性可用图9-6所示单相稳态序网络来分析。

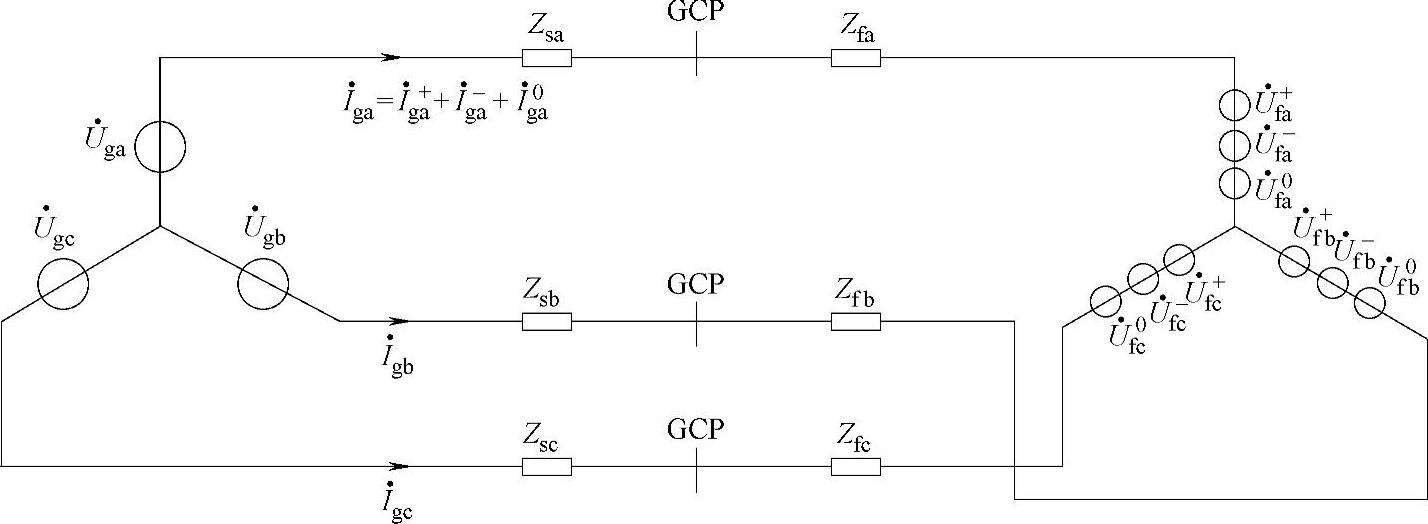
图9-4 电网故障的三相分压模型

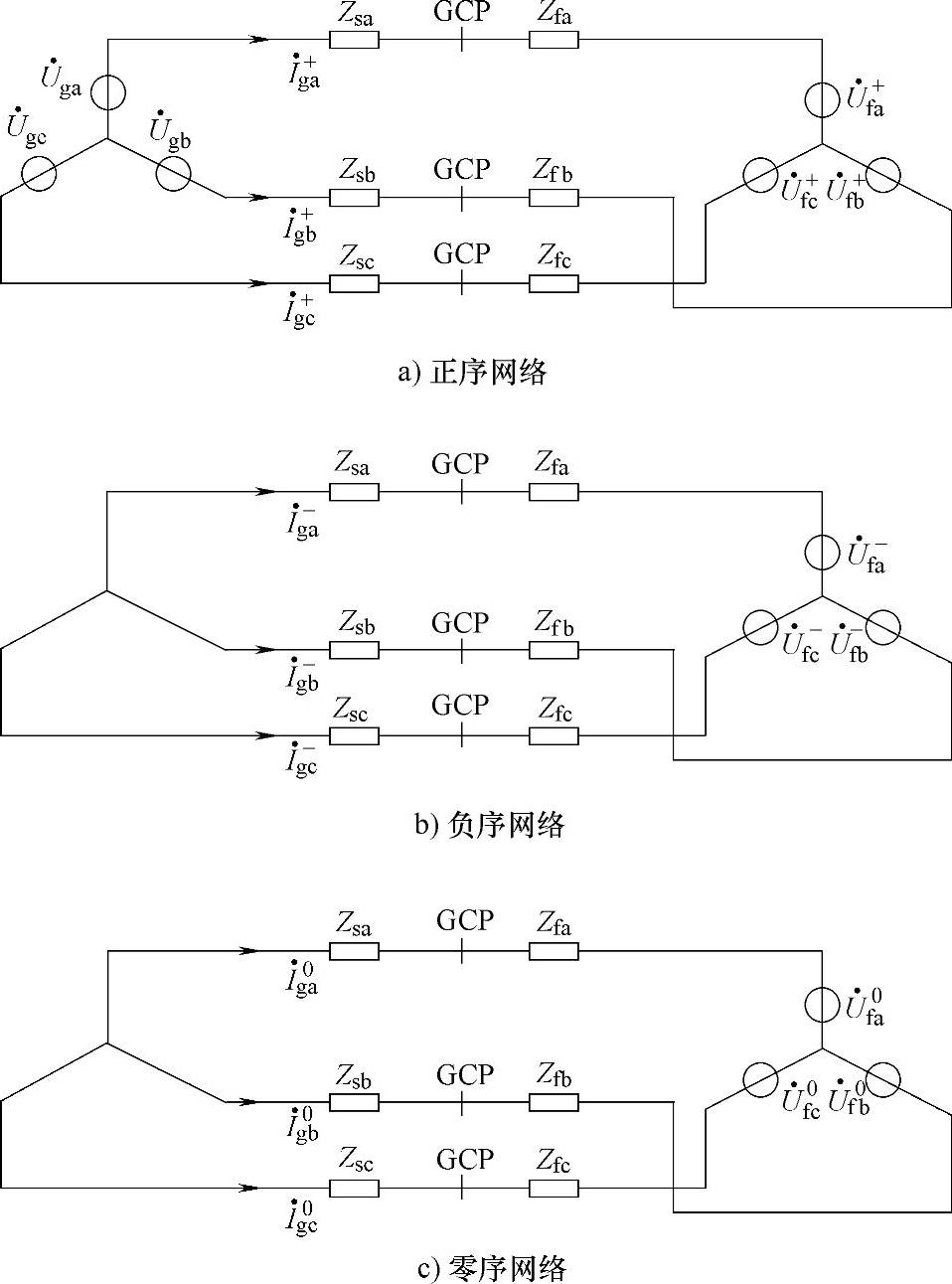
图9-5 分压模型的三相序网络

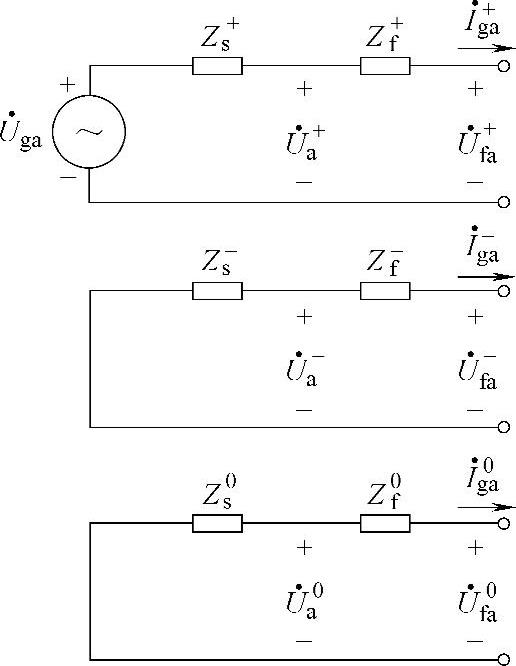
图9-6 三相对称系统的单相序网络

1.单相对地故障

假设故障发生在A相，忽略风场注入GCP的电流，此时b，c相开路（见图9-2），由图9-4可知：

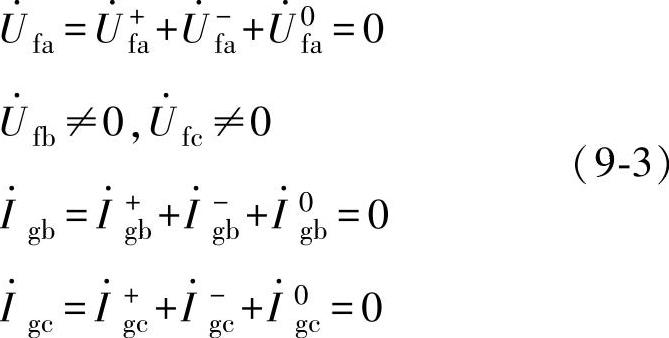
进一步，由式（9-2）可知，上式可整理为边界条件

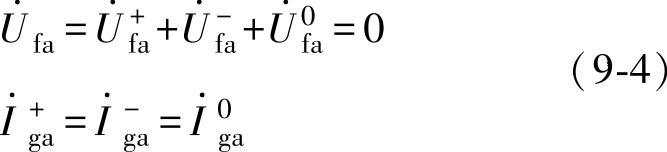
由边界条件式（9-4），单相对地故障可由图9-7所连接的复合序网络进行分析。

可知，GCP点的序电压分量分别为(www.xing528.com)

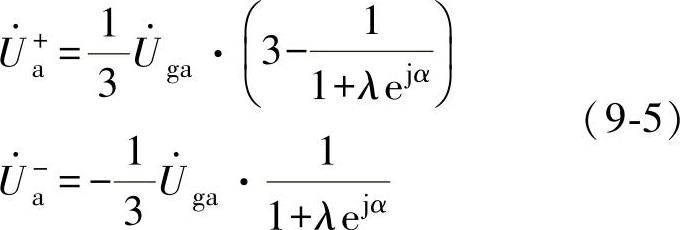
式中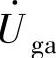，表示电网故障前的a相电压相量。由于存在Y/d联结变压器，零序分量无法传递到并网发电系统的机端，因而未在上述分析中列出。

故障后三相电压分量的瞬时值可由式（9-5）所示序电压分量和式（9-2）的逆变换求得。

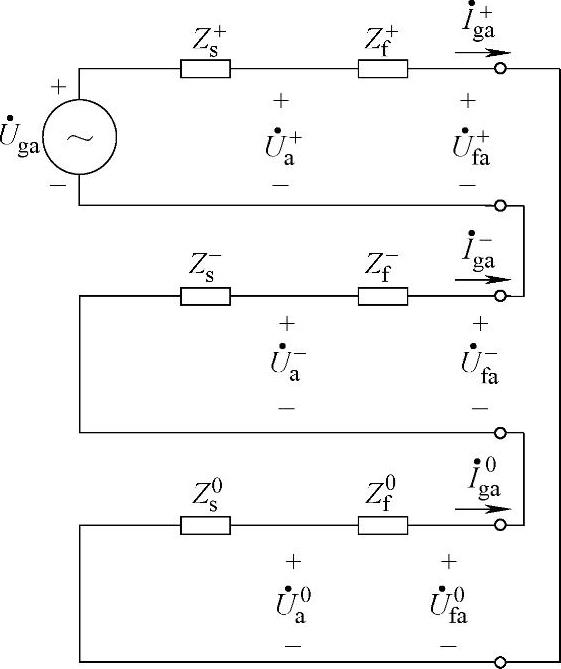
图9-7 单相接地故障的等效模型

2.相间短路故障

假设故障发生在B、C相，与单相对地故障的分析类似，可得序网络的连接如图9-8所示，同样可知GCP点的正负序电压分量分别如下：

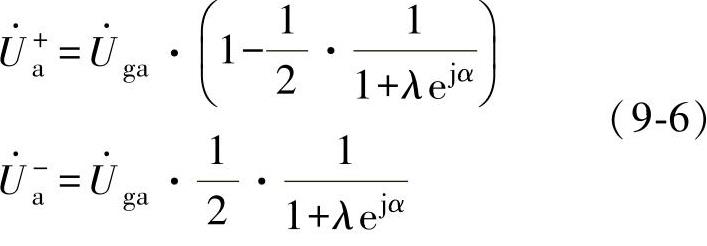
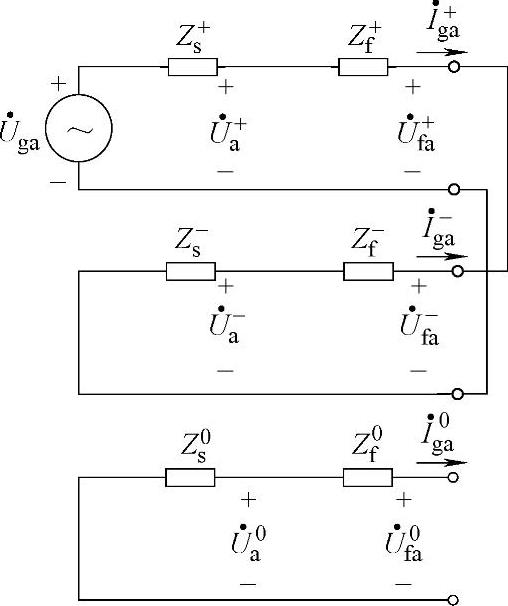
图9-8 相间短路故障的等效模型

3.两相接地故障

假设故障发生在B、C相和地之间，序网络的连接如图9-9所示，同样GCP的正负序电压分量分别如下：

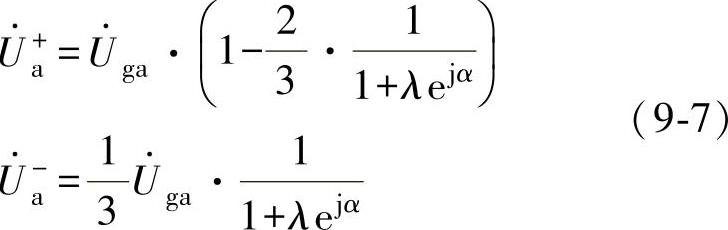
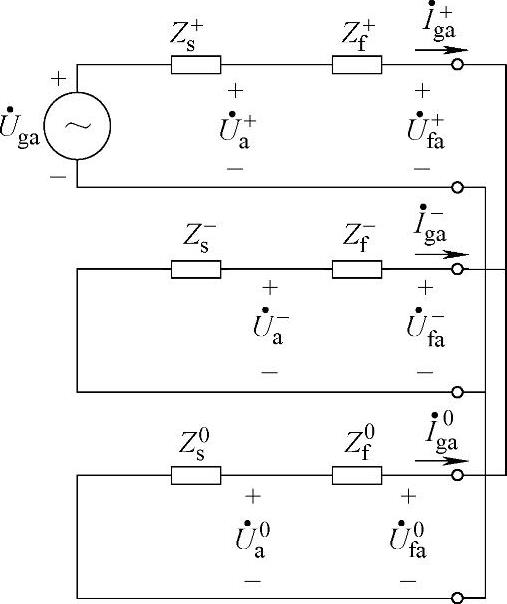
图9-9 两相接地故障的等效模型

根据式（9-5）～式（9-7），不同故障类型、不同阻抗角α下的序电压分量（“+，-”分别表示正序分量与负序分量）与λ的关系如图9-10所示，图中，φ为相位角跳变。可见，正序电压分量的跌落幅值随λ（故障距离）的增加而减小。相同故障距离下，三相对称故障引起的正序电压跌落最严重，而单相对地故障的影响最小，两相接地故障的情况比三相对称故障轻但比相间短路故障严重。若Z_s、Z_f的阻抗比（X/R）相同，则GCP电压故障前后不会出现相位角突变，若阻抗比不同，则故障后会出现相位角突变，且相位角差随着故障距离的增加而减小，最大相位角差取决于阻抗角α或电网结构。不对称故障下，GCP电压含有负序分量，然而其最大值不会超过0.5pu。若进一步考虑输电线和变压器阻抗的影响，发电系统的负序电压分量将会更小。随着故障距离的增加，负序电压分量的幅值不断减小。相同故障距离条件下，单相接地故障和两相接地故障产生相同的负序电压分量。与单相接地和两相接地故障相比，相间故障引起的负序分量最大，对某些结构的新能源并网发电系统，如半耦合型风电系统，其危害较大，将成为LVRT最难的一种故障类型。若α=0°，两相接地或相位角短路故障后，负序电压分量无相位角突变，单相接地故障则会引起-180°的相移。若α≠0°，负序电压的相位角突变随着故障距离的增加而增大，同样，其最大值取决于α。

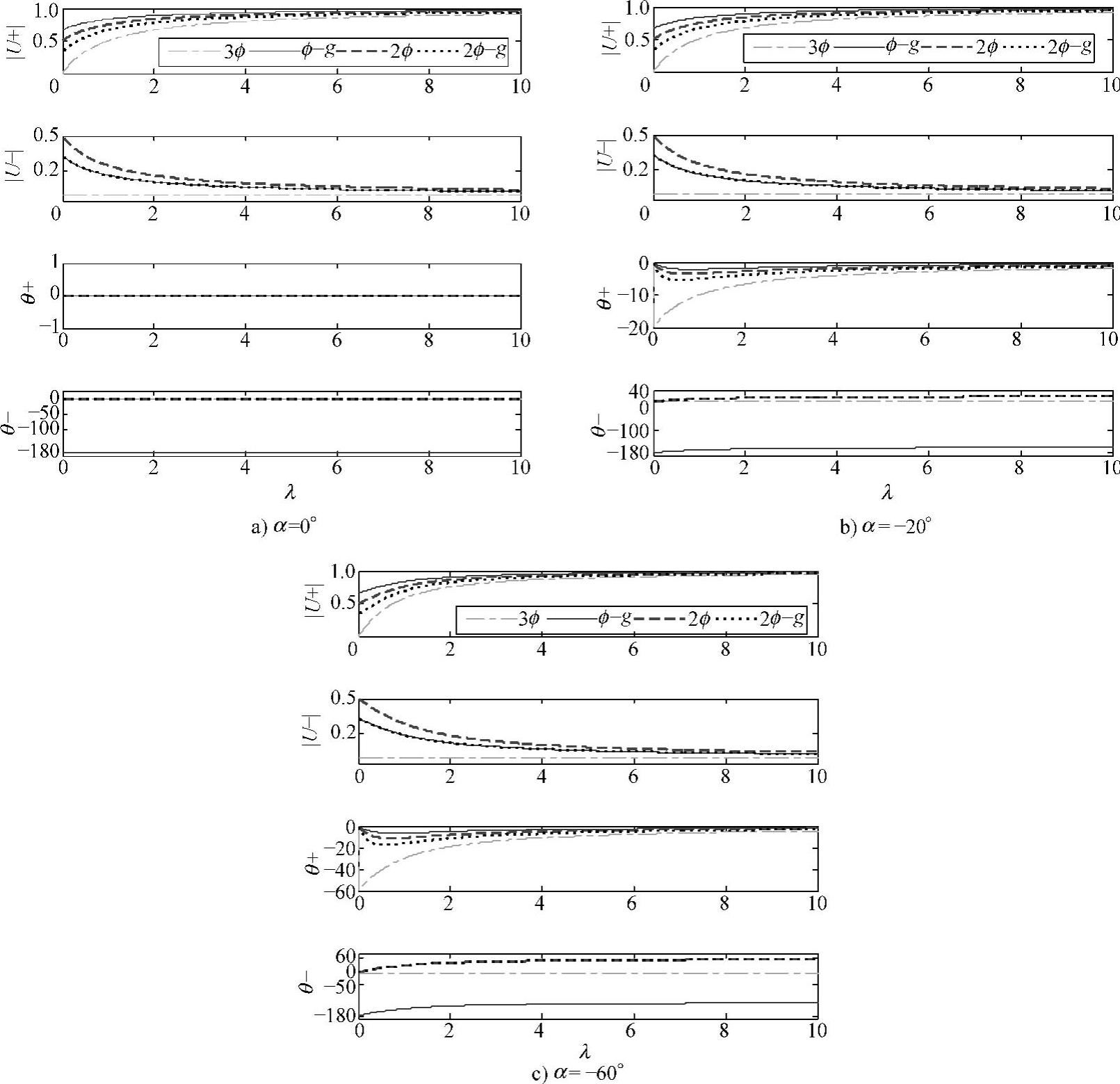
图9-10 不同故障类型和距离下的序电压幅值及相位跳变